これまで,離散フーリエ変換(DFT)について紹介してきました。DFTは,信号に含まれる振動成分を周波数ごとに分解するというものでした(これまでに,テスト信号,音声信号の振幅スペクトルを表示する方法を紹介しました)。
それでは,信号に含まれる周波数や振幅が時間的に変化する場合はどうでしょうか。
例えば「こんにちは」という音声データの解析をするときには,最初の「こ」と二番目の「ん」に含まれている振動成分は異なるだろうと考えるのは自然です(だから人間は「こ」と「ん」を区別できているのです)。
これまで紹介してきたようなDFTの解析・操作では,時間的に変化する信号に対して,全体にフーリエ変換をかけてしまい,「こ」と「ん」に含まれる成分が混ざった振幅スペクトルが得られてしまいます。
この問題を解決するために,瞬間瞬間に(とはいってもある時間的な広がりを持って)DFTを施して,その瞬間の周波数成分を解析する手法を短時間フーリエ変換(Short Time Fourier Transform: STFT)といいます。
STFTを用いれば,振動数や振幅が時間とともに変化する信号に対して,「どの時刻にどのくらいの周波数成分がどれほど強いか」という情報が得られ,適切な解析をすることができます。
本記事では,STFTによって得られるスペクトログラム (spectrogram) を表示するPythonのプログラムを作成することを目標にします。
スペクトログラムはどの時間にどの周波数帯の信号が強いかを表す図のことです。
スペクトログラムを表示するには,scipyやpydubを使うのが手っ取り早いですが,原理を理解するためにも,これらを使わない方法について説明します。
一度理解すれば,scipyやpydubで用意されているものを使用する際にも,引数が何を意味するのかを理解する助けになると思います。
macOS Big Sur, python3.7.9, pydub0.25.1

Pythonを使ってスペクトログラムを作成する方法
STFTの手順(スペクトログラムを得る手順)
ある時系列信号を考えます。この信号の変化に対して,ある短い時間幅を設定します。時間幅を切り出す関数を窓関数 (window function) といいます。
STFTは,解析したい初期時刻 $t_1$ (の周辺)に窓関数をかけて時間を切り出し,その時間内でDFTを行い,次の時刻 $t_2$ に窓関数をかけて時間を切り出し,その時間内でDFTを行い,次の…という操作を解析したい時間全体で繰り返し行うものです。
こうすることで各時刻において,信号のスペクトルが得られ,それを時間方向に並べることで時間に対するスペクトルの変化を追うことができます。
STFTは以上の内容をプログラムに落とし込めば完成です!
STFTの実装
「ある時間幅を決めて,DFTを繰り返しかける」とは言うものの,これだけではやり方は一意に決まりません。
私がよくやるのは,解析したい信号が決まったら,窓関数の時間幅と t_wndw と解析対象時間内で何回STFTを行うかというパラメータ n_sftf を与えるやり方です (scipyやpydubでは窓関数と窓関数のオーバラップを指定するという方法が取られます)。
t_wndw は「解析したい信号がどのくらいの時間スケールで変化しているか」と「ほしい周波数の分解能」考慮して,長すぎず,短すぎずにならないように選びます。急激に信号(の振幅や振動数)が変化する場合は t_wndwとして短い値を設定し,n_stftを多めにすると急激な時間変化を追うことができます。ただし,この場合,周波数分解能は悪くなるので注意が必要です。
t_wndwを長くすると周波数分解能が高くなりますが,t_wndw間での周波数の変化を追うことはできません。
スペクトログラム
スペクトログラムは横軸に時間を,縦軸に周波数をとり,振幅スペクトル(またはパワースペクトル)を第3軸にとって,色または高さで表示した図のことです。
第3軸のスペクトルは値が大きく変化します(し,音声データでは特にdBが使われることが多い)ので,対数のスケールで表示されることが多いです。
前置きが長くなりましたが,Pythonで実装したものが下のコードです。
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.patheffects as path_effects
import numpy as np
from pydub import AudioSegment
#------------------------------------------------------------------------------
# ボイスメモで収録したm4aファイルを読み込む
sounds = AudioSegment.from_file('aiueo.m4a', 'm4a')
print(f'channel: {sounds.channels}')
print(f'frame rate: {sounds.frame_rate}')
print(f'duration: {sounds.duration_seconds} s')
# チャンネルが2(ステレオ) の場合,L/R交互にデータが入っているので,二つおきに読み出す。
sig = np.array(sounds.get_array_of_samples())[::sounds.channels]
dt = 1.0/sounds.frame_rate # サンプリング時間
tms = 0.0
tme = sounds.duration_seconds # サンプル終了時刻
tm = np.linspace(tms, tme, len(sig), endpoint=False) # 時間ndarrayを作成
#------------------------------------------------------------------------------
# ウィンドウ幅,STFTを施す数の設定
t_wndw = 100.0e-3 # 100 milisecond
n_stft = 100 # number of STFT
freq_upper = 2.0e3 # 表示する周波数の上限
out_fig_path = "spectrogram.png" # 出力ファイル名(path)
#------------------------------------------------------------------------------
# 短時間フーリエ変換
# 時間刻み
dt = tm[1] - tm[0]
# 入力された n_wndw を t_wndwで設定した幅より小さい,かつ,2の累乗個に設定する
n_wndw = int(2**(np.floor(np.log2(t_wndw/dt))))
t_wndw = n_wndw*dt # recalculate t_wndw
n_freq = n_wndw
# 周波数
freq_sp = np.fft.fftfreq(n_wndw, dt)
# スペクトルを計算する時刻を決める
m = len(tm) - n_wndw
indxs = np.zeros(n_stft, dtype=int)
for i in range(n_stft):
indxs[i] = int(m/(n_stft+1)*(i+1)) + n_wndw//2
tm_sp = tm[indxs] # DFTをかける時刻の配列
# スペクトログラムを計算する
# スペクトルは indxs[i] - n_wndw //2 + 1 ~ indxs[i] + n_wndw//2 の n_wndw 幅で行う
sp = np.zeros((n_freq, n_stft), dtype=complex) # スペクトログラムの2次元ndarray
wndw = np.hamming(n_wndw) # hamming窓
#wndw = np.hanning(n_wndw) # hanning窓
#wndw = np.ones(n_wndw) # 矩形窓
for i in range(n_stft):
indx = indxs[i] - n_wndw//2 + 1
sp[:, i] = np.fft.fft(wndw*sig[indx:indx+n_wndw], n_wndw)/np.sqrt(n_wndw)
#------------------------------------------------------------------------------
# 解析結果の可視化
figsize = (210/25.4, 294/25.4)
dpi = 200
fig = plt.figure(figsize=figsize, dpi=dpi)
# --- 図の設定 (全体)
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['xtick.top'] = True
plt.rcParams['xtick.major.size'] = 6
plt.rcParams['xtick.minor.size'] = 3
plt.rcParams['xtick.minor.visible'] = True
plt.rcParams['ytick.direction'] = 'in'
plt.rcParams['ytick.right'] = True
plt.rcParams['ytick.major.size'] = 6
plt.rcParams['ytick.minor.size'] = 3
plt.rcParams['ytick.minor.visible'] = True
plt.rcParams["font.size"] = 14
plt.rcParams['font.family'] = 'Helvetica'
# 窓関数幅をプロット上部に記載
fig.text(0.10, 0.95, f't_wndw = {t_wndw} s, ')
# プロット枠 (axes) の設定
ax1 = fig.add_axes([0.15, 0.55, 0.70, 0.3])
ax_sp1 = fig.add_axes([0.15, 0.2, 0.70, 0.30])
cb_sp1 = fig.add_axes([0.87, 0.2, 0.02, 0.30])
# 元データのプロット
ax1.set_xlim(tms, tme)
ax1.set_xlabel('')
ax1.tick_params(labelbottom=False)
ax1.set_ylabel('x')
ax1.plot(tm, sig, c='black')
# スペクトログラムのプロット
ax_sp1.set_xlim(tms, tme)
ax_sp1.set_xlabel('time (s)')
ax_sp1.tick_params(labelbottom=True)
ax_sp1.set_ylim(0, freq_upper)
ax_sp1.set_ylabel('frequency\n(Hz)')
norm = mpl.colors.Normalize(vmin=np.log10(np.abs(sp[freq_sp < freq_upper, :])**2).min(),
vmax=np.log10(np.abs(sp[freq_sp < freq_upper, :])**2).max())
cmap = mpl.cm.jet
ax_sp1.contourf(tm_sp, freq_sp, np.log10(np.abs(sp)**2),
norm=norm,
levels=256,
cmap=cmap)
ax_sp1.text(0.99, 0.97, "spectrogram", color='white', ha='right', va='top',
path_effects=[path_effects.Stroke(linewidth=2, foreground='black'),
path_effects.Normal()],
transform=ax_sp1.transAxes)
mpl.colorbar.ColorbarBase(cb_sp1, cmap=cmap,
norm=norm,
orientation="vertical",
label='$\log_{10}|X/N|^2$')
# 図を保存
plt.savefig(out_fig_path, transparent=False)窓関数の種類
DFTは,窓関数で切り出した信号が後にも先にも繰り返されている,としてスペクトルを算出します。
したがって,窓関数の端では信号は「いびつな」または「不自然に」つながってしてしまうことになります。これはDFTで得られるスペクトルを歪ませてしまう原因となります。
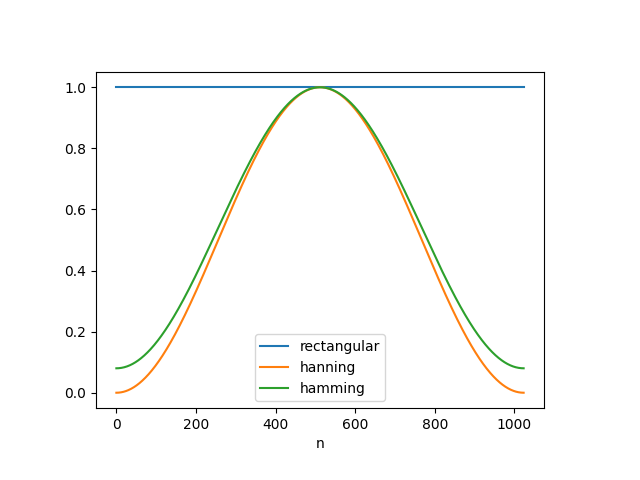
この問題を解決するために,最もナイーブな矩形窓を窓関数として用いるのではなく,窓関数の端で0に近づける窓関数が提案されています。いくつか代表的なものとその波形を挙げておきます。
コード解説で詳しく述べますが,これを実装するのは簡単でnumpyの関数がすでに用意されています。
- 矩形窓$$ w(n) = 1, \quad n = 0, 1, 2, \dots, N-1 $$
- hanning窓$$ w(n) = 0.5 – 0.5\cos\left(\frac{2\pi n}{N-1}\right), \quad n = 0, 1, 2, \dots, N-1 $$
- hamming窓$$ w(n) = 0.54 – 0.46\cos\left(\frac{2\pi n}{N-1}\right), \quad n = 0, 1, 2, \dots, N-1 $$
実際にコードを実行してみよう
上で記述したコードはstft-demo.pyという名前のファイルとして,音声データファイルと同じディレクトリ(ここでは~/Desktop/LabCode/python/stftとします)に保存します。
ターミナルを開き,
$ cd ~/Desktop/LabCode/python/stftと入力し,ディレクトリを移動します。あとは以下のコマンドで stft-demo.pyを実行するだけです。( $マークは無視してください)。
$ python3 stft-demo.py実行結果
「あいうえお」と喋った音声の場合
上のプログラムを実行すると,プログラムを保存したディレクトリにspectrogram.pngというファイルができているはずです。
私は,「あいうえお」とゆっくり喋った音声ファイルを入力としたので,したのような結果が得られました。
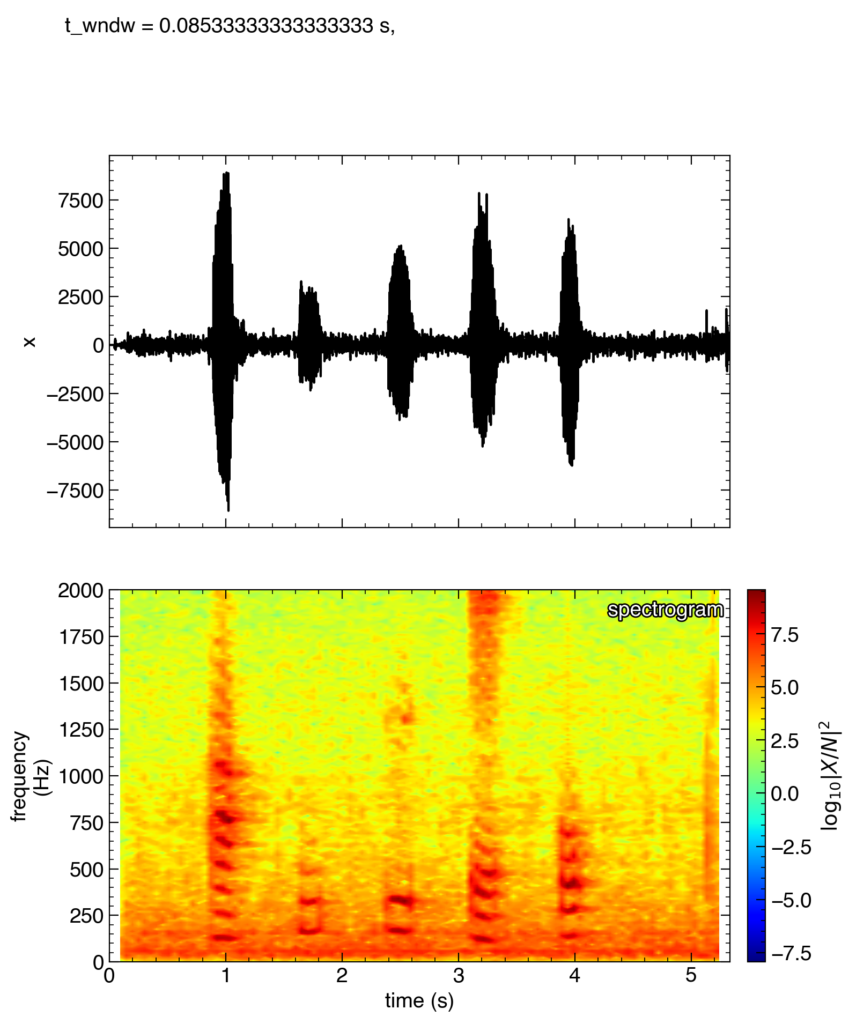
一段目は生データ,二段目はスペクトログラムを表示しています。
スペクトログラムは縦軸に周波数,横軸に時間,そして第3軸(高さや色で表現)に振幅スペクトルやパワースペクトルを表示したものです。赤色になっている部分は振幅スペクトルが大きいところで,その時間にその周波数の成分が多く含まれていることを示しています。
スペクトログラムに注目すると,「あ」,「い」,「う」,「え」,「お」に対応する時刻に赤い水平の筋が縦に並んだものが見えます。「あ」対応する1秒付近に現れるパターンと,「お」に対応する4秒付近に現れるパターンには違いが見られます。また,無音時にはパターンは見られません。
声の高さを変えて「あ〜〜〜〜」と喋った音声の場合
つぎに,入力ファイルを,声の高さを変えて「あ〜〜〜〜」と喋ったものにしてみました。
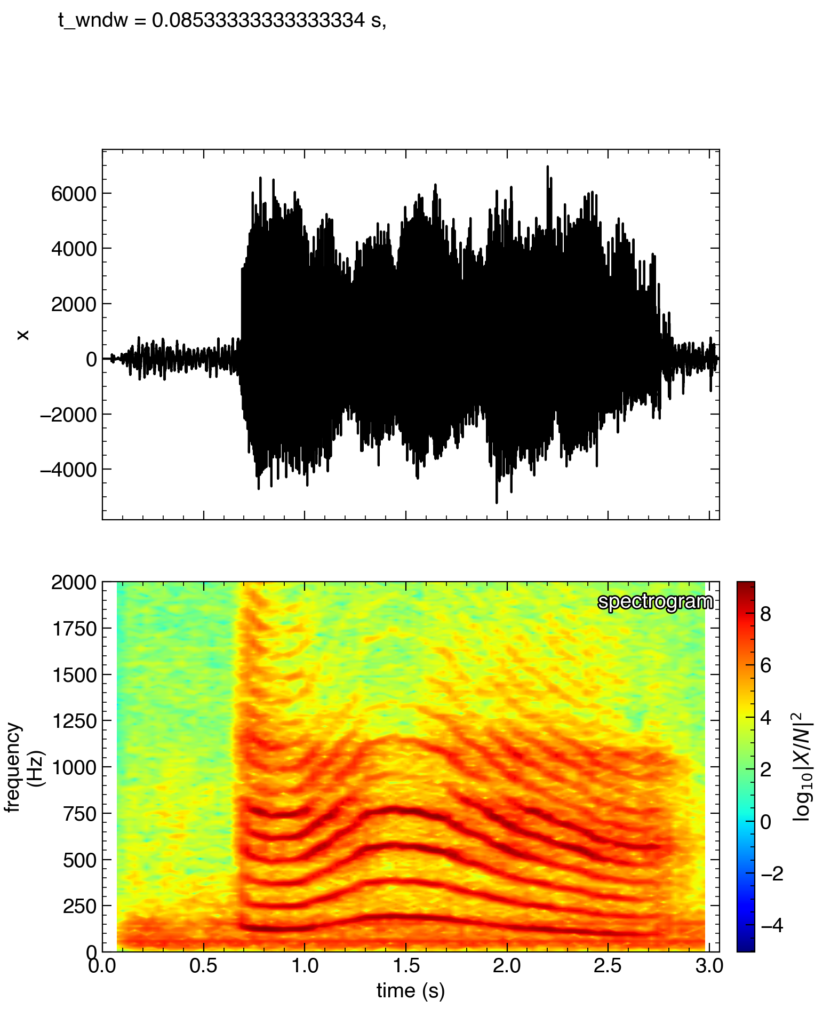
出力結果が上の図です。
二段目を見ると1.5秒付近で声の高さがピーク(はじめ基本波で150Hzだったものが,250Hzくらい)になっている事がわかります。実際に聞いてみると(非常に滑稽な音声ですが…)たしかに,1.5秒付近で声の高さがmaxになっていました。
また,全体を一回のDFTで解析すると得られない周波数の時間変化を可視化することに成功しています!!
コードの解説
作成したコードの解説をしていきます。
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.patheffects as path_effects
import numpy as np
from pydub import AudioSegmentモジュールをインポートします。
#------------------------------------------------------------------------------
# ボイスメモで収録したm4aファイルを読み込む
sounds = AudioSegment.from_file('aiueo.m4a', 'm4a')
print(f'channel: {sounds.channels}')
print(f'frame rate: {sounds.frame_rate}')
print(f'duration: {sounds.duration_seconds} s')
# チャンネルが2(ステレオ) の場合,L/R交互にデータが入っているので,二つおきに読み出す。
sig = np.array(sounds.get_array_of_samples())[::sounds.channels]
dt = 1.0/sounds.frame_rate # サンプリング時間
tms = 0.0
tme = sounds.duration_seconds # サンプル終了時刻
tm = np.linspace(tms, tme, len(sig), endpoint=False) # 時間ndarrayを作成音声ファイル(ボイスメモで録音した声のファイル)を読み込みます。ここでは,「aiueo.m4a」という拡張子m4aの音声ファイルを読み込むことを想定しています。音声ファイル名や拡張子はご自身のファイル合わせて変更してください。numpy配列に変換し,時間のnumpyアレイも作成します。
#------------------------------------------------------------------------------
# ウィンドウ幅,STFTを施す数の設定
t_wndw = 100.0e-3 # 100 milisecond
n_stft = 100 # number of STFT
freq_upper = 2.0e3 # 表示する周波数の上限
out_fig_path = "spectrogram.png" #出力ファイル名(path)STFTのウィンドウ幅と全時間帯で何回STFTを施すかを設定します。また,表示する周波数の上限と出力ファイル名(ファイルパス)を与えます。
#------------------------------------------------------------------------------
# 短時間フーリエ変換
# 時間刻み
dt = tm[1] - tm[0]
# 入力された n_wndw を t_wndwで設定した幅より小さい,かつ,2の累乗個に設定する
n_wndw = int(2**(np.floor(np.log2(t_wndw/dt))))
t_wndw = n_wndw*dt # recalculate t_wndw
n_freq = n_wndw
# 周波数
freq_sp = np.fft.fftfreq(n_wndw, dt)
# スペクトルを計算する時刻を決める
m = len(tm) - n_wndw
indxs = np.zeros(n_stft, dtype=int)
for i in range(n_stft):
indxs[i] = int(m/(n_stft+1)*(i+1)) + n_wndw//2
tm_sp = tm[indxs] # DFTをかける時刻の配列
# スペクトログラムを計算する
# スペクトルは indxs[i] - n_wndw //2 + 1 ~ indxs[i] + n_wndw//2 の n_wndw 幅で行う
sp = np.zeros((n_freq, n_stft), dtype=complex) # スペクトログラムの2次元ndarray
wndw = np.hamming(n_wndw) # hamming窓
#wndw = np.hanning(n_wndw) # hanning窓
#wndw = np.ones(n_wndw) # 矩形窓
for i in range(n_stft):
indx = indxs[i] - n_wndw//2 + 1
sp[:, i] = np.fft.fft(wndw*sig[indx:indx+n_wndw], n_wndw)/np.sqrt(n_wndw)STFTを行います。まず,FFTアルゴリズムを使用する時はデータ数を2の累乗個にするのが約束(このあたりはこれまで曖昧にしてきました。少なくともnumpy.fftを使用すると,データ数が2の累乗個でなかったとしても0パディングなどの操作が行われ,2の累乗個になります。今回は明示的に2の累乗個にしておきます)なので,n_wndw*dtが与えたt_windwを上回らない,2の累乗個で表される(n_windw = 1, 2, 4, 8, 16…)最も大きなn_wndwを選択します。
長さn_wndw,時間幅dtの時系列データをDFTした時の周波数列をnp.fft.fftfreqでもらいます。
次に,スペクトルを計算する時刻を決めます。全時間帯tms ~ tmeでn_stft回だけDFTを均等幅で行うには,どの時刻を中心としてDFTを行えばよいかを計算します。DFTを行うべき時刻のインデックスをindexsという配列に格納します。
あとはspというスペクトログラムを格納する2次元のnumpy配列を用意して,先程得た時刻の周りでDFTをn_stft回実行するだけです。スペクトル歪みの問題があるため,窓関数をかけて実行します。今回はhamming窓を使用しました。
#------------------------------------------------------------------------------
# 解析結果の可視化
figsize = (210/25.4, 294/25.4)
dpi = 200
fig = plt.figure(figsize=figsize, dpi=dpi)
# --- 図の設定 (全体)
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['xtick.top'] = True
plt.rcParams['xtick.major.size'] = 6
plt.rcParams['xtick.minor.size'] = 3
plt.rcParams['xtick.minor.visible'] = True
plt.rcParams['ytick.direction'] = 'in'
plt.rcParams['ytick.right'] = True
plt.rcParams['ytick.major.size'] = 6
plt.rcParams['ytick.minor.size'] = 3
plt.rcParams['ytick.minor.visible'] = True
plt.rcParams["font.size"] = 14
plt.rcParams['font.family'] = 'Helvetica'
# 窓関数幅をプロット上部に記載
fig.text(0.10, 0.95, f't_wndw = {t_wndw} s, ')解析結果の可視化を行います。今回はこれまでと違って,A4用紙に出力することを想定してpngファイルを出力することにします。
figsizeで指定しているのは縦置きのA4用紙サイズ,dpiは解像度です。
また,論文などで使用するのに堪える図を出力することを想定して,ティックの設定(内側に,上にも右にも同じもの,サイズを大きく)やフォントの設定を変更します。
窓関数幅は重要なパラメータなので,図の上に記載するようにしました。
# プロット枠 (axes) の設定
ax1 = fig.add_axes([0.15, 0.55, 0.70, 0.3])
ax_sp1 = fig.add_axes([0.15, 0.2, 0.70, 0.30])
cb_sp1 = fig.add_axes([0.87, 0.2, 0.02, 0.30])
# 元データのプロット
ax1.set_xlim(tms, tme)
ax1.set_xlabel('')
ax1.tick_params(labelbottom=False)
ax1.set_ylabel('x')
ax1.plot(tm, sig, c='black')
# スペクトログラムのプロット
ax_sp1.set_xlim(tms, tme)
ax_sp1.set_xlabel('time (s)')
ax_sp1.tick_params(labelbottom=True)
ax_sp1.set_ylim(0, freq_upper)
ax_sp1.set_ylabel('frequency\n(Hz)')
norm = mpl.colors.Normalize(vmin=np.log10(np.abs(sp[freq_sp < freq_upper, :])**2).min(),
vmax=np.log10(np.abs(sp[freq_sp < freq_upper, :])**2).max())
cmap = mpl.cm.jet
ax_sp1.contourf(tm_sp, freq_sp, np.log10(np.abs(sp)**2),
norm=norm,
levels=256,
cmap=cmap)
ax_sp1.text(0.99, 0.97, "spectrogram", color='white', ha='right', va='top',
path_effects=[path_effects.Stroke(linewidth=2, foreground='black'),
path_effects.Normal()],
transform=ax_sp1.transAxes)
mpl.colorbar.ColorbarBase(cb_sp1, cmap=cmap,
norm=norm,
orientation="vertical",
label='$\log_{10}|X/N|^2$')
# 図を保存
plt.savefig(out_fig_path, transparent=False)プロット枠を設定し,データをプロットします。カラーバーの位置や大きさも自由に変えられるように明示的に設定しておきます。
まず元データのプロットしています。これには多言を要しないでしょう。
次に,スペクトログラムですが,これはcontourfを使ってプロットしています。normやcmapを変えると3軸目に対応するカラーの上限や下限,カラーマップを変更することができます。プロット枠の右上の白抜きのspectrogramの文字はpath_effectsを使います。このようにカラープロットの上に文字を表示する際には白抜きの文字を使用すると見やすくなり,便利です。
次に、スペクトログラムに表示されたカラーがどの値に対応するかを示すカラーバーを作成します。
最後に図を保存します。今回は非透過pngとするので,transparent=Falseとしておきます(デフォルトではFalseなので不要ですが,透過pngのほうが便利なこともあるので,あえて残しておきます)。
最後に
今回は,STFTを紹介しました。音声データを例にとって,時間的に振幅や周波数が変化するデータを解析し,スペクトログラムを表示して可視化してみました。
次回は,2つの信号中に含まれる振動成分の相関を測る指標である,「クロススペクトル」と「コヒーレンス」,そして,その間の位相差を測る「フェイズ」について説明します。




