これまで,フーリエ変換,ウェーブレット変換といった時間周波数解析の手法を紹介してきました。今回は,これまでとは少し毛色の変わった手法を紹介します。
特異スペクトル解析 (Singular Spectrum Analysis: SSA) は、時系列データなどからトレンド成分や周期的的な成分,ノイズ成分を抽出することができる手法です。非定常信号の解析に向いています。
macOS Monterey 12.6.2, Python 3.9.15, matplotlib 3.6.1, numpy 1.23.4, scipy 1.9.3

時系列データの特異スペクトル解析
特異値分解
まず,特異スペクトル解析で用いられる特異値分解について説明します。線形代数の言葉が出てきますので,難しいと思う方は飛ばしてもらっても大丈夫です。
階数 $r$ の $m\times n$ 行列 $\mathsf{A}$ に対して,次のような分解 (特異値分解 (singular value decomposition: SVD)といいます) が存在します:
$$
\mathsf{A} = \mathsf{U}\mathsf{\Sigma} \mathsf{V}^\top
$$
ここに,$\mathsf{U}$ と $\mathsf{V}$ はそれぞれ,$m$ 次と $n$ 次の直交行列 (複素行列の場合は,エルミート行列) で,$\mathsf{\Sigma}$ は
$$
\mathsf{\Sigma}
= \left(\begin{array}{cc}
\mathrm{diag}(\sigma_1, \sigma_2, \dots, \sigma_r) & \mathsf{O}_{r, n-r} \\
\mathsf{O}_{m-r, r} & \mathsf{O}_{m-r, n-r}\end{array}\right),
$$
$$
\sigma_1\ge \sigma_2\ge\cdots \ge \sigma_r > 0
$$
です。$\mathrm{diag}(\cdot)$ は対角成分が引数で表された対角行列を表し,$\mathsf{O}_{r, n-r}$ などは $r\times (n-r)$ 次の零行列を表します。難しく書きましたが,要するに,対角成分に $\sigma_1, \sigma_2,\dots, \sigma_r$ が並び,残りの成分は 0 の$m\times n$ 行列です。$\sigma_1, \sigma_2,\dots, \sigma_r$ は行列 $\mathsf{A}$ の特異値 (singular value) と呼ばれます。
なぜ,これが分解と呼ばれるかというと
$$
\mathsf{A} = \sigma_1 \mathbf{u}_1 \mathbf{v}_1^\top + \sigma_2\mathbf{u}_2\mathbf{v}_2^\top + \cdots + \sigma_r\mathbf{u}_r\mathbf{v}_r^\top
$$
と書くことができ,行列 $\mathsf{A}$ を「基底」 $\mathbf{u}_i\mathbf{v}_i^\top$で分解しているとみなせるからです。和を取るときの重みが特異値に対応し,どの基底が重要であるかを決めます。
特異値は $\sigma_1\ge \sigma_2\ge\cdots \ge \sigma_r > 0$ としていましたから,特異値の大きなものだけを足し合わせれば,だいたい $\mathsf{A}$ に近いものが出来上がります。すなわち,$\mathsf{A}$ を近似することができます。
時系列データの特異スペクトル解析
(以下では,python での実装を見据えて,0から始まる添字の付け方で説明しています。)
長さ $N$ の時系列データ $x_0, x_1, x_2, \dots, x_{N-1}$ を考えます。
特異スペクトル解析を行うには,まず,窓の幅 $K\ (< N)$ を定め,窓をずらしながら時系列データを切り出し,軌道行列 (trajectory matrix)と呼ばれる次の形の行列を作ります。
$$
\mathsf{X} = \left(\begin{array}{ccc}
x_0 & x_1 & x_2 & \cdots & x_{K-1} \\
x_1 & x_2 & x_3 & \cdots & x_{K} \\
x_2 & x_3 & x_4 & \cdots & x_{K+1} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
x_{L-1} & x_L & x_{L+1} & \dots & x_{N-1}
\end{array}\right)
$$
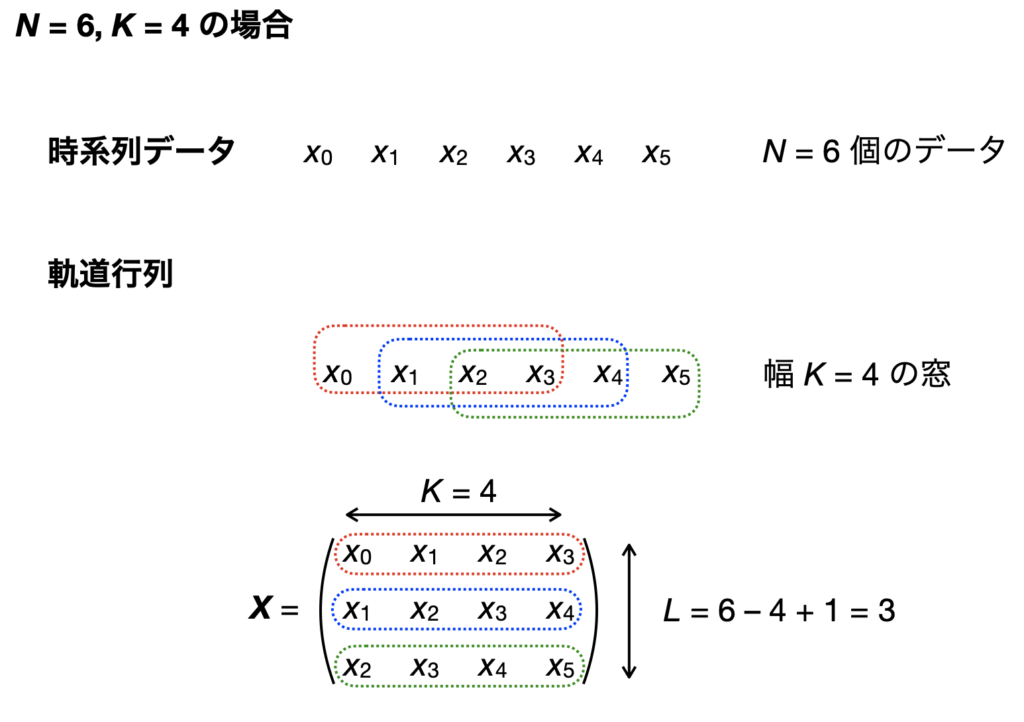
一行目は $x_0$ から $x_{K-1}$ までの $K$ 個のデータを,二行目は $x_1$ から $x_K$ までの $K$ 個のデータを,三行目は $x_2$ から $x_K+1$ までの $K$ 個のデータを,・・・というように,窓の右端が時系列データの右端 $x_{N-1}$ に到達するまで,つまり,$L = N -K + 1$ 回繰り返して並べたものです。
軌道行列を眺めると,右上から左下に向かって同じ成分が並んでいます。このような性質をもつ行列は Hankel (ハンケル) 行列と呼ばれます。
$N = 6$,$K=4$ の場合を図に示します。
つぎに,この行列に対して,上で述べた特異値分解を施します。
特異値分解を施すと,軌道行列が分解され,主要な成分については,その特異値が大きな値を持ちます。
分解されたもののうち,残しておきたい成分だけを残して,再構成します。例えば,ノイズ除去をしたい場合には,特異値の大きさを見て,ある閾値以上のものを残す等が考えられます。
$\mathsf{\Sigma}$ の対角成分に並んだ特異値のうち,残しておきたい成分だけを残し,他を0にしたものを $\widetilde{\mathsf{\Sigma}}$ とします。これを用いて,再構成された軌道行列を $\widetilde{\mathsf{X}}$と書くことにします。すなわち,次のようにします。
$$
\widetilde{\mathsf{X}} = \mathsf{U}\widetilde{\mathsf{\Sigma}}\mathsf{V}^\top
$$
diagonal averaging
元のデータを再構成には,diagonal averaging と呼ばれる操作が用いられます。式で書くと難しいのですが,要するに,右上から左下に向かう斜めの成分の平均をとるという操作です。

この操作を,最初に作った軌道行列に対して行うと,元の信号が取り出されます。つまり,$x^\text{rec}_i = x_i,\ \forall i$ です。したがって,行列から元の信号を復活させる自然な操作だと思うことができます。
式で書くと,次のようになります。
$K \ge L$ のとき
$$
x^\text{rec}_i = \begin{cases}\frac{1}{j}\sum_{k=1}^{j} \widetilde{x}_{k, j-k+1} & (0\le j\le L-1) \\
\frac{1}{L}\sum_{k=1}^{L} \widetilde{x}_{k, j-k+1} & (L-1 < j< K-1) \\
\frac{1}{N-j+1}\sum_{k=k-K+1}^{N-K+1} \widetilde{x}_{k, j-k+1} & (K-1\le j\le N-1)
\end{cases}
$$
$K < L$ のとき
$$
x^\text{rec}_i = \begin{cases}\frac{1}{j}\sum_{k=1}^{j} \widetilde{x}_{j-k+1, k} & (0\le j\le K-1) \\
\frac{1}{K}\sum_{k=1}^{K} \widetilde{x}_{j-k+1, k} & (K-1 < j< L-1) \\
\frac{1}{N-j+1}\sum_{k=k-L+1}^{N-L+1} \widetilde{x}_{j-k+1, k} & (L-1\le j\le N-1)
\end{cases}
$$
特異スペクトル解析の実装方法
以上述べたことをpythonで実装してみます。以下に実装例を示します。このプログラムを適当な名前 (ssa-demo.py とします) をつけて,適当なディレクトリ (~/Desktop/labcode/python/ssa とします) に保存します。
import numpy as np
import matplotlib.pyplot as plt
from scipy import linalg
#------------------------------------------------
# --- 時系列データを生成
# 時刻のndarrayを作成
N = 1000
ts = 0.0
te = 1.0
t = np.linspace(ts, te, N)
# 周期的な成分
amp = np.exp(t) - np.exp(0.0)
freq = 10.0 + 5.0*t
oscil = amp*np.sin(2.0*np.pi*freq*t)
# トレンド
trend = 3.0*t**3
# ノイズ
noise = 0.10*np.random.randn(len(t))
# 信号 = 周期的な成分 + トレンド + ノイズ
x = oscil + trend + noise
#------------------------------------------------
# --- 特異スペクトル解析
# 軌道行列を生成
K = 600
L = N - K + 1
X = np.array([x[i:i+K] for i in range(L)])
# 時系列データを分解
U, s, Vh = linalg.svd(X)
# 重要な成分を選択
indx_rec = [1, 2, 3, 4]
# indx_rec = [0]
Sigma_tilde = np.zeros((L, K))
for i in range(min(L, K)):
if i in indx_rec:
Sigma_tilde[i, i] = s[i]
# 再構成
X_tilde = np.dot(U, np.dot(Sigma_tilde, Vh))
# diagonal averaging (右上から左下に向かう斜めの成分の平均)
x_rec = np.zeros(N)
for i in range(N):
value = 0.0 # 値を 0 にセット
count = 0 # 斜めの成分がいくつあるかのカウント
for j in range(L):
row = j # 行
col = i - j # 列
# 列が存在するかのチェック
if (col < 0):
break # 左端に到達した場合は終わり
elif (col >= K):
continue # colがKより大きい場合は何もしない(X_rec は LxK行列)
value += X_tilde[row, col] # valueに加える
count += 1 # countを1増やす
# breakで出てくる or rowがL-1に達したらloop終了。countで割る (平均)
x_rec[i] = value/float(count)
#------------------------------------------------
# --- プロット
fig, (ax01, ax02, ax03) = plt.subplots(nrows=3, figsize=(6, 8))
plt.subplots_adjust(wspace=0.0, hspace=0.6)
ax01.plot(np.log(s), 'o-', color='black', )
ax01.plot(indx_rec, np.log(s[indx_rec]), 'o', color='red')
ax01.set_xlabel('index')
ax01.set_ylabel('$\log\sigma$')
ax02.plot(t, oscil, '-', color='red', label='oscil')
ax02.plot(t, trend, '-', color='blue', label='trend')
ax02.plot(t, noise, '-', color='green', label='noise')
ax02.set_xlabel('time')
ax02.legend()
ax03.plot(t, x, '-', color='black', label='sig')
ax03.plot(t, oscil, color='red', label='oscil')
# ax03.plot(t, trend, '-', color='blue', label='trend')
ax03.plot(t, x_rec, '--', color='orange', label=f'rec by {indx_rec}', )
ax03.set_xlabel('time')
ax03.legend()
plt.show()プログラムを実行する
ターミナルを開き,
$ cd ~/Desktop/labcode/python/ssaと入力し,先程プログラムを保存したディレクトリに移動します。あとは以下のコマンドでssa-demo.pyを実行するだけです。( $マークは無視してください)
$ python3 ssa-demo.py実行結果
次のような画面が立ち上がれば成功です!
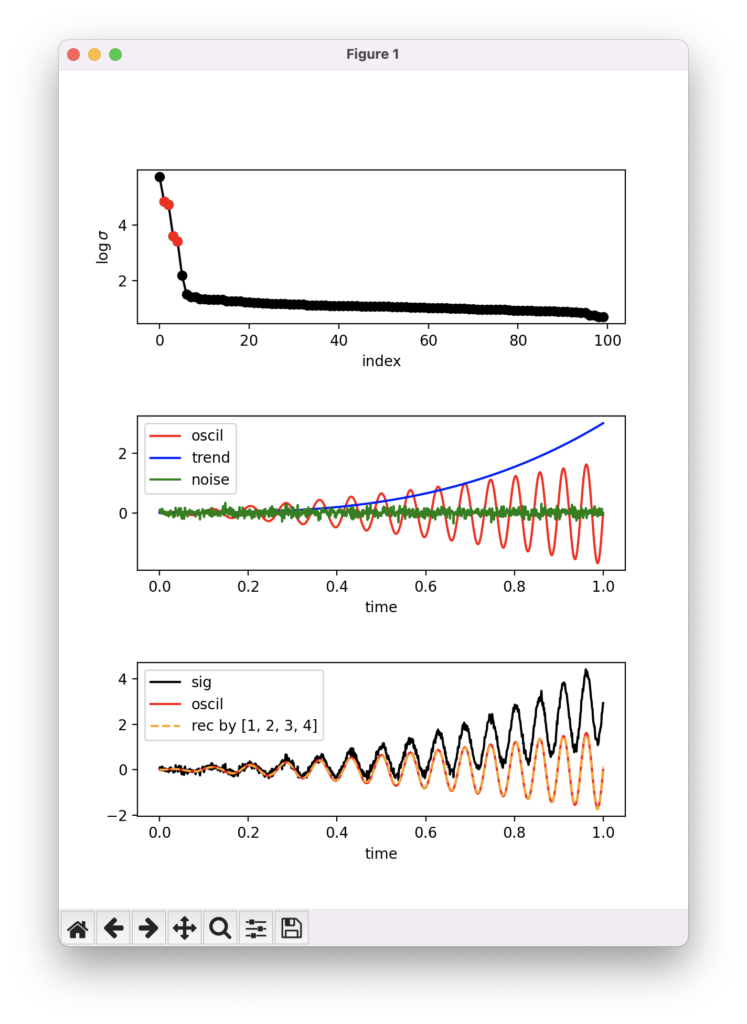
一段目は特異値の大きさを大きさの順に並べたもので,縦軸は対数表示になっています。
二段目は,入力信号に用いた振動成分,トレンド,ノイズを示しています。入力信号はこれらの成分の和になります。目標はこれらを分離することです。
三段目は,黒で入力信号,赤は振動成分で,オレンジ色の点線が,index 1, 2, 3, 4 に対応する特異値のみ (一段目の赤の特異値です)を残して再構成したもので,振動成分をよく抽出できていることがわかります。
次にトレンド成分を抽出してみましょう。38行目をコメントアウトし,39行目をアンコメントアウト
# indx_rec = [1, 2, 3, 4]
indx_rec = [0]すると,index 0 (最も大きな成分)のみで再構成することができます。
結果表示の部分も変えるために,84行目をコメントアウトし,85行目をアンコメントアウト
# ax03.plot(t, oscil, color='red', label='oscil')
ax03.plot(t, trend, '-', color='blue', label='trend')しておきましょう。結果は次のようになるはずです。
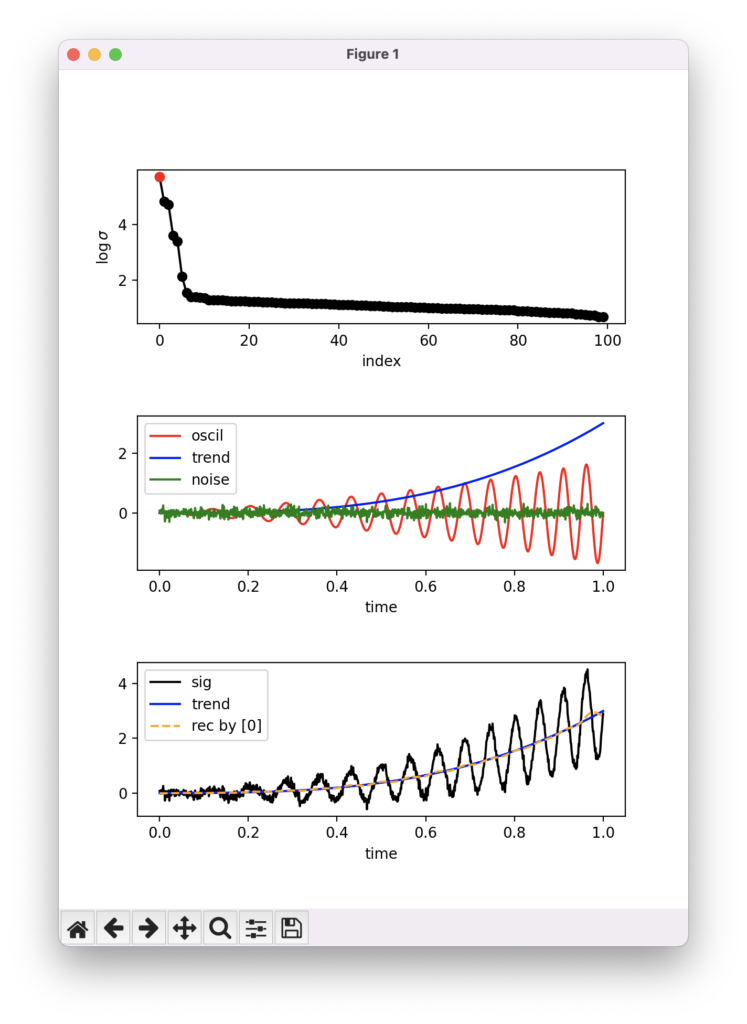
今度は,トレンド成分がよく抽出できています(右端で少しだけ歪みが見られます)。
したがって,ノイズ成分を落としたければ,index 0, 1, 2, 3, 4の成分で再構成すれば良いことになるでしょう。
コードの解説
上に示したコードの解説をします。
import numpy as np
import matplotlib.pyplot as plt
from scipy import linalgまず,必要なモジュールをインポートします。
#------------------------------------------------
# --- 時系列データを生成
# 時刻のndarrayを作成
N = 1000
ts = 0.0
te = 1.0
t = np.linspace(ts, te, N)
# 周期的な成分
amp = np.exp(t) - np.exp(0.0)
freq = 10.0 + 5.0*t
oscil = amp*np.sin(2.0*np.pi*freq*t)
# トレンド
trend = 3.0*t**3
# ノイズ
noise = 0.10*np.random.randn(len(t))
# 信号 = 周期的な成分 + トレンド + ノイズ
x = oscil + trend + noiseつぎに,テスト時系列データを作成します。テスト時系列データは周期的な成分とトレンド成分,ノイズ成分からなります。
振動成分は,振幅が指数関数的に成長し,振動数が1次関数的に増大してゆくものを仮定しました。
トレンド成分は三次関数で,ノイズはホワイトノイズを与えます。
#------------------------------------------------
# --- 特異スペクトル解析
# 軌道行列を生成
K = 100
L = N - K + 1
X = np.array([x[i:i+K] for i in range(L)])ここから,特異スペクトル解析が始まります。まず,窓の幅を決めます。
一番下の段で軌道行列を作成しています。リスト内包表記を使用していますが,index を一つずつずらして,$L\times K$ 行列を作成しているだけです。
# 軌道行列を特異値分解
U, s, Vh = linalg.svd(X)軌道行列に対して特異値分解を適用します。scipy で用意されている linalg.svd を適用します。戻り値は上で定義した,左特異行列,特異値の1次元アレイ,右特異行列です。
# 重要な成分を選択
indx_rec = [1, 2, 3, 4]
# indx_rec = [0]
Sigma_tilde = np.zeros((L, K))
for i in range(min(L, K)):
if i in indx_rec:
Sigma_tilde[i, i] = s[i]
# 再構成
X_tilde = np.dot(U, np.dot(Sigma_tilde, Vh))特異値のうち,残したい特異値のみを対角成分に持ち,重要な成分以外を0にした行列 $\widetilde{\mathsf{\Sigma}}$ を生成します。残したい成分は indx_rec というリストで選択できるようにしています。
これを用いて,最終段で np.dotを使って行列の積
$$
\widetilde{\mathsf{X}} = \mathsf{U}\widetilde{\mathsf{\Sigma}}\mathsf{V}^\top
$$
を計算し,再構成します。
# diagonal averaging (右上から左下に向かう斜めの成分の平均)
x_rec = np.zeros(N)
for i in range(N):
value = 0.0 # 値を 0 にセット
count = 0 # 斜めの成分がいくつあるかのカウント
for j in range(L):
row = j # 行
col = i - j # 列
# 列が存在するかのチェック
if (col < 0):
break # 左端に到達した場合は終わり
elif (col >= K):
continue # colがKより大きい場合は何もしない(X_rec は LxK行列)
value += X_tilde[row, col] # valueに加える
count += 1 # countを1増やす
# breakで出てくる or rowがL-1に達したらloop終了。countで割る (平均)
x_rec[i] = value/float(count)$\mathsf{X}^\text{rec}$ に diagonal averaging を適用して,時系列データに戻します。
#------------------------------------------------
# --- プロット
fig, (ax01, ax02, ax03) = plt.subplots(nrows=3, figsize=(6, 8))
plt.subplots_adjust(wspace=0.0, hspace=0.6)
ax01.plot(np.log(s), 'o-', color='black', )
ax01.plot(indx_rec, np.log(s[indx_rec]), 'o', color='red')
ax01.set_xlabel('index')
ax01.set_ylabel('$\log\sigma$')
ax02.plot(t, oscil, '-', color='red', label='oscil')
ax02.plot(t, trend, '-', color='blue', label='trend')
ax02.plot(t, noise, '-', color='green', label='noise')
ax02.set_xlabel('time')
ax02.legend()
ax03.plot(t, x, '-', color='black', label='sig')
# ax03.plot(t, oscil, color='red', label='oscil')
ax03.plot(t, trend, '-', color='blue', label='trend')
ax03.plot(t, x_rec, '--', color='orange', label=f'rec by {indx_rec}', )
ax03.set_xlabel('time')
ax03.legend()
plt.show()コードの残りの部分は,プロットをしている部分です。
最後に
今回は,特異スペクトル解析というフーリエ解析とも,ウェーブレット解析とも違った時系列データの成分分析の手法を紹介しました。テスト信号を用いたデモンストレーションで振動成分とトレンド成分,ノイズ成分が分離できることがわかったかと思います。
ぜひお手持ちのデータに適用してみてください!
参考文献
この記事を書くにあたって,以下のサイト,文献を参考にしました。数学的なことをもっと知りたい方は,文献にあたってみてください。
- https://ni4muraano.hatenablog.com/entry/2017/02/04/230543
- N. Golyandina and A. Zhigljavsky, “Singular Spectrum Analysis for Time Series”, Springer (2013).




