pythonで周波数解析したいと思ったことはありませんか。
離散フーリエ変換を使用して，手持ちのデータに特定の周波数成分がどれくらい含まれているかを可視化してみましょう。
周波数解析ができるようになると，データの解析の幅が広がります。 例えば，音声データの定量的な解析ができるようになったり，時系列データに含まれる特定の周期(周波数)を持つ信号を取り出し，ゆっくりと変化するトレンド成分や急激に振動するノイズ成分の除去を行うことができます。
macOS Big Sur, python3.7.9
Pythonで学ぶ偏微分方程式の数値シミュレーションの技術書を販売中
計算方法、グラフやアニメーションの作成方法、計算ログの残し方を惜しみなく解説しています！
理論と実装の溝を埋めてくれる良書です！
周波数解析
周波数解析には，離散フーリエ変換 (DFT; discrete Fourier transform) がよく用いられます。DFT は入力デジタル信号に含まれる周波数成分を取り出すことができます。
長さ $T$秒，データ長 $N$ のデジタル信号 $x_i\ (i=1, \dots, N)$ に対して，DFTは
$$
X_k = \sum_{i=0}^{N-1} x_i \exp\left(-2\pi\sqrt{-1} \frac{ik}{N}\right)
$$
と定義されます (元信号の添字として $i$ を使用してしまったので，虚数単位を $\sqrt{-1}$ と表します)。$X_k$ は複素数です。
$k$ は周波数 (振動数) に対応する添字で，周波数 $k/T$ に対応します。
$|X_k|/N$ を振幅スペクトルといい，元信号に含まれる周波数 $k/T$ の振動の振幅の強さを表します。
DFT の実行方法
ソースコード
DFT を行うにはnumpyライブラリのfftモジュールを使うと簡単に実現できます。
以下のようなコードを書きます。
import numpy as np
import matplotlib.pyplot as plt
# テストデータの生成
N = 1000
ts = 0.0
te = 1.0
t = np.linspace(ts, te, N)
x = 1.0*np.sin(2.0*np.pi*100.0*t) + 0.5*np.cos(2.0*np.pi*10.0*t) + 0.05*np.random.randn(N)
# DFT
X = np.fft.fft(x)
dt = t[1] - t[0] # 時間刻み
f = np.fft.fftfreq(N, dt) # Xのindexに対応する周波数のndarrayを取得
# データをプロット
fig, (ax01, ax02) = plt.subplots(nrows=2, figsize=(6, 8))
plt.subplots_adjust(wspace=0.0, hspace=0.6)
ax01.set_xlabel('time (s)')
ax01.set_ylabel('x')
ax01.plot(t, x) # 入力信号
# ax02.set_xlim(0, f.max())
ax02.set_xlabel('frequency (Hz)')
ax02.set_ylabel('|X|/N')
ax02.plot(f, np.abs(X)/N) # 振幅スペクトル
plt.show()上で記述したコードをfft-demo.pyという名前でDesktop/LabCode/python/frequency-analysisディレクトリに保存します。
プログラムを実行する
ターミナルを開き，
$ cd Desktop/LabCode/python/frequency-analysisと入力し，ディレクトリを移動します。あとは以下のコマンドでfft-demo.pyを実行するだけです。（$マークは無視してください）
$ python fft-demo.py実行結果
実行すると以下のようなウィンドウが立ち上がるはずです。
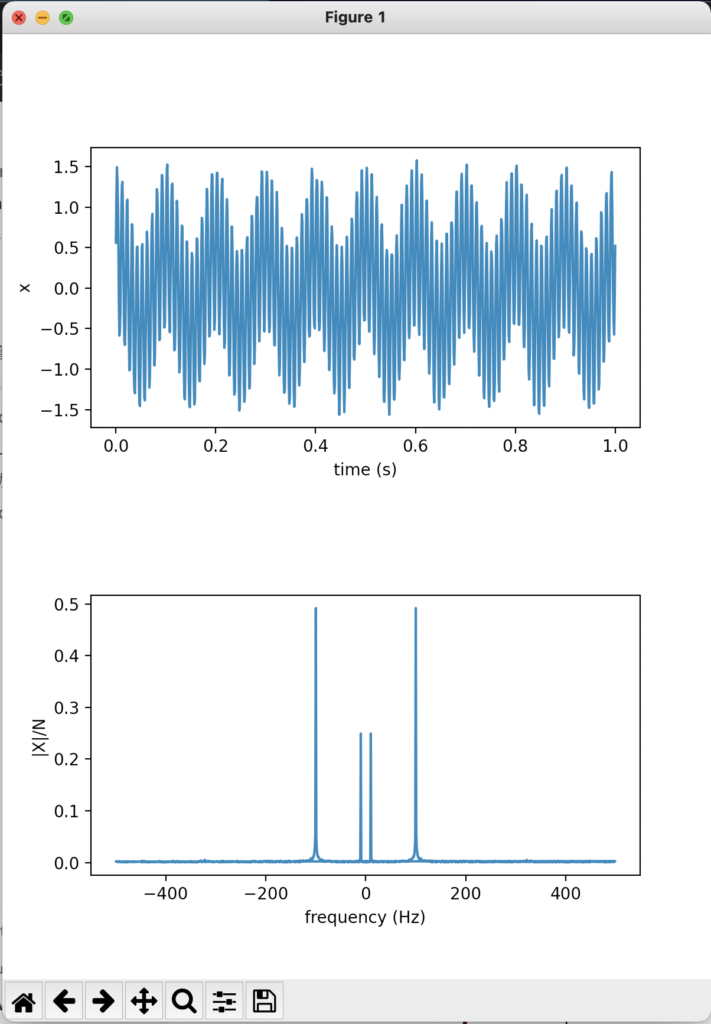
- 一段目は入力信号を表しています。
- 二段目は振幅スペクトルを表していて，入力信号に含まれる100 Hzと10 Hzにピークが見られます！
- 振幅スペクトルの大きさは100 Hzが0.5，10 Hzが0.25となっていて，入力信号の振幅の大きさの比と対応しています。
- 入力信号が実数の場合，基本的には正の周波数部分に着目し，振幅スペクトルを二倍した値の振動が含まれると解釈すれば十分です! (つまり，上の例だと，50 Hzの振幅スペクトルが0.25なので，振幅 0.5 で周波数 50 Hz の振動成分が含まれると解釈する)。
- 振幅が仮定した信号の1/2となっている理由や，負の周波数部分については今後の記事で詳しく述べます。
コードの解説
上で書いたソースコードの解説をしていきます。
import numpy as np
import matplotlib.pyplot as pltまず，numpyとmatplotlibをimportします。
# テストデータの生成
N = 1000
ts = 0.0
te = 1.0
t = np.linspace(ts, te, N)
x = 1.0*np.sin(2.0*np.pi*100.0*t) + 0.5*np.cos(2.0*np.pi*10.0*t) + 0.05*np.random.randn(N)こちらでは，テストデータを生成します。
ここでは，振幅1.0で周波数100kHzのsin関数と振幅0.5で周波数10 Hzのcos関数，振幅0.05のホワイトノイズの和で表される1.0秒間の信号を作っています。サンプリングは1.0秒間で1000点なので，1000Hzです。
# DFT
X = np.fft.fft(x)
dt = t[1] - t[0] # 時間刻み
f = np.fft.fftfreq(N, dt) # Xのindexに対応する周波数のndarrayを取得DFTをnp.fft.fftで行い，X に格納します。
また，X のindexに対応する周波数のndarrayを np.fft.fftfreqで取得し，fに格納します。
# データをプロット
fig, (ax01, ax02) = plt.subplots(nrows=2, figsize=(6, 8))
plt.subplots_adjust(wspace=0.0, hspace=0.6)
ax01.set_xlabel('time (s)')
ax01.set_ylabel('x')
ax01.plot(t, x) # 入力信号
# ax02.set_xlim(0, f.max())
ax02.set_xlabel('frequency (Hz)')
ax02.set_ylabel('|X|/N')
ax02.plot(f, np.abs(X)/N) # 振幅スペクトル
plt.show()さいごに， $|X|$ を $N$ で割って振幅スペクトルにし，解析結果をプロットします。
興味があるのは正の周波数部分なので，ax02.set_xlim(0, f.max())の部分をアンコメントしても良いでしょう。
