はじめに
エマグラムを眺めると大気の安定度がわかることは、以前の記事で紹介しました。
一方、気温や湿度の鉛直分布から求められる定量的な指数が提案されており、この指数を用いて大気の安定度や雷雨の可能性等を見積もることができます。
今回は、これらの指数の内容と、MetPyを使った計算方法について紹介します。
macOS Monterey 12.6.2, Python 3.9.15, MetPy 1.3.1
Pythonでやってみる気象データ解析の技術書を販売中
¥2,500 → ¥1,500 今なら40%OFF!!
気象の勉強をされている方必読!
気象予報士でもある著者がわかりやすく解説
プログラムを公開しているのでお手元で試せます!
大気の鉛直プロファイルから計算できる指標
LCL (Lifted Condensation Level: 持ち上げ凝結高度)
地上付近の空気塊を持ち上げたとき、凝結が起こる高度です。エマグラムでは、地上付近の気温を通る乾燥断熱線と露点温度を通る等飽和混合比線が交わる点です。
MetPyでは、 metpy.calc.lcl(pressure, temperature, dewpoint, max_iters=50, eps=1e-05)で計算することができます。
LFC (Level of Free Convection: 自由対流高度)
地上付近の空気塊を持ち上げたときにその空気塊の温度が、周囲の気温 (状態曲線で表される気温) よりも高くなった高度のことです。
LFCよりも上では、空気塊は浮力を得て、強制上昇がなくても上昇することができます。LFCが小さいほど対流活動が起こりやすいと解釈することもできます。
MetPyでは、高層気象観測のデータから metpy.calc.lfc(pressure, temperature, dewpoint, parcel_temperature_profile=None, dewpoint_start=None, which='top')で計算することができます。
EL (Equilibrium Level: 平衡高度)
地上付近の空気塊を断熱的に持ち上げたとき、自由対流高度よりも上で浮力が0になる高度です。複数の高度の候補がある場合がありますが、最も高い高度または (後で出てくる) CAPEを最大にする高度として一つ選択します。この高度は対流雲の背の高さの目安となります。
MetPyでは、高層気象観測のデータから metpy.calc.el(pressure, temperature, dewpoint, parcel_temperature_profile=None, which='top')で計算することができます。
CIN (Convective Inhibition: 対流抑制)
対流 (convective) 抑制 (inhibition) で下の図の面積で表される量です。地表付近の空気塊を自由対流高度まで上昇させるために必要なエネルギーを表します。次のように定義されます。
$$ \text{CIN} = -g\int_{z_0}^{\text{LFC}}\frac{T(z) – \overline{T(z)}}{\overline{T(z)}}\mathrm{d}z $$
ここで 、 $T(z)$ は空気塊の温度で飽和するまでは乾燥断熱減率に沿って変化させ、飽和してからは湿潤断熱減率に沿って変化させます。$\overline{T(z)}$ は状態曲線で表される「周囲の」空気の温度です。
静水圧平衡 $\mathrm{d}p = -\rho g\mathrm{d}z$ と状態方程式 $p = \rho R T$ を用いると、
$$ \mathrm{d}(\ln p) = \frac{\mathrm{d}p}{p} = -\frac{g\mathrm{d}z}{RT} $$
なので、上の式は
$$ \text{CIN} = R\int_{p_0}^{\text{LFC}} (T(p) – \overline{T(p)})\mathrm{d}(\ln p) $$
と書けます。これで、気圧-温度のデータから計算することができます。
CINが小さいほど、対流が発生しやすいと言えます。
CAPE (Convective Available Potential Energy: 対流有効位置エネルギー)
対流 (convective) 有効 (available) 位置エネルギー (potential energy) で、下の図の面積で表される量です。自由対流高度よりも上では空気塊は浮力を受けてエネルギーを得ることができます。このエネルギーの大きさを表し、次のように定義されます。
$$ \text{CAPE} = g \int_{\text{LFC}}^{\text{EL}}\frac{T(z) – \overline{T(z)}}{\overline{T(z)}}\mathrm{d}z $$
CINでやったのと同じ変形をすることで、
$$ \text{CAPE} = -R \int_{\text{LFC}}^{\text{EL}}(T(p) – \overline{T(p)})\mathrm{d}(\ln p) $$
と書けます。
この値が大きいと、大気の状態が不安定であると言えます。不安定度の一つの目安として 「シビア現象の監視・予測について」(2021年3月) には、次のように説明されています。
| CAPE (J/kg) | 大気の安定性 |
|---|---|
| 0以下 | 安定 |
| 0から1000 | やや不安定 |
| 1000から2500 | 中程度に不安定 |
| 2500から3500 | 非常に不安定 |
| 3500以上 | 極端に不安定 |
MetPyではCINとCAPEは、高層気象観測のデータからmetpy.calc.surface_based_cape_cin(pressure, temperature, dewpoint)で計算できます。(注:MetPyで計算されるCINは符号が逆です。)
SSI (Shawalter Stability Index: ショワルター安定指数)
SSIは500 hPaの温度 $T_{500}$ から、850 hPaにある空気塊を500 hPaまで上昇させたときの温度 $T_{850\to 500}$ を差し引いた値です。
空気塊の上昇のさせ方のルールは同じで、飽和するまでは乾燥断熱線に沿って、飽和してからは湿潤断熱線に沿って上昇させます。
$$ \text{SSI} = T_{500} – T_{850\to 500} $$
SSIが負の値なら850 hPaの空気塊を持ち上げたときに500 hPaの気温よりも高いことを意味するため、大気の状態が不安定です。 「シビア現象の監視・予測について」(2021年3月) には、次のように説明されています。
| SSI (℃) | 大気の安定性 |
|---|---|
| 0より大きい | 安定 |
| 0から-3 | やや不安定 (雷雨の可能性あり) |
| -3から-6 | 中程度に不安定 (激しい雷雨の可能性あり) |
| -6から-9 | 非常に不安定 |
| -9より小さい | 極度に不安定 |
MetPyでは、、高層気象観測のデータからmetpy.calc.showalter_index(pressure, temperature, dewpoint) で計算できます。
KI (K-index: K指数)
KI は次のように定義されます。
$$ K\text{-index} = (T_{850} – T_{500}) + T_\text{d, 850} – (T_{700} – T_\text{d, 700}) $$
ここで、$T_{\text{d, 850}}$ 、$T_{\text{d, 700}}$ は850 hPaおよび700 hPaの露点温度です。
値が大きいほど大気の状態は不安定で、雷雨の可能性の目安となります。 「シビア現象の監視・予測について」(2021年3月) には、次のように説明されています (最後は40より大きいとするべき?ただし、あくまで目安なので、こだわらなくて良いはずです)。
| KI (℃) | 雷雨の可能性 |
|---|---|
| 15以下 | なし |
| 15から20 | 20% |
| 21から25 | 20から40% |
| 26から30 | 40から60% |
| 31から35 | 60から80% |
| 36から40 | 80から90% |
| 40以上 | ほぼ100% |
MetPyでは、高層気象観測のデータから metpy.calc.k_index(pressure, temperature, dewpoint, vertical_dim=0) で計算できます。
実装例
まずは、高層気象観測のデータを用意します。
気圧、温度、湿度が含まれたデータセットを用意しました。ダウンロードしてお使いください。なお、以前のものよりも解像度が高いです。一行目に気圧、二行目に気温、三行目に相対湿度が含まれています。
上で述べた指標を計算して、エマグラムの上に表示しておきましょう。実装例を以下に示します。以下のコードをコピーしてplot-emagram-and-calc-params.pyという名前で,適当なディレクトリ(ここでは,~/Desktop/labcode/python/plot-emagram-and-calc-params とします)に保存します。上に示したデータファイルも同じディレクトリに入れておきましょう。
import matplotlib.pyplot as plt
import metpy.calc as mpcalc
from metpy.plots import SkewT
from metpy.units import units
import numpy as np
#------------------------------------------------------------------------------
# データを読み込む
fname = "20170705_09JST_47807.txt"
data = np.genfromtxt(fname=fname, unpack=True)
prss_pcl = 950 * units.hPa # 持ち上げる空気塊がある気圧
prss = data[0]*units.hPa # 気圧
tmpr = data[1]*units.degC # 気温
rhmd = data[2] # 相対湿度
#------------------------------------------------------------------------------
# --- 計算
# 気温と相対湿度から露点温度を計算する。
dewp = mpcalc.dewpoint_from_relative_humidity(tmpr, rhmd/100.0)
# 持ち上げる空気塊の気圧のインデックスを取得
i_prss_pcl = np.argmin(np.abs(prss_pcl.magnitude - prss.magnitude))
# 空気塊を持ち上げた場合の温度変化を計算する
prss_wlcl, tmpr_wlcl, dewp_wlcl, prof_wlcl = mpcalc.parcel_profile_with_lcl(prss[i_prss_pcl:], tmpr[i_prss_pcl:], dewp[i_prss_pcl:])
# LCL (Lifted Condensation Level: 持ち上げ凝結高度)
lcl_prss, lcl_tmpr = mpcalc.lcl(prss[i_prss_pcl], tmpr[i_prss_pcl], dewp[i_prss_pcl])
# LFC (Level of Free Convection: 自由対流高度) を計算する
lfc_prss, lfc_tmpr = mpcalc.lfc(prss[i_prss_pcl:], tmpr[i_prss_pcl:], dewp[i_prss_pcl:])
# EL (Equilibrium Level: 平衡高度) を計算する
el_prss, el_tmpr = mpcalc.el(prss, tmpr, dewp)
# CAPE (convective available potential energy: 対流有効位置エネルギー) と
# CIN (convective inhibition: 対流抑制) を計算する
cape, cin = mpcalc.surface_based_cape_cin(prss, tmpr, dewp)
# SSI (Shawalter Stability Index: ショワルター安定指数) を計算する
ssi = mpcalc.showalter_index(prss, tmpr, dewp)
# KI (K-index: K指数) を計算する
ki = mpcalc.k_index(prss, tmpr, dewp)
#------------------------------------------------------------------------------
# *** プロット
# --- プロット範囲の設定
xmax = 40 # 横軸(温度)の最大値
xmin = -90 # 横軸(温度)の最小値
ymin = 100 # 縦軸(気圧)の最小値
ymax = 1020 # 縦軸(気圧)の最大値
# --- 全般の設定
fig = plt.figure(figsize=(210/25.4, 294/25.4), dpi=100)
out_fig_path = 'emagram.png'
# --- 安定度の指数を書く。値に応じて安定度のコメント、色を変える
fig.text(0.05, 0.95, f"starting parcel pressure = {prss[i_prss_pcl].magnitude:.0f} hPa")
fig.text(0.05, 0.93, f"LCL = {lcl_prss.magnitude:.0f} hPa")
fig.text(0.05, 0.91, f"LFC = {lfc_prss.magnitude:.0f} hPa")
fig.text(0.05, 0.89, f"EL = {el_prss.magnitude:.0f} hPa")
fig.text(0.55, 0.95, f"CIN = {cin.magnitude:.0f} J/kg")
fig.text(0.55, 0.93, f"CAPE = {cape.magnitude:.0f} J/kg")
fig.text(0.55, 0.91, f"SSI = {ssi[0].magnitude:.0f}℃")
fig.text(0.55, 0.89, f"KI = {int(ki.magnitude):.0f}℃")
# --- 図の設定
skew = SkewT(fig, rotation=0, aspect=150)
# --- 軸の設定
skew.ax.set_xlim(xmin, xmax)
skew.ax.set_ylim(ymax, ymin)
# --- ラベルの設定
skew.ax.set_xlabel('Temperature (℃)')
skew.ax.set_ylabel('Pressure (hPa)')
# --- 気温,露点温度,風の鉛直分布をプロットする
skew.plot(prss, tmpr, 'red')
skew.plot(prss, dewp, 'blue')
skew.plot(prss_wlcl, prof_wlcl, 'black')
# --- LCL、LFCおよびELをプロット
skew.plot(lcl_prss, lcl_tmpr, 'ko', markerfacecolor='black')
skew.plot(lfc_prss, lfc_tmpr, 'ko', markerfacecolor='black')
# --- 乾燥断熱線のプロット
t0 = np.arange(200, 360, 10)*units.K # プロットする乾燥断熱線のスタート温度
# 乾燥断熱線をプロット
skew.plot_dry_adiabats(t0=t0, lw=0.5, colors='red')
# ラベルを350hPaに付す
for t in t0:
p1 = 350*units.hPa
t1 = mpcalc.dry_lapse(p1, t, 1000*units.hPa) # p1=350hPaまで乾燥断熱線に従って持ち上げたときの温度
if t1 < xmin*units.degC:
continue
skew.ax.text(t1, p1, f'{t.magnitude}', fontsize=9,
horizontalalignment='center', color='red')
# --- 湿潤断熱線のプロット
t0 = np.arange(245, 320, 5)*units.K # プロットする湿潤断熱線のスタート温度
# 湿潤断熱線のプロット
skew.plot_moist_adiabats(t0=t0, lw=0.5, colors='green')
# ラベルを250hPaに付す
for t in t0:
p1 = 250 * units.hPa
t1 = mpcalc.moist_lapse(p1, t, 1000*units.hPa) # p1=250hPaまで湿潤断熱線に従って持ち上げたときの温度
if t1 < xmin*units.degC:
continue
skew.ax.text(t1, p1, f'{t.magnitude}', fontsize=9,
horizontalalignment='center', color='green')
# --- 等飽和混合比線のプロット
# プロットする混合比の値,プロットする気圧の範囲を指定する
mixing_ratio = np.array([0.2, 0.4, 0.6, 1, 2, 4, 5, 10, 15, 20, 25, 30, 35]).reshape(-1, 1) * units('g/kg')
pressure = np.arange(1000, 10, -50)*units.hPa
# 等飽和混合比線のプロット
skew.plot_mixing_lines(mixing_ratio=mixing_ratio, pressure=pressure, lw=0.5, colors='blue')
# ラベルを110hPa付近に付す
for i, mr in enumerate(mixing_ratio.flatten()):
p1 = 110 * units.hPa + i%2 * 10 * units.hPa
dewpt = mpcalc.dewpoint(mpcalc.vapor_pressure(p1, mr))
if mr.magnitude < 1.0:
skew.ax.text(dewpt, p1, f'{mr.magnitude:.1f}', fontsize=9,
horizontalalignment='center', color="blue")
else:
skew.ax.text(dewpt, p1, f'{mr.magnitude:.0f}', fontsize=9,
horizontalalignment='center', color="blue")
# CINとCAPEに相当する部分をそれぞれ青と赤で塗りつぶす
skew.shade_cin(prss_wlcl, tmpr_wlcl, prof_wlcl)
skew.shade_cape(prss_wlcl, tmpr_wlcl, prof_wlcl)
#------------------------------------------------------------------------------
# --- 図の保存
plt.savefig(out_fig_path, transparent=False)
プログラムを実行する
ターミナルを開き、
$ cd ~/Desktop/labcode/python/plot-emagram-and-calc-params
と入力し、ディレクトリを移動します。あとは以下のコマンドを実行するだけです。( $マークは無視してください)
$ python plot-emagram-and-calc-params.py
実行結果
~/Desktop/labcode/python/plot-emagram-and-calc-params にemagram.pngというファイルができて、以下のようになっていれば成功です!
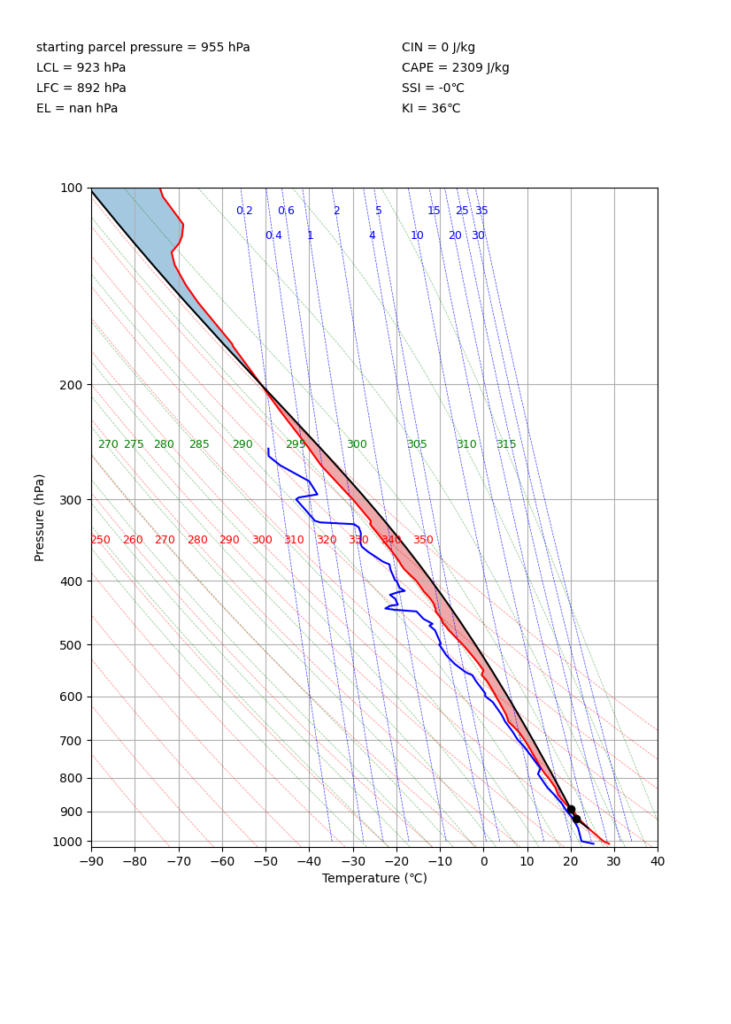
赤実線で気温のプロファイル、青実線で露点温度のプロファイルが描画されています。
955 hPa付近から黒線がプロットされていて、これは955 hPaの空気塊を断熱的に持ち上げたときの温度プロファイルになります (気象予報士試験ではこれを作図する問題が出題されることもあります)。
920 hPa付近に黒の点があって折れ曲がり、890 hPa付近にも黒の点があり赤実線と交わっています。これらはそれぞれ LCL と LFC です。図の上部左側にはこれらの値を出力しています。
さらに上空で、再び黒実線と赤実線が交わっています。ここがELと見積もることができます (約200 hPa)。ただし、MetPyの関数では露点温度プロファイルがないと計算してくれないようです (nan hPa となっています)。
図の上部右側には上で説明した大気安定度の指標の値を出力しています。値だけ見ると大気の安定度は悪い事がわかります。ちなみに、例として使った2017年7月5日は平成29年7月九州北部豪雨があった日です。
コードの解説
上に書いたソースコードの解説をしていきます。ほとんどが以前の記事と同じです。特に異なる部分を中心に解説します。
import matplotlib.pyplot as plt
import metpy.calc as mpcalc
from metpy.plots import SkewT
from metpy.units import units
import numpy as np
#------------------------------------------------------------------------------
# データを読み込む
fname = "20170705_09JST_47807.txt"
data = np.genfromtxt(fname=fname, unpack=True)
prss_pcl = 950 * units.hPa # 持ち上げる空気塊がある気圧
prss = data[0]*units.hPa # 気圧
tmpr = data[1]*units.degC # 気温
rhmd = data[2] # 相対湿度
この部分は必要なモジュールを読み込み、データファイルを定義してデータの読み込みを行っています。
prss_pcl はスタートさせる空気塊のある気圧面の値です。ここでは、950 hPaとしています。地上のものを使いたい場合は、非常に大きな値 (例えば、10000 hPa等 )を指定すればよいでしょう。(ただし、あとで分かるように、今回の実装では、prss_pcl で指定した気圧面のものと最も近いものとなるため、厳密に指定した気圧面のものになるとは限りません。)
#------------------------------------------------------------------------------
# --- 計算
# 気温と相対湿度から露点温度を計算する。
dewp = mpcalc.dewpoint_from_relative_humidity(tmpr, rhmd/100.0)
# 持ち上げる空気塊の気圧のインデックスを取得
i_prss_pcl = np.argmin(np.abs(prss_pcl.magnitude - prss.magnitude))
# 空気塊を持ち上げた場合の温度変化を計算する
prss_wlcl, tmpr_wlcl, dewp_wlcl, prof_wlcl = mpcalc.parcel_profile_with_lcl(prss[i_prss_pcl:], tmpr[i_prss_pcl:], dewp[i_prss_pcl:])
# LCL (Lifted Condensation Level: 持ち上げ凝結高度)
lcl_prss, lcl_tmpr = mpcalc.lcl(prss[i_prss_pcl], tmpr[i_prss_pcl], dewp[i_prss_pcl])
# LFC (Level of Free Convection: 自由対流高度) を計算する
lfc_prss, lfc_tmpr = mpcalc.lfc(prss[i_prss_pcl:], tmpr[i_prss_pcl:], dewp[i_prss_pcl:])
# EL (Equilibrium Level: 平衡高度) を計算する
el_prss, el_tmpr = mpcalc.el(prss, tmpr, dewp)
# CAPE (convective available potential energy: 対流有効位置エネルギー) と
# CIN (convective inhibition: 対流抑制) を計算する
cape, cin = mpcalc.surface_based_cape_cin(prss, tmpr, dewp)
# SSI (Shawalter Stability Index: ショワルター安定指数) を計算する
ssi = mpcalc.showalter_index(prss, tmpr, dewp)
# KI (K-index: K指数) を計算する
ki = mpcalc.k_index(prss, tmpr, dewp)
読み込んだデータを使って計算を行います。
まず、気温と相対湿度から露点温度を計算します。
次に、読み込んだ気圧データ prss のうち、prss_pcl で指定した気圧と近いもののインデックスをさがします。このインデックスを i_prss_pcl とします。
空気塊を持ち上げたときの温度変化プロファイルを計算します。metpy.calc.parcel_profile_with_lcl(*pressure*, *temperature*, *dewpoint*) を使っています。MetPyのReferenceに詳しいですが、LCLにおける値を内挿して出力してくれるため、metpy.calc.parcel_profile(*pressure*, *temperature*, *dewpoint*) ではなく、こちらを使用します。
あとは、コード内のコメントにあるように、LCL、LFC、EL、CIN、CAPE、SSI、KIを次々と計算しています。
#------------------------------------------------------------------------------
# *** プロット
# --- プロット範囲の設定
xmax = 40 # 横軸(温度)の最大値
xmin = -90 # 横軸(温度)の最小値
ymin = 100 # 縦軸(気圧)の最小値
ymax = 1020 # 縦軸(気圧)の最大値
# --- 全般の設定
fig = plt.figure(figsize=(210/25.4, 294/25.4), dpi=100)
out_fig_path = 'emagram.png'
# --- 安定度の指数を書く。値に応じて安定度のコメント、色を変える
fig.text(0.05, 0.95, f"starting parcel pressure = {prss[i_prss_pcl].magnitude:.0f} hPa")
fig.text(0.05, 0.93, f"LCL = {lcl_prss.magnitude:.0f} hPa")
fig.text(0.05, 0.91, f"LFC = {lfc_prss.magnitude:.0f} hPa")
fig.text(0.05, 0.89, f"EL = {el_prss.magnitude:.0f} hPa")
fig.text(0.55, 0.95, f"CIN = {cin.magnitude:.0f} J/kg")
fig.text(0.55, 0.93, f"CAPE = {cape.magnitude:.0f} J/kg")
fig.text(0.55, 0.91, f"SSI = {ssi[0].magnitude:.0f}℃")
fig.text(0.55, 0.89, f"KI = {int(ki.magnitude):.0f}℃")
# --- 図の設定
skew = SkewT(fig, rotation=0, aspect=150)
# --- 軸の設定
skew.ax.set_xlim(xmin, xmax)
skew.ax.set_ylim(ymax, ymin)
# --- ラベルの設定
skew.ax.set_xlabel('Temperature (℃)')
skew.ax.set_ylabel('Pressure (hPa)')
# --- 気温,露点温度,風の鉛直分布をプロットする
skew.plot(prss, tmpr, 'red')
skew.plot(prss, dewp, 'blue')
skew.plot(prss_wlcl, prof_wlcl, 'black')
# --- LCL、LFCおよびELをプロット
skew.plot(lcl_prss, lcl_tmpr, 'ko', markerfacecolor='black')
skew.plot(lfc_prss, lfc_tmpr, 'ko', markerfacecolor='black')
# --- 乾燥断熱線のプロット
t0 = np.arange(200, 360, 10)*units.K # プロットする乾燥断熱線のスタート温度
# 乾燥断熱線をプロット
skew.plot_dry_adiabats(t0=t0, lw=0.5, colors='red')
# ラベルを350hPaに付す
for t in t0:
p1 = 350*units.hPa
t1 = mpcalc.dry_lapse(p1, t, 1000*units.hPa) # p1=350hPaまで乾燥断熱線に従って持ち上げたときの温度
if t1 < xmin*units.degC:
continue
skew.ax.text(t1, p1, f'{t.magnitude}', fontsize=9,
horizontalalignment='center', color='red')
# --- 湿潤断熱線のプロット
t0 = np.arange(245, 320, 5)*units.K # プロットする湿潤断熱線のスタート温度
# 湿潤断熱線のプロット
skew.plot_moist_adiabats(t0=t0, lw=0.5, colors='green')
# ラベルを250hPaに付す
for t in t0:
p1 = 250 * units.hPa
t1 = mpcalc.moist_lapse(p1, t, 1000*units.hPa) # p1=250hPaまで湿潤断熱線に従って持ち上げたときの温度
if t1 < xmin*units.degC:
continue
skew.ax.text(t1, p1, f'{t.magnitude}', fontsize=9,
horizontalalignment='center', color='green')
# --- 等飽和混合比線のプロット
# プロットする混合比の値,プロットする気圧の範囲を指定する
mixing_ratio = np.array([0.2, 0.4, 0.6, 1, 2, 4, 5, 10, 15, 20, 25, 30, 35]).reshape(-1, 1) * units('g/kg')
pressure = np.arange(1000, 10, -50)*units.hPa
# 等飽和混合比線のプロット
skew.plot_mixing_lines(mixing_ratio=mixing_ratio, pressure=pressure, lw=0.5, colors='blue')
# ラベルを110hPa付近に付す
for i, mr in enumerate(mixing_ratio.flatten()):
p1 = 110 * units.hPa + i%2 * 10 * units.hPa
dewpt = mpcalc.dewpoint(mpcalc.vapor_pressure(p1, mr))
if mr.magnitude < 1.0:
skew.ax.text(dewpt, p1, f'{mr.magnitude:.1f}', fontsize=9,
horizontalalignment='center', color="blue")
else:
skew.ax.text(dewpt, p1, f'{mr.magnitude:.0f}', fontsize=9,
horizontalalignment='center', color="blue")
# CINとCAPEに相当する部分をそれぞれ青と赤で塗りつぶす
skew.shade_cin(prss_wlcl, tmpr_wlcl, prof_wlcl)
skew.shade_cape(prss_wlcl, tmpr_wlcl, prof_wlcl)
#------------------------------------------------------------------------------
# --- 図の保存
plt.savefig(out_fig_path, transparent=False)
この部分はプロットの部分です。基本的には以前の記事のものをベースにしています。
大きな違いとしては、fig.text(0.05, 0.95, f"starting parcel pressure = {prss[i_prss_pcl].magnitude:.0f} hPa") 等で図の上部に計算した値を出力する部分、skew.plot(prss_wlcl, prof_wlcl, 'black') で空気塊を持ち上げたときのプロファイルをプロットする部分、skew.plot(lcl_prss, lcl_tmpr, 'ko', markerfacecolor='black') 等でLCLやLFCを黒点でプロットしている部分、skew.shade_cin(prss_wlcl, tmpr_wlcl, prof_wlcl) 等で、CINやCAPEに対応する部分を塗りつぶしている部分、です。
最後に
今回は、鉛直プロファイルから計算できる大気の安定度の指標について紹介しました。大雨時や竜巻等の激しい突風が発生したときと、安定した大気の状態のときのプロファイルを比べてみるのも面白いかと思います。
参考文献
本記事を執筆するに当たり、以下の文献、資料を参考にしました。
- 加藤輝之,「気象学ライブラリー3 集中豪雨と線状降水帯」,朝倉書店
- https://www.data.jma.go.jp/obd/stats/data/bosai/tornado/indices.pdf
- https://www.jma.go.jp/jma/kishou/know/expert/pdf/r2_text/r2_storm.pdf
Pythonでやってみる気象データ解析の技術書を販売中
¥2,500 → ¥1,500 今なら40%OFF!!
気象の勉強をされている方必読!
気象予報士でもある著者がわかりやすく解説
プログラムを公開しているのでお手元で試せます!




