これまでは,水平方向の大気の構造を可視化する手法について紹介してきました。大気の構造は,三次元的に把握することが大事です。もう一つの軸 (鉛直) 方向のプロットをしてみましょう。
鉛直方向の大気の構造を知る術として,エマグラムという図がよく使われます。MetPyを使ってエマグラムを描画してみます。
macOS Monterey 12.6.2, Python 3.9.15, MetPy 1.3.1
Pythonでやってみる気象データ解析の技術書を販売中
¥2,500 → ¥1,500 今なら40%OFF!!
気象の勉強をされている方必読!
気象予報士でもある著者がわかりやすく解説
プログラムを公開しているのでお手元で試せます!
エマグラムとは
エマグラム (emagram) とは,横軸に温度,縦軸に気圧を対数目盛で気圧が高い方を下にとったグラフ上に,ある地点における気温と露点の鉛直方向分布をプロットしたものです。
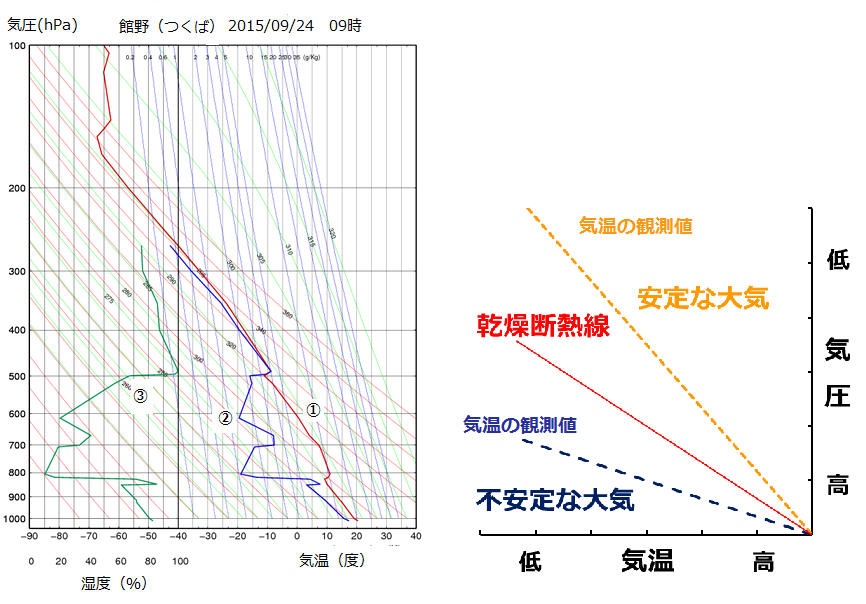
同時に湿潤断熱線,乾燥断熱線 (空気塊が飽和している時,および,していない時に持ち上げると温度がどれだけ下がっていくかを示す線です。中学校でフェーンの計算をした時に似たようなことをした記憶がある方もいらっしゃるかと思います) ,等飽和混合比線もプロットしてあるのが普通です。
エマグラムを参照することにより,ある地点における大気の鉛直構造を把握することができ,大気の安定度などを知ることができます。
大気の鉛直分布データの取得
大気の鉛直分布データは気象庁のウェブサイトで手に入ります。ゾンデという気球を打ち上げて観測しています。詳しくは,気象庁の解説「ラジオゾンデによる高層気象観測」を御覧ください。
記事執筆時 (2023/03/20) 高層気象観測を行っている地点と,地点番号 (データを取得する際に用います) は以下のとおりです (「ラジオゾンデによる高層気象観測」より)。
| 地点番号 | 地点名 | 所在地 | 緯度(度分) | 経度(度分) |
|---|---|---|---|---|
| 47401 | 稚内(わっかない) | 北海道稚内市 | 45°24.9′ | 141°40.7′ |
| 47412 | 札幌(さっぽろ) | 北海道札幌市 | 43°03.6′ | 141°19.7′ |
| 47418 | 釧路(くしろ) | 北海道釧路市 | 42°57.2′ | 144°26.3′ |
| 47582 | 秋田(あきた) | 秋田県秋田市 | 39°43.1′ | 140°06.0′ |
| 47600 | 輪島(わじま) | 石川県輪島市 | 37°23.5′ | 136°53.7′ |
| 47646 | 館野(たての) | 茨城県つくば市 | 36°03.5′ | 140°07.5′ |
| 47678 | 八丈島(はちじょうじま) | 東京都八丈島八丈町 | 33°07.3′ | 139°46.7′ |
| 47741 | 松江(まつえ) | 島根県松江市 | 35°27.5′ | 133°04.0′ |
| 47778 | 潮岬(しおのみさき) | 和歌山県東牟婁郡串本町 | 33°27.1′ | 135°45.7′ |
| 47807 | 福岡(ふくおか) | 福岡県福岡市 | 33°35.0′ | 130°23.0′ |
| 47827 | 鹿児島(かごしま) | 鹿児島県鹿児島市 | 31°33.3′ | 130°32.9′ |
| 47909 | 名瀬/本茶峠(なぜ/ふんちゃとうげ) | 鹿児島県奄美市 | 28°23.6′ | 129°33.2′ |
| 47918 | 石垣島(いしがきじま) | 沖縄県石垣市 | 24°20.2′ | 124°09.8′ |
| 47945 | 南大東島(みなみだいとうじま) | 沖縄県島尻郡南大東村 | 25°49.8′ | 131°13.7′ |
| 47971 | 父島(ちちじま) | 東京都小笠原村 | 27°05.7′ | 142°11.1′ |
| 47991 | 南鳥島(みなみとりしま) | 東京都小笠原村 | 24°17.4′ | 153°59.0′ |
| 89532 | 昭和(しょうわ) | 南極昭和基地 | -69°00.3′ | 39°34.7′ |
今回は日本時間2015年9月24日9時の館野(つくば)の高層気象観測データを使って,エマグラムを描画してみたいと思います。
データファイルはこちらで用意しました。新規ファイルを作成し,コピペしてお使いください。以下のコードではファイル名を20150924_09JST_47646.txtとして保存したと仮定して進めます。
# 20150924 09JST 47646
1011.7 26 20.5 83 2.2 30
1000 125 19.1 81 3 52
925 791 15.1 71 2 134
900 1023 13.6 64 2 136
850 1497 10.3 64 4 147
800 2003 10.8 9 6 128
700 3108 7.2 35 3 188
600 4358 -0.3 14 8 166
500 5791 -11.0 67 11 247
400 7503 -17.8 87 12 275
350 8483 -24.1 85 19 258
300 9589 -32.9 76 20 253
250 10845 -43.6 /// 26 259
200 12299 -56.9 /// 33 269
175 13130 -64.3 /// 40 266
150 14066 -64.9 /// 36 278
125 15184 -65.0 /// 27 245
100 16547 -65.1 /// 20 294
70 18710 -61.8 /// 12 260
50 20800 -61.7 /// 6 94
40 22195 -56.4 /// 11 96
30 24037 -52.2 /// 6 150
20 26652 -50.4 /// 4 108
15 28530 -48.9 /// 7 100
10 31212 -44.7 /// 8 147
5 /// /// /// /// ///
ちなみに,下のスクリーンショットに示したように,気象庁のウェブサイトから,地点,観測年,月,日,時間を指定して,データの種類(一番上の「2015年9月24日9時の指定気圧面の観測データを表示」)をクリックすると表形式でデータが表示されます。
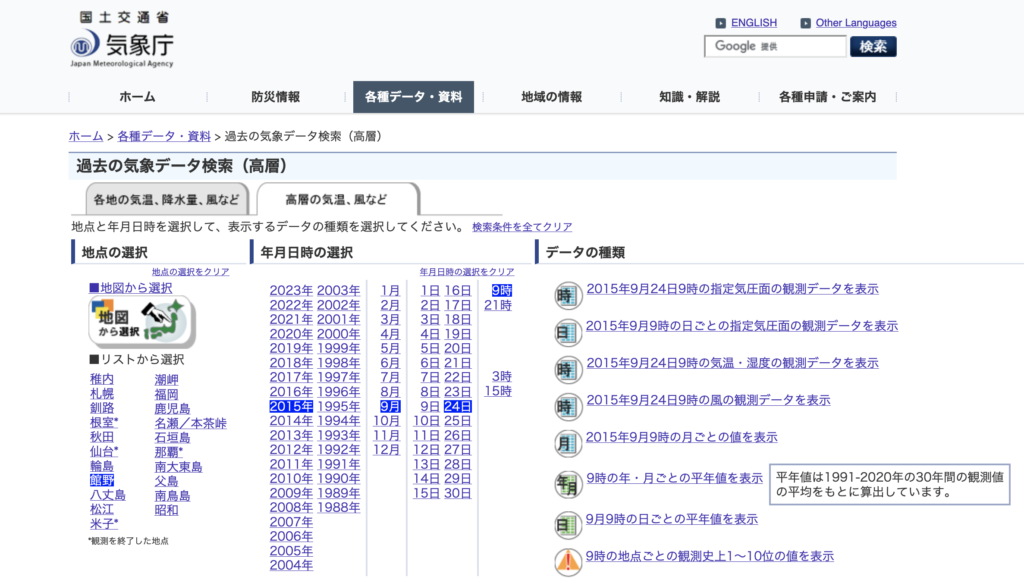
なお,ウェブページのソースコードを解析して上記のようなデータを (半) 自動的に取得する技術をウェブスクレイピングといいます。この技術を使って,データの取得を自動化することもできます。これに関しては,別の記事で紹介します。
高層気象観測データの取得とエマグラムの描画の実装
MetPyを使って,上記のファイルを読み込んで,エマグラムをプロットしてみます。以下に実装例を示します。以下のコードをコピーしてplot-emagram.pyという名前で,適当なディレクトリ(ここでは,~/Desktop/labcode/python/plot-emagram とします)に保存します。上に示したデータファイルも同じディレクトリに入れておきましょう。
import matplotlib.pyplot as plt
import metpy.calc as mpcalc
from metpy.plots import SkewT
from metpy.units import units
import numpy as np
#------------------------------------------------------------------------------
# データを読み込む
fname = "20150924_09JST_47646.txt"
data = np.genfromtxt(fname=fname, unpack=True)
prss = data[0]*units.hPa # 気圧
hght = data[1]*units.meters # ジオポテンシャル高度
tmpr = data[2]*units.degC # 気温
rhmd = data[3] # 相対湿度
wndsp = data[4]*units('m/s') # 風速
wnddr = data[5]*units.degrees # 風向
#------------------------------------------------------------------------------
# --- 計算
# 風速,風向から風の水平成分を計算する。
uwnd, vwnd = mpcalc.wind_components(wndsp, wnddr)
# 気温と相対湿度から露点温度を計算する。
dewp = mpcalc.dewpoint_from_relative_humidity(tmpr, rhmd/100.0)
#------------------------------------------------------------------------------
# *** プロット
# --- プロット範囲の設定
xmax = 40 # 横軸(温度)の最大値
xmin = -90 # 横軸(温度)の最小値
ymin = 100 # 縦軸(気圧)の最小値
ymax = 1020 # 縦軸(気圧)の最大値
# --- 全般の設定
fig = plt.figure(figsize=(210/25.4, 294/25.4), dpi=100)
out_fig_path = 'emagram.png'
skew = SkewT(fig, rotation=0, aspect=150)
# --- 軸の設定
skew.ax.set_xlim(xmin, xmax)
skew.ax.set_ylim(ymax, ymin)
# --- ラベルの設定
skew.ax.set_xlabel('Temperature (℃)')
skew.ax.set_ylabel('Pressure (hPa)')
# --- 気温,露点温度,風の鉛直分布をプロットする
skew.plot(prss, tmpr, 'red')
skew.plot(prss, dewp, 'blue')
skew.plot_barbs(prss, uwnd, vwnd)
# --- 乾燥断熱線のプロット
t0 = np.arange(200, 360, 10)*units.K # プロットする乾燥断熱線のスタート温度
# 乾燥断熱線をプロット
skew.plot_dry_adiabats(t0=t0, lw=0.5, colors='red')
# ラベルを350hPaに付す
for t in t0:
p1 = 350*units.hPa
t1 = mpcalc.dry_lapse(p1, t, 1000*units.hPa) # p1=350hPaまで乾燥断熱線に従って持ち上げたときの温度
if t1 < xmin*units.degC:
continue
skew.ax.text(t1, p1, f'{t.magnitude}', fontsize=9,
horizontalalignment='center', color='red')
# --- 湿潤断熱線のプロット
t0 = np.arange(245, 320, 5)*units.K # プロットする湿潤断熱線のスタート温度
# 湿潤断熱線のプロット
skew.plot_moist_adiabats(t0=t0, lw=0.5, colors='green')
# ラベルを250hPaに付す
for t in t0:
p1 = 250 * units.hPa
t1 = mpcalc.moist_lapse(p1, t, 1000*units.hPa) # p1=250hPaまで湿潤断熱線に従って持ち上げたときの温度
if t1 < xmin*units.degC:
continue
skew.ax.text(t1, p1, f'{t.magnitude}', fontsize=9,
horizontalalignment='center', color='green')
# --- 等飽和混合比線のプロット
# プロットする混合比の値,プロットする気圧の範囲を指定する
mixing_ratio = np.array([0.2, 0.4, 0.6, 1, 2, 4, 5, 10, 15, 20, 25, 30, 35]).reshape(-1, 1) * units('g/kg')
pressure = np.arange(1000, 10, -50)*units.hPa
# 等飽和混合比線のプロット
skew.plot_mixing_lines(mixing_ratio=mixing_ratio, pressure=pressure, lw=0.5, colors='blue')
# ラベルを110hPaに付す
for mr in mixing_ratio.flatten():
p1 = 110 * units.hPa
dewpt = mpcalc.dewpoint(mpcalc.vapor_pressure(p1, mr))
skew.ax.text(dewpt, p1, f'{mr.magnitude}', fontsize=9,
horizontalalignment='center')
#------------------------------------------------------------------------------
# 図の保存
plt.savefig(out_fig_path, transparent=False)プログラムを実行する
ターミナルを開き,
$ cd ~/Desktop/labcode/python/plot-emagram
と入力し,ディレクトリを移動します。あとは以下のコマンドを実行するだけです。( $マークは無視してください)
$ python plot-emagram.py
実行結果
~/Desktop/labcode/python/plot-emagram にemagram.pngというファイルができて,以下のようになっていれば成功です!
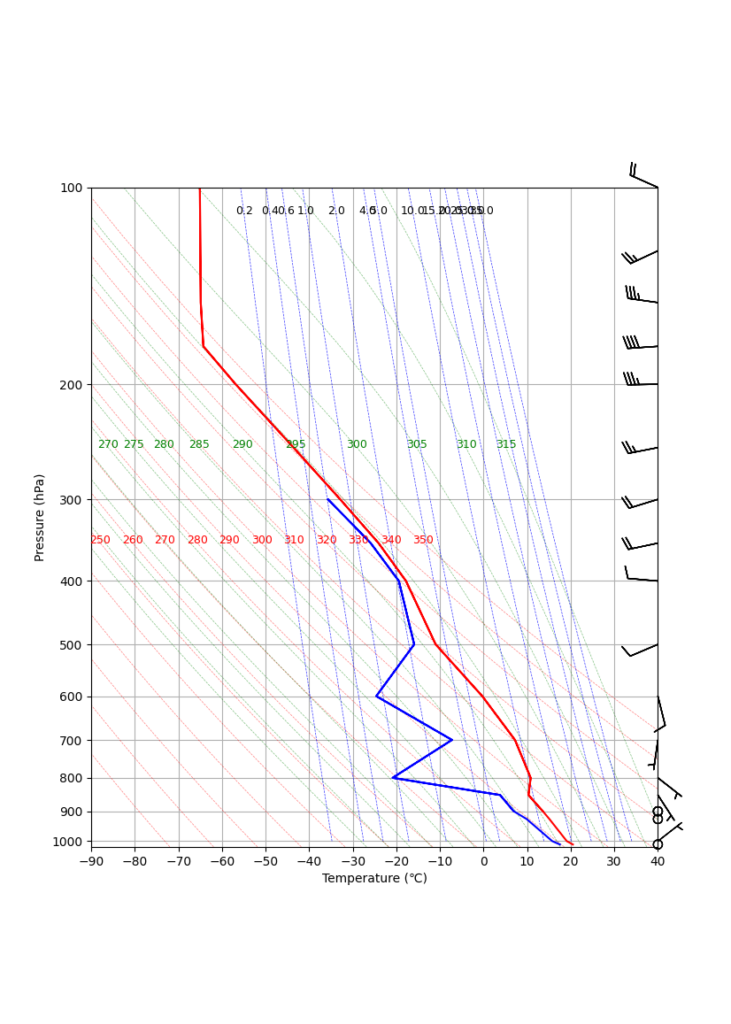
赤の太実線は気温を,青の太実線は露点温度をあらわします。また,赤の点線で乾燥断熱線を,緑の点線で湿潤断熱線を,青の点線で等飽和混合比線を描画しました。
右端には,各高度面における風の水平成分をプロットしています。風向が下から上に向かって時計まわりに変化し,上空では西風が吹いていることがわかります。
コードの解説
上に書いたソースコードの解説をしていきます。
import matplotlib.pyplot as plt
import metpy.calc as mpcalc
from metpy.plots import SkewT
from metpy.units import units
import numpy as npまず,必要なモジュールをインポートします。
#------------------------------------------------------------------------------
# データを読み込む
fname = "20150924_09JST_47646.txt"
data = np.genfromtxt(fname=fname, unpack=True)
prss = data[0]*units.hPa # 気圧
hght = data[1]*units.meters # ジオポテンシャル高度
tmpr = data[2]*units.degC # 気温
rhmd = data[3] # 相対湿度
wndsp = data[4]*units('m/s') # 風速
wnddr = data[5]*units.degrees # 風向次に,データを読み込みます。ファイル名を指定して,np.genfromtxtを使って読み込みます。データファイルに「///」が含まれており,np.loadtxtではエラーが出てしまいます。np.genfromtxtはこのようなデータをはnanとなります。
データファイルには,一列目から順に,気圧,ジオポテンシャル高度,気温,相対湿度,風速,風向のデータが入っています。MetPy の units で単位を付してndarrayに格納します。
#------------------------------------------------------------------------------
# --- 計算
# 風速,風向から風の水平成分を計算する。
uwnd, vwnd = mpcalc.wind_components(wndsp, wnddr)
# 気温と相対湿度から露点温度を計算する。
dewp = mpcalc.dewpoint_from_relative_humidity(tmpr, rhmd/100.0)風速と風向の値から風の水平成分を計算するには,mpcalc.wind_conmpnents(<風速>, <風向>)を使用します。戻り値は東西成分,南北成分です。
気温と相対湿度から露点温度を計算するには,mpcalc.dewpoint_from_relative_humidity(<気温>, <相対湿度>) を使用します。相対湿度は0から1の間の値に変換してから入力しています。
#------------------------------------------------------------------------------
# *** プロット
# --- プロット範囲の設定
xmax = 40 # 横軸(温度)の最大値
xmin = -90 # 横軸(温度)の最小値
ymin = 100 # 縦軸(気圧)の最小値
ymax = 1020 # 縦軸(気圧)の最大値
# --- 全般の設定
fig = plt.figure(figsize=(210/25.4, 294/25.4), dpi=100)
out_fig_path = 'emagram.png'
skew = SkewT(fig, rotation=0, aspect=150)以上で準備が整いましたので,ここからはプロットの準備に取り掛かります。まず,プロット範囲の設定や,サイズ,解像度,出力ファイル名の設定をしておきます。
エマグラムを描画するときは,MetPyのSkewTを使用します。引数の rotation は等温度線が水平軸に対して回転しない(垂直になる)ようにするための指定です。デフォルトは30で30度傾いたものになります。また,aspect は縦軸/横軸のアスペクト比を指定します。デフォルトは80.5でやや横長になります。縦長にしたいので,150としました。
# --- 軸の設定
skew.ax.set_xlim(xmin, xmax)
skew.ax.set_ylim(ymax, ymin)
# --- ラベルの設定
skew.ax.set_xlabel('Temperature (℃)')
skew.ax.set_ylabel('Pressure (hPa)')軸の設定を反映させ,ラベルを付します。縦軸は気圧,横軸は気温です。
# --- 気温,露点温度,風の鉛直分布をプロットする
skew.plot(prss, tmpr, 'red')
skew.plot(prss, dewp, 'blue')
skew.plot_barbs(prss, uwnd, vwnd)気温を赤で,露点温度を青でプロットし,風の水平成分を右端にプロットします。
通常のplotとは違って,第一引数が縦軸,第二引数が横軸ですが,縦軸に対して横軸の値をプロットするものなので,こちらのほうが直感的でしょう。
# --- 乾燥断熱線のプロット
t0 = np.arange(200, 360, 10)*units.K # プロットする乾燥断熱線のスタート温度
# 乾燥断熱線をプロット
skew.plot_dry_adiabats(t0=t0, lw=0.5, colors='red')
# ラベルを350hPaに付す
for t in t0:
p1 = 350*units.hPa
t1 = mpcalc.dry_lapse(p1, t, 1000*units.hPa) # p1=350hPaまで乾燥断熱線に従って持ち上げたときの温度
if t1 < xmin*units.degC:
continue
skew.ax.text(t1, p1, f'{t.magnitude}', fontsize=9,
horizontalalignment='center', color='red')空気塊が飽和せずに上昇したときの線である,乾燥断熱線(赤の点線)をプロットします。便利なものが用意されていて,skew.plot_dry_adiabats() とするだけでプロットすることができます。引数の t0 は描かれる乾燥断熱線のスタート温度です。気象庁のウェブページにある解説図にならって,200Kから360Kの10K刻みでプロットします。
最終段はそれぞれの乾燥断熱線に何Kのものかのラベルを付している部分です。mpcalc.dry_lapse(<気圧面>, <参照気圧面の気温>, <参照気圧面>) とすることで,気圧面まで乾燥断熱線にしたがって空気塊を持ち上げたときの温度を計算してくれます。
# --- 湿潤断熱線のプロット
t0 = np.arange(245, 320, 5)*units.K # プロットする湿潤断熱線のスタート温度
# 湿潤断熱線のプロット
skew.plot_moist_adiabats(t0=t0, lw=0.5, colors='green')
# ラベルを250hPaに付す
for t in t0:
p1 = 250 * units.hPa
t1 = mpcalc.moist_lapse(p1, t, 1000*units.hPa) # p1=250hPaまで湿潤断熱線に従って持ち上げたときの温度
if t1 < xmin*units.degC:
continue
skew.ax.text(t1, p1, f'{t.magnitude}', fontsize=9,
horizontalalignment='center', color='green')この部分は湿潤断熱線(緑の点線)について,乾燥断熱線と同様のことをしている部分です。
# --- 等飽和混合比線のプロット
# プロットする混合比の値,プロットする気圧の範囲を指定する
mixing_ratio = np.array([0.2, 0.4, 0.6, 1, 2, 4, 5, 10, 15, 20, 25, 30, 35]).reshape(-1, 1) * units('g/kg')
pressure = np.arange(1000, 10, -50)*units.hPa
# 等飽和混合比線のプロット
skew.plot_mixing_lines(mixing_ratio=mixing_ratio, pressure=pressure, lw=0.5, colors='blue')
# ラベルを110hPaに付す
for mr in mixing_ratio.flatten():
p1 = 110 * units.hPa
dewpt = mpcalc.dewpoint(mpcalc.vapor_pressure(p1, mr))
skew.ax.text(dewpt, p1, f'{mr.magnitude}', fontsize=9,
horizontalalignment='center')
この部分は等飽和混合比線(青の点線)について,乾燥断熱線と同様のことをしている部分です。
#------------------------------------------------------------------------------
# 図の保存
plt.savefig(out_fig_path, transparent=False)
最後に図を保存して終了です。
最後に
今回は,大気の鉛直構造を把握するためのエマグラムの描画をMetPyで行う方法を紹介しました。エマグラムを用いると,どこまで雲が発達できるかなどといった情報が得られます。また,気象予報士試験で登場する定番の図でもあります。ぜひご活用ください。
参考ウェブサイト
MetPyの公式サイトです。
Pythonでやってみる気象データ解析の技術書を販売中
¥2,500 → ¥1,500 今なら40%OFF!!
気象の勉強をされている方必読!
気象予報士でもある著者がわかりやすく解説
プログラムを公開しているのでお手元で試せます!




