【気象データ】「〇〇年に一度の大雨」の算出 (当てはめる分布関数の解説編)【統計解析】

はじめに

ここ最近、大雨のニュースを見るたびに「〇〇年に一度の大雨」という表現を目にします。これは「千年に一人の美少女」や「百年に一度の逸材」といったレトリックではなく、データに基づいて統計的に算出された根拠のある数字です。

気象庁や自治体では観測結果をもとにこのような量を算出し、発表することで防災に役立てています。このシリーズでは、算出方法を確認し、Pythonを使って、実装・計算してみたいと思います。

なお、ここで紹介する手法は、実際に公的機関が発表しているものとは異なる場合が多分にありますので、十分にご注意ください。

今回は、前回に引き続き、ヒストグラムに当てはめる分布関数について紹介したいと思います。

動作検証済み環境

macOS Monterey 12.6.2, Python 3.9.15, SciPy 1.11.2

Pythonでやってみる気象データ解析の技術書を販売中

¥2,500 → ¥1,500 今なら40%OFF!!

気象の勉強をされている方必読！
気象予報士でもある著者がわかりやすく解説
プログラムを公開しているのでお手元で試せます！

技術書ページへ

「○○年に一度の大雨」の計算方法とは

気象庁は観測結果をもとに、各地点について「〇〇年に一度の降水量」を算出し、発表しています。

ある期間内に1回起こると考えられる降水量のことを確率降水量といいます。気象庁の解説ページでは、確率降水量の推定方法が解説されていますので、これに基づいて「〇〇年に一度の大雨」の値を計算してみたいと思います。

大まかには次のような流れになっています。

年最大日降水量のヒストグラムを作成する
分布関数を当てはめる
分布関数の当てはまり具合を確認する
当てはめた分布関数から確率降水量を算出する

今回は、上記2. の「分布関数を当てはめる」の準備として、当てはめに用いられる分布関数を確認しておきましょう。

当てはめる分布関数の種類

気象庁の解説ページにあるように、当てはめに用いられる分布関数は次の５種類です。

グンベル分布
一般化極値 (GEV) 分布
平方根指数型最大値分布
対数ピアソンⅢ型分布
対数正規分布

今回は、1から3までの分布関数を表す式を確認し、実際にパラメータを変えてプロットしてみて挙動を見てみましょう。

当てはめる分布関数の表式

本記事で言うところの「分布関数」は、確率・統計学では、確率密度関数 (probability density function, PDF) と呼ばれるものです。

5つの確率密度関数の表式を以下に示します。

グンベル (Gumbel, ガンベルとも呼ばれる) 分布

確率密度関数は

$$ f(x) = \frac{1}{\sigma}\exp\left\{-\left(\frac{x-\mu}{\sigma}\right)-\exp\left[-\left(\frac{x-\mu}{\sigma}\right)\right]\right\} $$

と表されます。パラメータは $\sigma$ (Scipyに用意されている gumbel_r では $\texttt{scale}$) と $\mu$ ($\texttt{loc}$) です。

ありがたいことに、Scipyには統計学でよく利用される関数が用意されています。今回利用するのは、これです。

一般化極値 (GEV) 分布

確率密度関数は

$$ f(x) = \frac{1}{\sigma}\exp\left[-\left(1-c\frac{x-\mu}{\sigma}\right)^{1/c}\right]\left(1-c\frac{x-\mu}{\sigma}\right)^{1/c-1} $$

と表されます。パラメータは $\sigma$ ($\texttt{scale}$) と $\mu$ ($\texttt{loc}$) および $c$ です。

一般化極値分布もScipyが用意してくれています (これです)。

平方根指数型最大値分布 (SQRT-ET)

$$ f(x) = \frac{ab}{2}\exp\left[-\sqrt{bx} – a\left(1+\sqrt{bx}\right)\exp\left(-\sqrt{bx}\right)\right] $$

パラメータは $a$、 $b$ です。これは、Scipyにはありません。作ってみましょう。

実装と実行

プログラムの例

パラメータ設定して3つの確率密度関数をプロットするプログラムの例を示します。

import matplotlib.pyplot as plt
import numpy as np

import scipy.stats as ss

# --- パラメータの設定
# - Gumbel分布
scale_gumbel = [1.0, 1.0, 0.5, 2.0]
loc_gumbel = [0.0, 1.0, 0.0, 0.0]

# - 一般化極値 (GEV) 分布
scale_gev = [1.0, 1.0, 0.5, 1.0]
loc_gev = [1.0, 5.0, 1.0, 1.0]
c_gev = [-0.1, -0.1, -0.1, -0.5]

# - 平方根指数型最大値分布
a_sqet = [10.0, 10.0, 5.0, 5.0]
b_sqet = [10.0, 5.0, 10.0, 5.0]

# --- 平方根指数型最大値分布の関数
def sqet(x, a, b):
    f = a*b*0.5*np.exp(-np.sqrt(b*x)-a*(1.0+np.sqrt(b*x))*np.exp(-np.sqrt(b*x)))
    return f

# --- 全般の設定
fig = plt.figure(figsize=(6, 8), dpi=100)

ax01 = fig.add_subplot(3, 1, 1)
ax02 = fig.add_subplot(3, 1, 2)
ax03 = fig.add_subplot(3, 1, 3)

x = np.linspace(-1, 10, 110)
for i in range(len(scale_gumbel)):
    rv = ss.gumbel_r.pdf(x, loc=loc_gumbel[i], scale=scale_gumbel[i])
    ax01.plot(x, rv, label=f"scale={scale_gumbel[i]}, loc={loc_gumbel[i]}")

ax01.legend()

for i in range(len(scale_gev)):
    rv = ss.genextreme.pdf(x, c=c_gev[i], loc=loc_gev[i], scale=scale_gev[i])
    ax02.plot(x, rv, label=f"scale={scale_gev[i]}, loc={loc_gev[i]}, c={c_gev[i]}")   

ax02.legend()

for i in range(len(a_sqet)):
    rv = sqet(x=x[x>=0], a=a_sqet[i], b=b_sqet[i])
    ax03.plot(x[x>=0], rv, label=f"a={a_sqet[i]}, b={b_sqet[i]}")

ax03.legend()

plt.show()

このコードを plot-pdfs.pyとして適当なディレクトリ (ここでは、~/Desktop/labcode/python/probable-precipitationとします。) に保存します。

プログラムを実行する

ターミナルを開き、

$ cd ~/Desktop/labcode/python/probable-precipitation

と入力し、ディレクトリを移動します（ $マークは無視してください）。つぎに、プログラムを実際に実行しましょう。

$ python plot-pdfs.py

とします。次のようなウィンドウが立ち上がれば成功です。

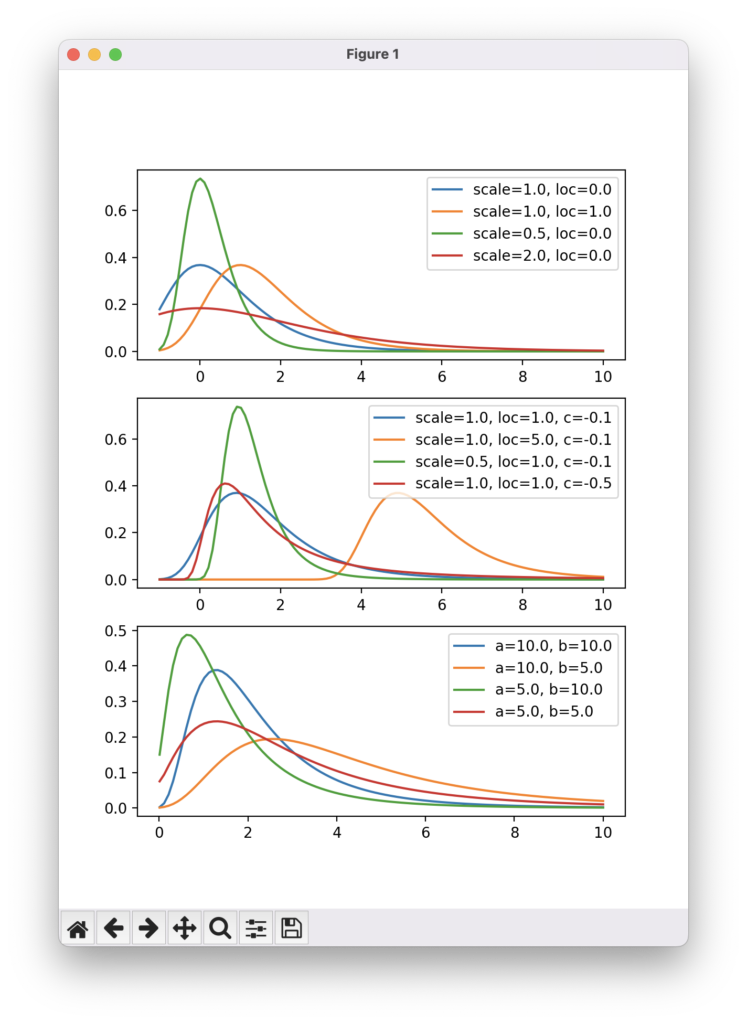
一番上がグンベル分布、二番目が一般化極値分布、三番目が平方根指数型最大値分布で、凡例にパラメータを示しています。以前の記事で年最大日降水量のヒストグラムで見たような、右に裾の長い分布を表現できます。

コードの解説

上で紹介したコードの解説をします。

import matplotlib.pyplot as plt
import numpy as np

import scipy.stats as ss

まず、必要なモジュールをインポートします。今回肝となるscipy.statsはssという名前のオブジェクトとしてインポートしておきます。

# --- パラメータの設定
# - Gumbel分布
scale_gumbel = [1.0, 1.0, 0.5, 2.0]
loc_gumbel = [0.0, 1.0, 0.0, 0.0]

# - 一般化極値 (GEV) 分布
scale_gev = [1.0, 1.0, 0.5, 1.0]
loc_gev = [1.0, 5.0, 1.0, 1.0]
c_gev = [-0.1, -0.1, -0.1, -0.5]

# - 平方根指数型最大値分布
a_sqet = [10.0, 10.0, 5.0, 5.0]
b_sqet = [10.0, 5.0, 10.0, 5.0]

確率密度関数のパラメータを設定しています。この辺りはご自身で変えてみて、どのように変化するか確かめてみてください。

# --- 平方根指数型最大値分布の関数
def sqet(x, a, b):
    f = a*b*0.5*np.exp(-np.sqrt(b*x)-a*(1.0+np.sqrt(b*x))*np.exp(-np.sqrt(b*x)))
    return f

平方根指数型最大値分布の関数を定義しています。上で述べた式をpythonの形式に書き換えただけです。

# --- 全般の設定
fig = plt.figure(figsize=(6, 8), dpi=100)

ax01 = fig.add_subplot(3, 1, 1)
ax02 = fig.add_subplot(3, 1, 2)
ax03 = fig.add_subplot(3, 1, 3)

プロットの設定です。3つの枠を縦に並べます。

x = np.linspace(-1, 10, 110)
for i in range(len(scale_gumbel)):
    rv = ss.gumbel_r.pdf(x, loc=loc_gumbel[i], scale=scale_gumbel[i])
    ax01.plot(x, rv, label=f"scale={scale_gumbel[i]}, loc={loc_gumbel[i]}")

ax01.legend()

for i in range(len(scale_gev)):
    rv = ss.genextreme.pdf(x, c=c_gev[i], loc=loc_gev[i], scale=scale_gev[i])
    ax02.plot(x, rv, label=f"scale={scale_gev[i]}, loc={loc_gev[i]}, c={c_gev[i]}")   

ax02.legend()

for i in range(len(a_sqet)):
    rv = sqet(x=x[x>=0], a=a_sqet[i], b=b_sqet[i])
    ax03.plot(x[x>=0], rv, label=f"a={a_sqet[i]}, b={b_sqet[i]}")

ax03.legend()

確率密度関数をプロットしていきます。パラメータの組がいくつかあるので、その数だけ for でループさせます。

まず、x = np.linspace(-1, 10, 110) で-1から10までの110点の等間隔数列を用意します。この点に対して関数の値を計算します。

一番上のfor文はGumbel分布のものです。ss.gumbel_r.pdf(x)とすると、xに対するGumbel分布の確率密度の値を返してくれます。パラメータであるlocとscaleはコードにあるように与えれば良いです。これをax01.plot() に渡すと一段目にプロットしてくれます。ax01.legend()は凡例を書かせるために必要です。

二段目のfor文は一般化極値分布、三段目が平方根指数型最大値分布のもので、同様の操作をしています。三段目でx[x>=0]としているのは、平方根指数型最大値分布の定義域が $x\ge0$ であるからです。