本記事では、偏微分方程式の数値解法の基本を、分かりやすい具体例とともに掘り下げていきます。偏微分方程式には解析的な解が存在しない場合が多いため、Pythonを活用してこれらの複雑な問題にアプローチする方法を学びます。
本記事を足がかりに数値解析の旅を始めてみませんか?
注1) 本記事は丁寧に解説しすぎたあまり、大変長くなっております。まずはご自身が興味のある部分だけをお読みいただくことを推奨します。
注2) 差分法の一部の話だけにとどめています。誤差や境界条件などの詳細な議論は冗長化を避けるためにご紹介していません。
macOS Monterey(12.7.1), python3.11.4
Pythonで学ぶ偏微分方程式の数値シミュレーションの技術書を販売中
¥2,500 → ¥1,000 今なら60%OFF!!
計算方法、グラフやアニメーションの作成方法、計算ログの残し方を惜しみなく解説しています!
理論と実装の溝を埋めてくれる良書です!
偏微分方程式の数値解法とは
偏微分方程式の数値解法は、偏微分方程式(PDE: Partial Differential Equations)の解を近似的に求めるための手法のことを指します。これらの方程式は、多くの場合、解析的な解が見つけられないため、数値的な手法が必要となります。以下に、主な数値解法をいくつか紹介します。
- 有限差分法(Finite Difference Method): 空間や時間を離散的なグリッドに分割し、微分を差分に置き換えることにより近似します。この方法は直感的で実装が比較的簡単ですが、グリッドの選択が解の精度に大きく影響します。
- 有限要素法(Finite Element Method): 問題の領域を小さな「要素」に分割し、各要素内で方程式を近似します。この方法は複雑な形状や境界条件を持つ問題に適しています。
- 有限体積法(Finite Volume Method): 保存則を基にした方程式に特に適しており、領域を小さな「体積」に分割し、各体積内の平均値を計算します。
- スペクトル法(Spectral Method): 方程式を異なる周波数の波形の和として表し、これらの波形の係数を計算することで解を近似します。高い精度を達成できますが、滑らかな解が必要です。
- 差分時間領域法(Finite-Difference Time-Domain, FDTD): 電磁気学で広く使われている、時間領域における有限差分法の一種です。
これらの方法は、物理学、工学、気象学など様々な分野で偏微分方程式の解を求めるために用いられます。それぞれの方法には特徴や適用できる問題の種類が異なり、問題の性質に応じて最適な方法を選択する必要があります。また、高度なコンピュータシミュレーションにおいては、これらの方法が組み合わされることもあります。
本記事では有限差分法(Finite Difference Method)を用いた数値解法についてご紹介します。
差分近似
偏微分方程式の数値解法においては差分法は非常に多く用いられます。
差分法では差分近似を用います。まずは常微分係数の差分近似の考え方を復習し、次に偏微分係数での差分近似の考え方を学習しましょう。
常微分係数の差分近似
偏微分方程式の差分近似も接線の勾配を曲線上の近接2点間の勾配で近似する常微分係数の差分と本質的には全く同じです。
$x$軸上の点 $x_{i-1} < x_{i} < x_{i+1}$ ($x_{i+1}-x_{i} = x_{i}-x_{i-1}= \Delta x$ とします)に対する曲線 $y=y(x)$上の3点を($x_{i-1},y_{i-1}$),($x_{i},y_{i}$),($x_{i+1},y_{i+1}$)とします。この曲線上の点($x_{i},y_{i}$)における接線の勾配$\tan{\theta}$(接線と$x$軸とのなす角を$\theta$とします)は
$$ \tan{\theta}=\frac{dy}{dx}=\lim_{\Delta x → 0}\frac{\Delta y}{\Delta x} = \lim_{\Delta x → 0}\frac{y_{i+1}-y_{i}}{\Delta x} $$
なので、$\Delta x$が十分小さければ$\tan{\theta} \fallingdotseq (y_{i+1} – y_{i})/\Delta x$と近似できます。すなわり、常微分係数 $dy/dx$が次式で近似できることになります。
$$ \frac{dy}{dx} \fallingdotseq \frac{y_{i+1} – y_{i}}{\Delta x} $$
これが前進差分近似です。
同様に$\tan{\theta} \fallingdotseq (y_{i} – y_{i-1})/\Delta x$と近似することもできるので、
$$ \frac{dy}{dx} \fallingdotseq \frac{y_{i} – y_{i-1}}{\Delta x} $$
と表すこともできます。これは後退差分近似です。
さらに、$\tan{\theta} \fallingdotseq (y_{i+1} – y_{i-1})/ 2\Delta x$と近似すると
$$ \frac{dy}{dx} \fallingdotseq \frac{y_{i+1} – y_{i-1}}{2\Delta x} $$
となり、これは中心差分近似です。偏微分方程式についても考え方は全く同様です。
偏微分係数の差分近似
$u = u(x,y)$ が領域 $0 \leqq x \leqq a, 0 \leqq y \leqq b$ で与えられているものとします。この領域を以下の図のように格子(差分格子)に分割します。格子間隔は等間隔でもよいですが、一般的には図のように不等間隔格子を用いてもよいです。
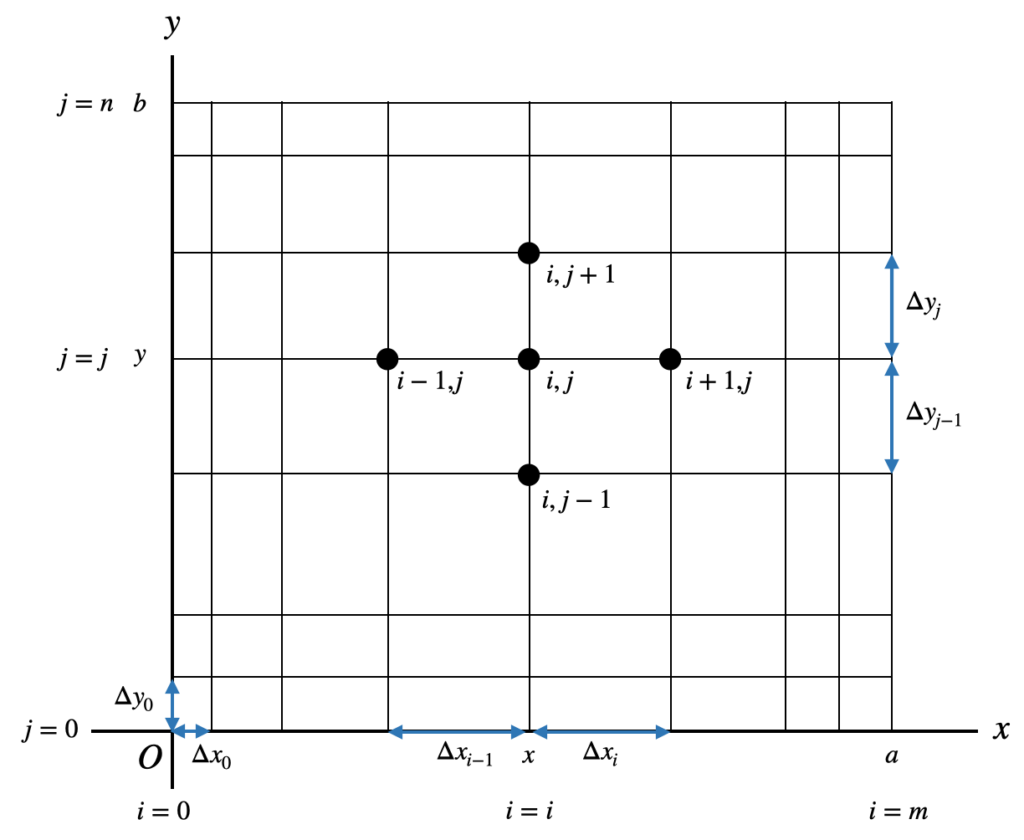
$x$方向への格子番号を $i=0 \sim m$ 、$y$方向格子番号を$j=0 \sim n$とします。点$(x,y)$の格子点の番号を図に示したように $(i,j)$ とし、そこでの $u$ の値 $u(x,y)$ を $u_{i,j}$ と表します。格子点 $(i,j)$ の隣の格子点は図に示したように $\Delta x_i,\Delta y_i$ などで表しておきます。そうすると偏微分系数 $∂u/∂x, ∂u/∂y$ に対する差分近似は、 $∂u/∂x$ に対しては $j$ を固定し、 $∂u/∂y$ に対しては $i$ を固定して次のように表されます。
前進差分近似だと
$$ \begin{aligned} \frac{∂u}{∂x} = \frac{u_{i+1, j} – u_{i, j}}{\Delta x_i} \\ \frac{∂u}{∂y} = \frac{u_{i, j+1} – u_{i, j}}{\Delta y_i} \end{aligned} $$
後退差分近似だと
$$ \begin{aligned} \frac{∂u}{∂x} = \frac{u_{i, j} – u_{i-1, j}}{\Delta x_i} \\ \frac{∂u}{∂y} = \frac{u_{i, j} – u_{i, j-1}}{\Delta y_i} \end{aligned} $$
中心差分近似だと
$$ \begin{aligned} \frac{∂u}{∂x} = \frac{u_{i+1, j} – u_{i-1, j}}{\Delta x_{i-1} + \Delta x_i} \\ \frac{∂u}{∂y} = \frac{u_{i, j+1} – u_{i, j-1}}{\Delta y_{i-1} + \Delta y_i} \end{aligned} $$
2階偏微分係数は、たとえば中心差分近似を用いると $∂^2u / ∂x∂y$ は次のように表されます。
$$ \frac{∂^2u}{∂x∂y}=\frac{∂}{∂x} \Big( \frac{∂u}{∂y} \Big) =\frac{(∂u/∂y)_{i+1,j} – (∂u/∂y)_{i-1,j}}{\Delta x_{i-1} + \Delta x_{i}} $$
$(∂u/∂y)_{i+1,j}$ は $i+1$ を固定して $u$ の(中心)差分をとればよいので
$$
\Big( \frac{∂u}{∂y} \Big)_{i+1,j} = \frac{u_{i+1,j+1} – u_{i+1,j-1}}{\Delta y_{i-1} + \Delta y_{i}}
$$
同様に$(∂u/∂y)_{i-1,j}$ は $i-1$ を固定して
$$
\Big( \frac{∂u}{∂y} \Big)_{i-1,j} = \frac{u_{i-1,j+1} – u_{i-1,j-1}}{\Delta y_{i-1} + \Delta y_{i}}
$$
よって、
$$
\frac{∂^2u}{∂x∂y}=\frac{u_{i+1, j+1} – u_{i+1, j-1} – u_{i-1, j+1} + u_{i-1, j-1}}{(\Delta x_{i-1} + \Delta x_{i})(\Delta y_{i-1} + \Delta y_{i})}
$$
となります。 $∂^2u/∂x^2$ と $∂^2u/∂y^2$ に対しては $∂u/∂x$ と $∂u/∂y$ の前進差分を用いて
$$
\frac{∂^2u}{∂x^2}=\frac{∂}{∂x} \Big( \frac{∂u}{∂x} \Big) =\frac{(∂u/∂x)_{i+1,j} – (∂u/∂x)_{i,j}}{\Delta x_{i}}
$$
$(∂u/∂x)_{i+1,j}$ と $(∂u/∂x)_{i,j}$ には後退差分を用いて
$$
\Big( \frac{∂u}{∂x} \Big)_{i+1,j} = \frac{u_{i+1,j} – u_{i,j}}{\Delta x_{i}}, \ \ \ \ \ \ \Big( \frac{∂u}{∂x} \Big)_{i,j} = \frac{u_{i,j} – u_{i-1,j}}{\Delta x_{i-1}}
$$
と表すと
$$
\frac{∂^2u}{∂x^2}=\Big( \frac{u_{i+1,j} – u_{i,j}}{\Delta x_{i}} – \frac{u_{i,j} – u_{i-1,j}}{\Delta x_{i-1}} \Big) \Big/ \Delta x_{i}
$$
と差分化されます。同様にして次式が得られます。
$$
\frac{∂^2u}{∂y^2}=\Big( \frac{u_{i,j+1} – u_{i,j}}{\Delta y_{i}}
\frac{u_{i,j} – u_{i,j-1}}{\Delta y_{i-1}} \Big) \Big/ \Delta y_{i}
$$
格子間隔が等間隔の場合は
$$
\begin{aligned}
\Delta x_{i-1} = \Delta x_{i} =h \\
\Delta y_{i-1} = \Delta y_{i} =k
\end{aligned}
$$
とおくと、これらの上式を $h$ と $k$ で置き換えればよいです。中心差分で求めた結果を示すと次のようになります。
$$
\begin{aligned}
\frac{∂u}{∂x} = \frac{1}{2h}(u_{i+1,j} – u_{i-1,j}) \\
\frac{∂u}{∂y} = \frac{1}{2k}(u_{i,j+1} – u_{i,j-1})
\end{aligned}
$$
2階偏微分係数は次のようになります。
$$
\begin{align*}
\frac{∂^2u}{∂x∂y} &= \frac{1}{4hk}(u_{i+1,j+1} – u_{i+1,j-1} – u_{i-1,j+1} + u_{i-1,j-1}) \\
\frac{∂^2u}{∂x^2} &= \frac{1}{h^2}(u_{i+1,j} – 2u_{i,j} + u_{i-1,j}) \\
\frac{∂^2u}{∂y^2} &= \frac{1}{k^2}(u_{i,j+1} – 2u_{i,j} + u_{i,j-1})
\end{align*}
$$
有限差分法(Finite Difference Method)を用いた数値解法
有限差分法を用いた偏微分方程式を数値的に解く手順としては、
- 偏微分方程式→差分方程式へ変換
- 差分方程式を使って、各要素の値を計算していく
となります。以下でそれぞれの手順について説明します。
偏微分方程式→差分方程式へ変換
ラプラス方程式
$$
\frac{∂^2u}{∂x^2} + \frac{∂^2u}{∂y^2} = 0; \ \ \ \ \ \ 0 \leqq x \leqq a, 0 \leqq y \leqq b \ \ \ \ (1)
$$
を境界条件
$$
u(0,y) = p(y), \ \ \ u(a,y) = q(y), \ \ \ u(x,0) = v(x), \ \ \ u(x,b) = w(x)
$$
のもとで解く場合を例に考えます。($a, b, p,q,v,w$ は既知とします)
まずは式 $(1)$ を差分方程式で表していきましょう。差分方程式への変換は前節の差分近似した偏微分係数を流用します。すなわち
$$
\frac{(u_{i+1,j} – 2u_{i,j} + u_{i-1,j}) }{h^2} + \frac{(u_{i,j+1} – 2u_{i,j} + u_{i,j-1}) }{k^2} = 0
$$
となります。これより、 $u_{i,j}$ を求めると
$$
u_{i,j}=\frac{1}{2(h^2+k^2)} \{k^2(u_{i+1,j} + u_{i-1,j}) + h^2(u_{i,j+1} + u_{i,j-1})\} \ \ \ \ (2)
$$
となります。
差分方程式を使って、各要素の値を計算していく
$u_{i,j}$ の差分方程式をよく眺めてみましょう。
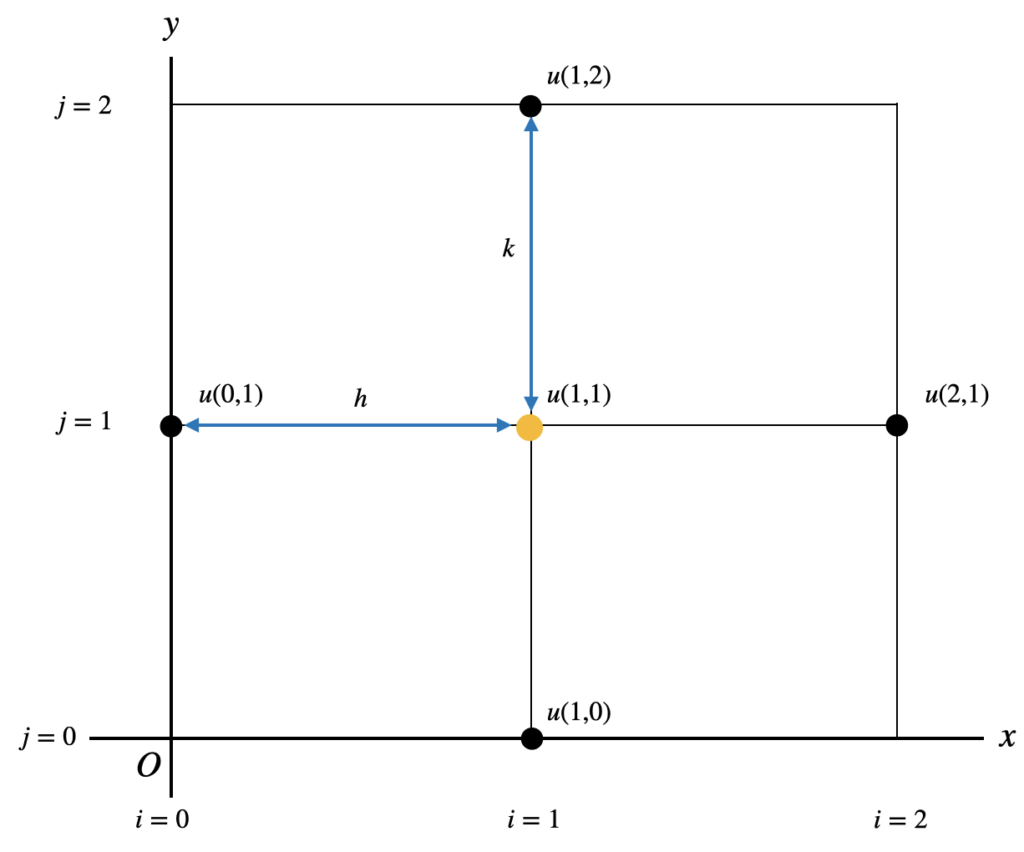
たとえば、 $u_{1,1}$ を求めたいとき、上式 $(2)$ を用いると
$$
u_{1,1}=\frac{1}{2(h^2+k^2)} \{k^2(u_{2,1} + u_{0,1}) + h^2(u_{1,2} + u_{1,0})\}
$$
となります。下の図にも表しましたが $u_{2,1}, u_{0,1}, u_{1,2}, u_{1,0}$ が既知であれば $u_{1,1}$ は求められることがわかります。ある格子点における $u$ の値は前後左右の格子点の$u$ 値から計算できるのです。
境界上における $u$ の値 $p(y),q(y),v(x),w(x)$ は既知なので、それ以外の $u_{i,j}(i=1,2, …, m-1;j=1,2, …, n-1)$ に適当な初期値、たとえば $u_{i,j}=0$ を与えておきます。この初期値を $(2)$ 式に代入し、新しい $u_{i,j}^{(1)}$ を求めます。次に$u_{i,j}^{(1)}$ を $(2)$ 式に代入して次の値 $u_{i,j}^{(2)}$ を求めます。このような操作を繰り返して、第 $k$ と第 $k+1$ 近似値の相対誤差が、指定した十分小さな $\epsilon$ の値より小さくなったとき、すなわち
$$
|(u_{i,j}^{(k+1)} – u_{i,j}^{(k)}) / u_{i,j}^{(k+1)}| \leqq \epsilon; \ \ \ \ i=1,2, …, m-1; \ \ j=1,2, …, n-1;
$$
となったとき解は収束したものとみなして、$u_{i,j}^{(k+1)}$ を解とします。しかしながら、格子点が多くなると判定すべき解 $u_{i,j}$ が多くなり、収束判定に時間を要します。
その場合収束判定の時間を軽減する1つの方法として、すべての解の収束を同時に判定する方法が挙げられます。どういうことかというと、誤差の合計の相対量を用いて
$$
\sum_{i=1}^{m-1}\sum_{j=1}^{n-1} \Big|u_{i,j}^{(k+1)} – u_{i,j}^{(k)} \Big| \Big/ \sum_{i=1}^{m-1}\sum_{j=1}^{n-1}\Big|u_{i,j}^{(k+1)}\Big| \leqq \epsilon
$$
によって収束を判定することができます。
なお、 式 $(2)$ で繰り返し計算を行う場合、 $u$ の値としては最も新しい値を用いると収束が早くなります。ですので、第 $k+1$ 近似解を求める場合すでに求まった $u_{i,j}^{(k+1)}$ があればその値を用います。したがって、式 $(2)$ の反復公式は次のように表されます。
$$
u_{i,j}^{(k+1)}=\frac{1}{2(h^2+k^2)} \{k^2(u_{i+1,j}^{(k)} + u_{i-1,j}^{(k+1)}) + h^2(u_{i,j+1}^{(k)} + u_{i,j-1}^{(k+1)})\} \ \ \ \ (3)
$$
この $(3)$ 式を用いる反復法をガウス-ザイデル法といいます。本記事ではガウス-ザイデル法を用いた数値解法の具体的な事例を以下でご紹介します。
例題
各辺の長さが $1$ の正方形の板で3辺の温度が $0$ 、残りの1辺が $f(x)=4x(1-x)$ の温度につねに保たれているものとする。板内の温度分布を求めよ。
この問題に対する基礎方程式は2次元のラプラス方程式($u(x,y)$ を温度とします)となり、境界条件とともに示すと以下のようになります。
$$
\frac{∂^2u}{∂x^2} + \frac{∂^2u}{∂y^2} = 0; \ \ \ \ \ \ 0 \leqq x \leqq 1, 0 \leqq y \leqq 1
$$
$$
u(0,y) = 0, \ \ \ u(1,y) = 0, \ \ \
u(x,0) = 0, \ \ \ u(x,1) = 4x(1-x)
$$
格子番号を $i=0 \sim m, j=0 \sim n$ とし、任意格子点の $u$ の値を $u_{i,j}$ とします。
上でもご紹介したように、まずはこの偏微分方程式を差分方程式に変換し、次に差分方程式を解くためのプログラムを実装していきましょう。
実装方法
コードは以下のように実装できます。
グラフの作成、結果のテキストファイル出力もしているので少しコードが長いですが、重要な部分は calculate_equation 関数になります。
以下の実装を main.py という名前でどこかのフォルダ(ここでは~/Desktop/labcode/python/numerical_calculation/elliptic_equation とします)に保存しましょう。
import matplotlib.pyplot as plt
import numpy as np
def _set_initial_condition(
*,
array_2d: list,
grid_counts_x: int,
grid_counts_y: int,
) -> None:
"""
初期条件の設定
境界以外のU値を全て0.0001とおく
"""
for j in range(1, grid_counts_y):
for i in range(1, grid_counts_x):
array_2d[i][j] = 0.0001
def _set_boundary_condition(
*,
array_2d: list,
grid_counts_x: int,
grid_counts_y: int,
grid_space: float,
) -> None:
"""境界条件の設定"""
# y=0上の境界条件
for i in range(grid_counts_x + 1):
array_2d[i][0] = 0.0
# y=M上の境界条件
for i in range(grid_counts_x + 1):
array_2d[i][grid_counts_y] = (
4 * (grid_space * i) * (1.0 - grid_space * i)
)
def _is_converged(*, U: list, UF: list, M: int, N: int) -> bool:
"""
収束判定を行う
誤差の合計の相対量がERROR_CONSTANT以下になったら収束と判定する
"""
ERROR_CONSTANT: float = 0.0001 # 精度定数
sum: float = 0.0 # 誤差の初期値
sum0: float = 0.0
for j in range(1, N):
for i in range(1, M):
sum0 += abs(U[i][j])
sum += abs(U[i][j] - UF[i][j])
sum = sum / sum0
return sum <= ERROR_CONSTANT
def calculate_equation(*, M: int, N: int, H: float, MK: int) -> (list, int):
"""
差分方程式を計算する
本プログラムの肝となる関数
"""
# U値のリスト
U: list = [[0.0 for _ in range(M + 1)] for _ in range(N + 1)]
# U値のリスト(精度判定用)
UF: list = [[0.0 for _ in range(M + 1)] for _ in range(N + 1)]
# 初期値設定
_set_initial_condition(
array_2d=U,
grid_counts_x=M,
grid_counts_y=N,
)
_set_boundary_condition(
array_2d=U,
grid_counts_x=M,
grid_counts_y=N,
grid_space=H,
)
# 計算
calc_count: int = 0
for _ in range(MK):
for j in range(1, N):
for i in range(1, M):
UF[i][j] = U[i][j] # 収束判定に必要なため、UをUFにコピー
U[i][j] = (
U[i + 1][j] + U[i - 1][j] + U[i][j + 1] + U[i][j - 1]
) / 4.0
calc_count += 1
# 収束判定
if _is_converged(U=U, UF=UF, M=M, N=N):
print("収束しました")
break
return U, calc_count
def color_plot(
*,
array_2d: list,
grid_counts: int,
grid_space: float,
) -> None:
"""
2次元カラープロット
array_2dのi行j列のままimshowでプロットすると、
原点が左上、横軸が右向き、縦軸が下向きになる。
そこで、array_2dをx軸、y軸としてプロットするために、
転置してからorigin="lower"で縦軸を上向きにしてプロットする。
"""
# グラフの軸の範囲を指定
min_x_y = 0.0 - grid_space / 2
max_x_y = grid_space * grid_counts + grid_space / 2
extent=(min_x_y, max_x_y, min_x_y, max_x_y)
# 2次元配列を転置
array_2d = np.array(array_2d).T
plt.imshow(
array_2d,
cmap="viridis",
interpolation="none",
aspect="auto",
origin="lower",
extent=extent,
)
plt.colorbar()
plt.savefig("./2d_color_plot.png", format="png")
def output_result_file(
array_2d: list,
grid_counts_x: int,
grid_counts_y: int,
grid_space: float,
calc_count: int,
) -> None:
"""2次元配列をテキストファイルに書き出す"""
with open("./calculated_result.txt", "w") as file:
file.write(f"# This file shows calculated result as below.\n\n")
file.write(f"# Calculation Parameters.\n")
file.write(f"grid_counts_x: {grid_counts_x}\n")
file.write(f"grid_counts_y: {grid_counts_y}\n")
file.write(f"grid_space: {grid_space}\n")
file.write(f"calculation_count: {calc_count}\n\n")
file.write(f"# Calculated Matrix H.\n")
for row in array_2d:
line = " ".join(map(str, row))
file.write(line + "\n")
if __name__ == "__main__":
"""
楕円形方程式の数値解法(ガウス-ザイデル法)
grid_counts_x = grid_counts_y の前提で実装をしている
grid_spaceは刻み幅であり、grid_space = 1 / grid_counts_x となる
"""
grid_counts_x: int = 10 # 格子点番号mの値
grid_counts_y: int = 10 # 格子点番号nの値
grid_space: float = 0.1 # 刻み幅
total_calc_count: int = 1000 # 総計算回数
array_2d, calc_count = calculate_equation(
M=grid_counts_x,
N=grid_counts_y,
H=grid_space,
MK=total_calc_count,
)
color_plot(
array_2d=array_2d,
grid_counts=grid_counts_x,
grid_space=grid_space,
)
output_result_file(
array_2d=array_2d,
grid_counts_x=grid_counts_x,
grid_counts_y=grid_counts_y,
grid_space=grid_space,
calc_count=calc_count,
)プログラムを実行する
ターミナルを開き、
$ cd Desktop/labcode/python/numerical_calculation/elliptic_equationと入力し、ディレクトリを移動します。あとは以下のコマンドを実行するだけです。( $マークは無視してください)
$ python main.py実行結果
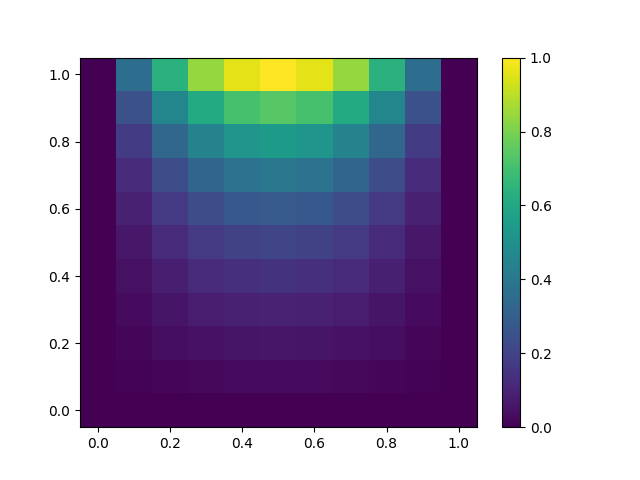
~/Desktop/LabCode/python/numerical_calculation/elliptic_equation に2d_color_plot.pngというファイルができて,以下のような図になっていれば成功です!
境界の温度がじわじわ広がっている様子が可視化されていますね。 $y=1$ の境界上では $4x(1-x)$ に基づいた温度分布をしており、境界以外の分布はラプラス方程式に基づいた温度分布になっています。 このFig. でマスとして色づいて表示されているのものは、定義の上では格子点ですので、そのことは理解した上で図を眺めてください。
また、 calculated_result.txt というテキストファイルも以下のように作成されているはずです。今回は簡単な情報しか出力していませんが、このように計算結果と計算に用いたパラメータを出力しておくことで、第三者でも計算結果を評価することが可能になります。自分のためにも、他の人のためにも、ぜひ結果は出力する癖をつけましょう。
# This file shows calculated result as below.
# Calculation Parameters.
grid_counts_x: 10
grid_counts_y: 10
grid_space: 0.1
calculation_count: 70
# Calculated Matrix H.
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
0.0 0.008929031616324612 0.018753985587845273 0.03045645155113031 0.045215630200268656 0.06454923902703041 0.09052691584655263 0.12614272692516448 0.176072856491503 0.24847942773093906 0.36000000000000004
0.0 0.01698198799554465 0.03566140261199987 0.05789421689302395 0.0858976328737752 0.12249382757113862 0.17145009762302302 0.23799771175707277 0.32968623257237084 0.4578514986882389 0.6400000000000001
0.0 0.023368460401624713 0.04906242166685223 0.07961842109132274 0.11804753163349524 0.1681365089053069 0.23483228099737163 0.3247502516018773 0.44684690227830404 0.6132490318574787 0.8400000000000001
0.0 0.02746745619852549 0.057658441258696666 0.0935383066055323 0.1386104193192113 0.19724196923107878 0.27505222681215186 0.3793696506354582 0.519730238272764 0.708307450428056 0.96
0.0 0.02888372196913288 0.060626251326013327 0.09833879795793664 0.14569078617968717 0.20724196857771687 0.28882793868670115 0.3979934782131962 0.5444261214543008 0.7402602555170518 1.0
0.0 0.02748059290857848 0.05768220659138331 0.09356941707013768 0.1386452033228391 0.19727675460305522 0.27508369154227 0.37939510680256094 0.5197478283548784 0.7083162455407579 0.96
0.0 0.023390838059342566 0.04910290459911079 0.07967141605927938 0.11810678428463689 0.16819576389806784 0.23488587946502332 0.3247936148115438 0.4468768660372461 0.6132640138588368 0.8399999999999999
0.0 0.017006426661918712 0.03570561407859771 0.05795209278737131 0.0859623428147862 0.12255854008880909 0.1715086326507498 0.238045068840605 0.3297189560804824 0.45786786057508466 0.6399999999999999
0.0 0.008946212816146909 0.01878506773578349 0.030497140267083136 0.045261123502502935 0.06459473415967246 0.09056806800477205 0.12617602060802796 0.1760958622623825 0.2484909307093668 0.35999999999999993
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0コードの解説
このPythonコードは、楕円形方程式の数値解法に関するもので、特定の条件下で方程式の近似解を計算し、その結果をグラフとテキストファイルに出力するものです。コードは以下に記すいくつかの主要な部分に分かれています:
1. Pythonにおけるメイン実行ブロック
if __name__ == "__main__":
"""
楕円形方程式の数値解法(ガウス-ザイデル法)
grid_counts_x = grid_counts_y の前提で実装をしている
grid_spaceは刻み幅であり、grid_space = 1 / grid_counts_x となる
"""
grid_counts_x: int = 10 # 格子点番号mの値
grid_counts_y: int = 10 # 格子点番号nの値
grid_space: float = 0.1 # 刻み幅
total_calc_count: int = 1000 # 総計算回数
array_2d, calc_count = calculate_equation(
M=grid_counts_x,
N=grid_counts_y,
H=grid_space,
MK=total_calc_count,
)
color_plot(
array_2d=array_2d,
grid_counts=grid_counts_x,
grid_space=grid_space,
)
output_result_file(
array_2d=array_2d,
grid_counts_x=grid_counts_x,
grid_counts_y=grid_counts_y,
grid_space=grid_space,
calc_count=calc_count,
)
このコードは、Pythonにおけるメイン実行ブロック(if __name__ == "__main__")の中に記述されており、楕円形方程式の数値解法を実装するスクリプトの主要部分を構成しています。Pythonのプログラムが実装されると、まずこの実行ブロック内のコードが実行されます。
ここでは、ガウス-ザイデル法を用いて数値解を計算し、その結果をプロットおよびファイルに出力するプロセスが定義されています。以下に各ステップを詳しく説明します。
処理の流れ
1. パラメータの設定
grid_counts_xとgrid_counts_y: これらは計算に使用される差分格子を定義します。ここでは、両方とも10に設定されており、10×10の格子になります。格子点数としては、11×11 になります。grid_space: これは格子点間の間隔(刻み幅)を定義します。ここでは0.1に設定されています。これは、grid_space = 1 / grid_counts_xの関係に基づいており、均一な格子間隔を保証します。total_calc_count: これは計算の総反復回数を定義します。この例では1000に設定されています。
2. 数値解の計算
calculate_equation関数は、指定されたパラメータ(格子点数、刻み幅、計算回数)を用いて楕円形方程式の数値解を計算します。- この関数は、計算された2次元配列(数値解)と実際の計算回数を返します。
3. 結果の可視化
color_plot関数は、計算された2次元配列をカラープロットとして可視化します。- プロットは
array_2dを元に作成され、grid_counts_xとgrid_spaceを用いて適切な軸の範囲を設定します。
4. 結果のファイル出力
output_result_file関数は、計算結果としての2次元配列をテキストファイルに出力します。- ファイルには、計算パラメータと計算結果が含まれます。
2. 差分方程式の計算
def calculate_equation(*, M: int, N: int, H: float, MK: int) -> (list, int):
"""
差分方程式を計算する
本プログラムの肝となる関数
"""
# U値のリスト
U: list = [[0.0 for _ in range(M + 1)] for _ in range(N + 1)]
# U値のリスト(精度判定用)
UF: list = [[0.0 for _ in range(M + 1)] for _ in range(N + 1)]
# 初期値設定
_set_initial_condition(
array_2d=U,
grid_counts_x=M,
grid_counts_y=N,
)
_set_boundary_condition(
array_2d=U,
grid_counts_x=M,
grid_counts_y=N,
grid_space=H,
)
# 計算
calc_count: int = 0
for _ in range(MK):
for j in range(1, N):
for i in range(1, M):
UF[i][j] = U[i][j] # 収束判定に必要なため、UをUFにコピー
U[i][j] = (
U[i + 1][j] + U[i - 1][j] + U[i][j + 1] + U[i][j - 1]
) / 4.0
calc_count += 1
# 収束判定
if _is_converged(U=U, UF=UF, M=M, N=N):
print("収束しました")
break
return U, calc_count
このcalculate_equation関数は、差分方程式の数値解を計算するためのものです。楕円形方程式の解を求める際に使用される一般的な手法を採用しています。関数の主要な部分とその動作について以下に説明します。
1. パラメータ
MとN: これらは格子の点の数をX軸とY軸に沿って指定します。H: 刻み幅を示します。これは、格子点間の空間的な間隔を定義します。MK: 最大の計算回数を指定します。
2. 変数の初期化
U: 解を格納する2次元配列です。初期値は全て0.0に設定されます。UF:Uと同じサイズの2次元配列で、収束判定に使用されます。
3. 初期条件と境界条件の設定
_set_initial_condition: 配列Uに初期条件を設定します。これにより、特定の問題に対する初期状態が定義されます。_set_boundary_condition: 配列Uに境界条件を設定します。これにより、問題の空間的な境界に対する挙動が定義されます。
4. 計算プロセス
- 計算は
MK回繰り返されます。各反復で、配列Uの各要素はその隣接要素の平均値に更新されます。このステップは差分方程式の離散化を表しており、ガウス-ザイデル法の一部です。 - 各反復の後、
UはUFにコピーされ、収束判定_is_convergedが行われます。もし収束条件を満たした場合、計算は終了します。
5. 収束判定
_is_converged: この関数は、古い値UFと新しい値Uの間の差を評価し、それが十分小さいかどうかを判断します。これにより、数値解が安定したかどうかが確認されます。
6. 結果の返却
- 関数は最終的に2次元配列
U(計算された解)と実際に行われた計算回数calc_countを返します。
3. 2次元配列のデータをカラープロット
def color_plot(
*,
array_2d: list,
grid_counts: int,
grid_space: float,
) -> None:
"""
2次元カラープロット
array_2dのi行j列のままimshowでプロットすると、
原点が左上、横軸が右向き、縦軸が下向きになる。
そこで、array_2dをx軸、y軸としてプロットするために、
転置してからorigin="lower"で縦軸を上向きにしてプロットする。
"""
# グラフの軸の範囲を指定
min_x_y = 0.0 - grid_space / 2
max_x_y = grid_space * grid_counts + grid_space / 2
extent=(min_x_y, max_x_y, min_x_y, max_x_y)
# 2次元配列を転置
array_2d = np.array(array_2d).T
plt.imshow(
array_2d,
cmap="viridis",
interpolation="none",
aspect="auto",
origin="lower",
extent=extent,
)
plt.colorbar()
plt.savefig("./2d_color_plot.png", format="png")
このcolor_plot関数は、2次元配列のデータをカラープロットとして可視化するためのものです。特に数値シミュレーションや数値解析で得られた結果を図示する際に用いられます。関数の主要な特徴を以下に説明します。
1. パラメータ
array_2d: 可視化するデータが含まれる2次元配列。grid_counts: グリッドの数を指定します。これは配列のX軸とY軸のサイズを示します。grid_space: グリッド間の空間的な間隔(刻み幅)。
2. グラフの軸の範囲指定
min_x_yとmax_x_y: これらはグラフのX軸とY軸の範囲を決定します。extent:imshow関数に渡されるパラメータで、画像の表示範囲を指定します。
3. 2次元配列の転置
array_2d = np.array(array_2d).T: 2次元配列を転置しています。これにより、元のデータの行と列が入れ替わり、通常の直交座標系での表示に適した形になります。
4. カラープロットの生成
plt.imshow:matplotlibのimshow関数を使用して2次元データを画像として表示します。cmap="viridis": カラーマップをviridisに設定。これは一般的なカラーマップの一つで、データの変化を色で表現します。interpolation="none": 画像の補間を行わない設定です。aspect="auto": 画像のアスペクト比を自動調整します。origin="lower": 画像の原点を下左に設定します。extent=extent: 画像の表示範囲を設定。
5. カラーバーの追加と保存
plt.colorbar(): カラーバーを追加して、データの値に対応する色のスケールを表示します。plt.savefig("./2d_color_plot.png", format="png"): グラフをPNGファイルとして保存します。
4. 結果のファイル出力
def output_result_file(
array_2d: list,
grid_counts_x: int,
grid_counts_y: int,
grid_space: float,
calc_count: int,
) -> None:
"""2次元配列をテキストファイルに書き出す"""
with open("./calculated_result.txt", "w") as file:
file.write(f"# This file shows calculated result as below.\\n\\n")
file.write(f"# Calculation Parameters.\\n")
file.write(f"grid_counts_x: {grid_counts_x}\\n")
file.write(f"grid_counts_y: {grid_counts_y}\\n")
file.write(f"grid_space: {grid_space}\\n")
file.write(f"calculation_count: {calc_count}\\n\\n")
file.write(f"# Calculated Matrix H.\\n")
for row in array_2d:
line = " ".join(map(str, row))
file.write(line + "\\n")
このoutput_result_file関数は、計算された2次元配列のデータをテキストファイルに出力するために使用されます。具体的には、数値シミュレーションや数値解析の結果を保存するのに便利です。以下に関数の動作を説明します。
1. ファイルの作成と書き込み
with open("./calculated_result.txt", "w") as file: この文は、カレントディレクトリにcalculated_result.txtという名前の新しいテキストファイルを作成し、書き込みモードで開きます。withステートメントを使用することで、ファイル操作が終了した後にファイルが自動的に閉じられることが保証されます。
2. 計算パラメータの書き込み
- 関数はまず、計算に使用されたパラメータ(
grid_counts_x,grid_counts_y,grid_space,calc_count)の情報をファイルに書き込みます。これにより、データの解析や再現に必要な情報が文書化されます。
3. 計算されたデータの書き込み
- 次に、
array_2dに格納された2次元配列(ここでは計算されたマトリックスH)の各行をテキストファイルに書き出します。 for row in array_2d: このループは、配列の各行を反復処理します。line = " ".join(map(str, row)): 各行の要素(数値)を文字列に変換し、空白で区切って1つの文字列に結合します。file.write(line + "\\\\n"): 変換された文字列をファイルに書き込み、各行の後に改行を挿入して、次の行が新しい行になるようにします。
5. その他の関数
def _set_initial_condition(
*,
array_2d: list,
grid_counts_x: int,
grid_counts_y: int,
) -> None:
"""
初期条件の設定
境界以外のU値を全て0.0001とおく
"""
for j in range(1, grid_counts_y):
for i in range(1, grid_counts_x):
array_2d[i][j] = 0.0001
def _set_boundary_condition(
*,
array_2d: list,
grid_counts_x: int,
grid_counts_y: int,
grid_space: float,
) -> None:
"""境界条件の設定"""
# y=0上の境界条件
for i in range(grid_counts_x + 1):
array_2d[i][0] = 0.0
# y=M上の境界条件
for i in range(grid_counts_x + 1):
array_2d[i][grid_counts_y] = (
4 * (grid_space * i) * (1.0 - grid_space * i)
)
def _is_converged(*, U: list, UF: list, M: int, N: int) -> bool:
"""
収束判定を行う
誤差の合計の相対量がERROR_CONSTANT以下になったら収束と判定する
"""
ERROR_CONSTANT: float = 0.0001 # 精度定数
sum: float = 0.0 # 誤差の初期値
sum0: float = 0.0
for j in range(1, N):
for i in range(1, M):
sum0 += abs(U[i][j])
sum += abs(U[i][j] - UF[i][j])
sum = sum / sum0
return sum <= ERROR_CONSTANT
このコードの断片は、数値解析、特に偏微分方程式の解法において、初期条件と境界条件の設定、および収束判定のための関数を定義しています。これらの関数は数値解析のプロセスにおいて重要な役割を果たします。
_set_initial_condition関数
目的
- 2次元配列(一般的には数値解析で使用される格子点のマトリックス)に初期条件を設定します。
動作
array_2d: 解析で使用される2次元配列。grid_counts_xとgrid_counts_y: X軸とY軸に沿った格子点の数。- 配列の各要素(境界を除く)に値
0.0001を設定します。
_set_boundary_condition関数
目的
- 2次元配列の境界に特定の条件を設定します。
動作
y=0の境界(最下行)には、すべての値を0.0に設定。y=Mの境界(最上行)には、計算式4 * (grid_space * i) * (1.0 - grid_space * i)に基づいて値を設定。ここで、grid_spaceは格子点間の間隔を示します。
_is_converged関数
目的
- 数値解法が収束したかどうかを判定します。
動作
U: 現在の計算ステップでの配列。UF: 前の計算ステップでの配列。MとN: X軸とY軸に沿った格子点の数。UとUFの各要素の差を計算し、その絶対値の和を取ります。- この和が全体の差の和
sum0に対して十分に小さい(ERROR_CONSTANT以下)場合、収束したと判断します。
最後に
有限差分法を用いた偏微分方程式の数値解法についてご紹介しました。
Pythonで書いた計算プログラムも惜しみなく公開していますので、ぜひ動かしながら理解を深めてください。
今後は楕円方程式以外の偏微分方程式についても数値的に解けるように、新たな記事を執筆していきますので、そちらもご覧いただけたら幸いです。
Pythonで学ぶ偏微分方程式の数値シミュレーションの技術書を販売中
¥2,500 → ¥1,000 今なら60%OFF!!
計算方法、グラフやアニメーションの作成方法、計算ログの残し方を惜しみなく解説しています!
理論と実装の溝を埋めてくれる良書です!




