【Gaussian】一点計算を用いた分子の電子密度とエネルギー解析実践

【Gaussian】一点計算を用いた分子の電子密度とエネルギー解析実践

SHARE

この記事では、Gaussianソフトウェアを使用した一点計算（Single Point Calculation）の実践方法とその応用について解説します! Gaussianを用いた一点計算の基本から始め、具体的な計算手順、そしてエネルギーと電子密度計算のoutputファイルの確認方法までを網羅しています。この記事を身につけることで、分子の電子的性質や反応性に関する理解を得られるようになります。

動作検証済み環境

Windows 11(22H2), Gaussian16、Avogadro 1.2.0
【初心者向け】Gaussianを使った量子化学計算入門

Gaussianを使った量子化学計算の初心者向け技術書を販売中

¥2,000 → ¥1,000 今なら50%OFF!!

しばしば出くわすエラーへの対処法をはじめ
Gaussianと無料ソフトウェア Avogadro を組み合わせた物性解析手法が学べます！

技術書ページへ

1. 一点計算とは

一点計算の重要性と応用分野

一点計算は、特定の分子や材料のエネルギーや他の特性を出すための計算手法です。この方法を使って、分子がどれだけ安定かや、化学反応でどう変化するかなどを調べることができます。新しい薬を開発する時や、新しい材料を作る時に、どんな性質を持つかを予測するのに役立ちます。つまり、分子設計、材料科学、薬剤開発などの多くの分野で、事前に物質の振る舞いを知るために重要なツールです。

一点計算と構造最適化の違いと注意点

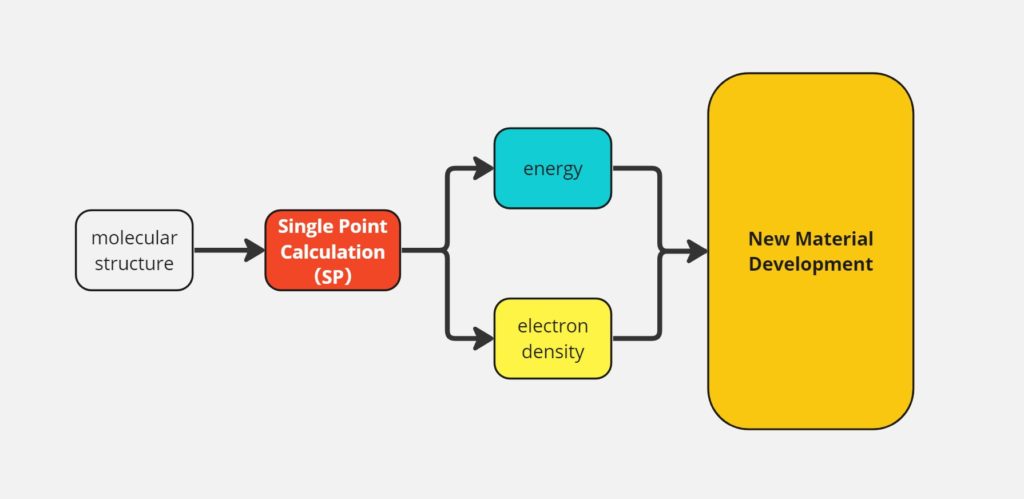
一点計算と構造最適化は、量子化学計算の二つの主要な手法ですが、目的とするところが異なります。

  • 一点計算は、既知の分子や材料の形（三次元構造）を基に、その性質（エネルギーや電子密度など）を計算する方法です。既に分子の構造が分かっている時に使います。
  • 構造最適化は、分子や材料がどのような形をすれば最も安定するかを見つけるプロセスです。分子内の原子の位置を動かしながら、エネルギーが最も低くなる形を探します。

注意点

  • 一点計算をする前には、対象の分子の構造が正確であることが大切です。これは、実験データや他の計算方法で得られた構造情報に基づいて設計します。
  • 構造最適化は必須です。一点計算の前にこのステップを行うことで、計算結果の正確性を高めることができます。未最適化の構造では、誤った結果になる可能性があります。一方で、構造最適化により目的の構造が崩れてしまう場合はこの限りではありません（タンパク質のフラグメント計算など）。
  • 計算リソースを考える必要があります。構造最適化は時間と計算能力を多く消費する一方で、一点計算は比較的少ないコストで計算できます。

簡単に言うと、一点計算は「既に分かっている形の性質を計算する」ため、構造最適化は「最も安定する形を見つける」ための計算です。

一点計算で求められる物性値

一点計算を通じて求められる物性値には、以下のようなものがあります。

  • エネルギー: 分子の安定性や反応性を理解するために最も直接的な指標となります。
  • 分子軌道のエネルギー: 電子の分布や化学反応における電子の移動を理解するために重要です。
  • 電荷分布: 分子内の電荷の偏りを理解することで、分子間相互作用や反応性の予測に役立ちます。
  • 双極子モーメント: 分子の極性を表し、溶解性や分子間相互作用の強さに影響します。

2. 一点計算の実践

一点計算を実行し、成功させるための主要なステップを説明します。

一点計算の準備

  • 構造の選定: 一点計算の対象となる分子や材料の三次元構造を定めます。この構造は、実験的に得られたデータ（例えば、X線結晶構造解析）や、他の計算手法によって最適化されたもの（例えば、分子動力学シミュレーション）から取得することが一般的です。 今回はカフェイン分子を対象に実践します。
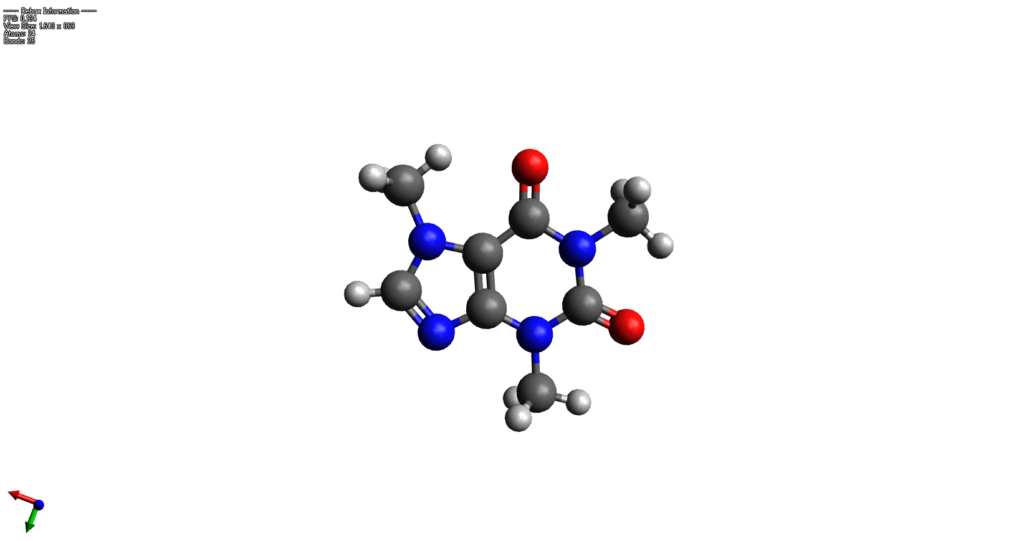
  • 計算レベルの選択: 目的に応じて、適切な計算手法（Hartree-Fock法、密度汎関数理論（DFT）、ポストハートリー・フォック法など）と基底関数セットを選択します。構造最適化と異なり、一点計算では比較的計算コストが小さいため、高い計算レベルで計算することも可能です。

具体的な計算手順

1. 入力ファイルの構成

計算に必要な情報（分子の構造、計算手法、基底関数セットなど）を含む入力ファイルを作成します。以下はカフェイン分子を一点計算する際のInputファイルです。

%Chk = C:\User\Desktop\caffeine.chk
#p B3LYP/3-21G SP output=wfn pop=npa scf=xqc

 Title

0 1
C          0.53311        3.03017       -0.00246
C          1.72670        2.31091       -0.00208
C          1.70454        0.95269       -0.00259
C         -0.65041        0.92795       -0.00387
N         -0.66124        2.32431       -0.00337
N          0.55236        0.23197       -0.00348
N          3.01587        2.71469       -0.00124
N          2.95819        0.46071       -0.00209
C          3.73818        1.56829       -0.00126
C          3.59160        4.05859       -0.00044
H          2.81931        4.84825       -0.00057
H          4.22349        4.19098       -0.90372
H          4.22251        4.19032        0.90362
C         -1.92838        3.07568       -0.00378
H         -2.81987        2.41488       -0.00450
H         -1.98337        3.71796       -0.90855
H         -1.98435        3.71729        0.90140
C          0.61671       -1.23616       -0.00398
H         -0.38992       -1.70349       -0.00470
H          1.15621       -1.58820        0.90106
H          1.15720       -1.58754       -0.90869
O          0.53510        4.24945       -0.00202
O         -1.70466        0.31136       -0.00467
H          4.82025        1.53546       -0.00069

C:\User\Desktop\caffeine.wfn
  • %Chk = C:\\User\\Desktop\\caffeine.chk この行は、計算の結果を保存するチェックポイントファイル（caffeine.chk）のパスを指定しています。チェックポイントファイルには、計算過程のデータが保存され、後で分析や追加計算に使用できます。
  • #p B3LYP/3-21G SP output=wfn pop=npa scf=xqc ここでは、計算のタイプとパラメータを指定しています。
    • B3LYP/3-21Gは、使用する理論レベルと基底関数セットです。B3LYPは汎用的な密度汎関数理論(DFT)の汎関数で、3-21Gは比較的単純な基底関数セットです。
    • SPは一点計算（Single Point）を意味します。
    • output=wfnは、計算の結果をウェーブファンクションファイル（caffeine.wfn）に出力することを指示しています。ウェーブファンクションファイルは物性解析をソフトウェアで行う時に使用する為、出力しておくと便利です。
    • pop=npaは、自然密度解析（Natural Population Analysis）を行うことを指示しています。ここから算出される自然電荷はMulliken電荷に比べ基底関数依存性が小さく、直観的に説得力のある数値を与えることが多いのが特徴です。
    • scf=xqcは、SCF（Self-Consistent Field）計算に特定の収束基準を使用することを指示しています。この設定は必須ではありませんが、使用しない場合L9999エラー等が出る場合があります。
  • Title ここでは、計算のタイトルや説明を記載します。
  • 0 1 この行は、分子の電荷（0）とスピン多重度（1）を示しています。多重度はスピン状態を表し、ここではシングレット状態（スピン対成）を意味します。
  • 次の部分では、カフェイン分子の原子の種類と3次元座標（x, y, z）が列挙されています。例えば、C 0.53311 3.03017 -0.00246は、炭素原子が（0.53311, 3.03017, -0.00246）の位置にあることを示しています。
  • C:\\User\\Desktop\\caffeine.wfn 計算結果が出力されるウェーブファンクションファイルのパスを指定しています。
  • 空白行 3, 5, 31, 33, 34行目にある空白行はプログラム上、意味のある空白です。特に最後2行の空白（33, 34行目）は忘れやすいので注意しましょう。

2. 計算の実行

計算化学ソフトウェアGaussianを使用して、入力ファイルに基づいて一点計算を実行します。

GaussianをWindows、Linux、およびmacOSで実行する方法を整理しておきます。それぞれのシステムでの基本的な実行方法が異なるため、環境ごとの指示に従う必要があります。

  • Windowsでの実行方法

Windows環境でGaussianを実行する際には、GUIベースの方法が一般的ですが、コマンドライン（コマンドプロンプトやPowerShell）を使って実行することも可能です。

GUIを使用した実行:

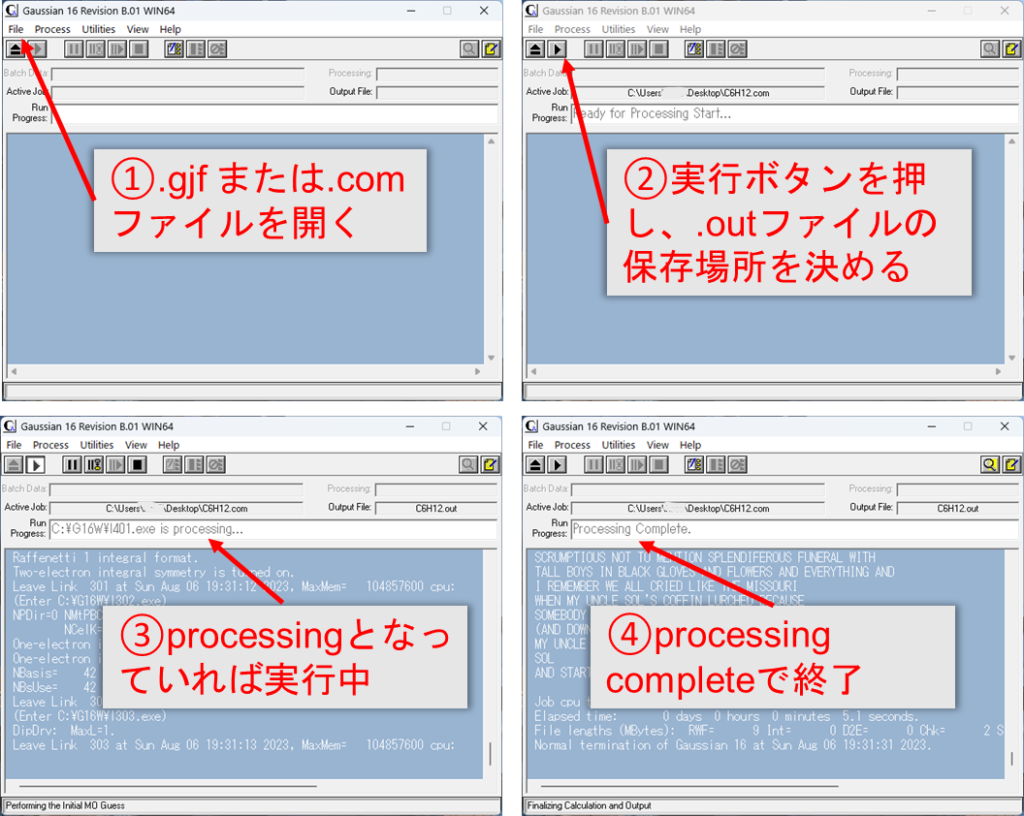
  1. Gaussianを開きます。
  2. File > Open を選択して、入力ファイル（.gjfまたは.comファイル）を開きます。
  3. 計算を設定し、▶をクリックして計算を実行します。
  4. 出力ファイル（通常は.logまたは.outファイル）を指定した場所に保存します。

コマンドラインを使用した実行:

コマンドプロンプトやPowerShellで以下のコマンドを使用します。

g16 inputfile.gjf

g16 は Gaussian 16の実行コマンドです。使用しているバージョンに応じて g09 などに変更してください。

inputfile.gjf は Gaussianの入力ファイル名です。

  • LinuxおよびmacOSでの実行方法

LinuxとmacOSでは、ターミナルからコマンドラインを使用してGaussianを実行します。

g16 inputfile.gjf

g16 は Gaussian 16の実行コマンドです。使用しているバージョンに応じて g09 などに変更してください。

inputfile.gjf は Gaussianの入力ファイル名です。

計算サーバーやワークステーションでの実行（Unix/Linux環境）:

  1. 入力ファイル（.gjf または .com ファイル）を計算サーバーの適切なディレクトリにアップロードします。
  2. ターミナルまたはSSHクライアント（例: PuTTY , WinSCP）を使用してサーバーに接続します。
  3. ジョブを実行するコマンドを入力します。 特定の計算機リソースでカスタマイズされたジョブサブミッションスクリプトを使用する場合があります。 g16sub inputfile.gjf

注意点

  • コマンドを実行する前に、Gaussianが正しくインストールされ、環境変数が適切に設定されていることを確認してください。
  • パスが正しく設定されていない場合や、権限に関する問題がある場合は、エラーが発生することがあります。その場合は、システム管理者に相談するか、インストールドキュメントを再確認してください。
  • macOSで g09 や g16 コマンドがうまく機能しない場合は、Gaussianのインストールディレクトリにパスを設定するか、フルパスでコマンドを実行してみてください。

3. 計算終了の確認

計算が終了したら、outputファイルを開き最後の行を見てください。以下のようなコメントがあれば終了です。

Job cpu time:       0 days  0 hours  4 minutes 59.0 seconds.
Elapsed time:       0 days  0 hours  4 minutes 57.7 seconds.
File lengths (MBytes):  RWF=     15 Int=      0 D2E=      0 Chk=      3 Scr=      1
Normal termination of Gaussian 16 at Thu Mar 07 22:01:15 2024.

計算結果の解析と評価

計算が完了したら、出力ファイルから重要な結果（エネルギー、電子密度、分子軌道エネルギーなど）を抽出します。

エネルギーの確認方法

エネルギーの確認は、計算が終了して出てくるoutputファイル（.out）をテキストエディタ等で開き、SCF Doneを文字列を検索することで確認できます。windowsであればcontrol + F キーを押すことで検索窓が出てきます。検索すると以下のような結果が出てきます。

 SCF Done:  E(RB3LYP) =  -676.628498076     A.U. after   15 cycles
            NFock= 15  Conv=0.63D-08     -V/T= 2.0085
 KE= 6.709555985320D+02 PE=-3.422811531950D+03 EE= 1.151917515089D+03

SCF Doneというメッセージは、Gaussian出力ファイル内で、自己無撞着場（Self-Consistent Field, SCF）計算が完了したことを示しています。このメッセージに続く情報は、計算が成功し、エネルギーが収束したことを意味し、計算された分子の電子エネルギーとその他の関連情報を提供します。ここでの各項目を解説します：

  • E(RB3LYP) = -676.628498076 A.U. これは、計算された分子の電子エネルギーです。ここでは、RB3LYPという密度汎関数理論（Density Functional Theory, DFT）を用いた計算で、エネルギー単位は原子単位系（Hartree, A.U.）で表示されています。この値は、分子の安定性や化学反応のエネルギー解析に使用されます。
  • after 15 cycles SCF計算が収束するまでに要した反復回数です。このケースでは、15回の反復計算後に収束しました。
  • NFock= 15 Fock行列が計算された回数を示しています。この数値も反復計算の回数と一致しています。
  • Conv=0.63D-08 収束基準です。この値は、SCF計算の収束基準（通常は電子密度の変化やエネルギーの変化）を満たしたことを示しており、ここでは約6.3×10^-9 A.U.の精度で収束しています。
  • V/T= 2.0085 ポテンシャルエネルギーと運動エネルギーの比率を示しています。この比率は、系の電子構造の特性を反映しています。
  • KE= 6.709555985320D+02 分子の運動エネルギー（Kinetic Energy, KE）です。単位はHartree（A.U.）です。
  • PE=-3.422811531950D+03 分子のポテンシャルエネルギー（Potential Energy, PE）です。こちらもHartree（A.U.）で表示されています。
  • EE= 1.151917515089D+03 分子の電子エネルギー（Electronic Energy, EE）です。これもHartree（A.U.）の単位を用いています。

これらの情報を総合することで、計算された分子のエネルギー的特性を理解することができ、これらは化学反応の可否、反応経路、分子間相互作用の分析など、様々な化学的問題の解決に役立ちます。

電子密度の解析（Natural Population Analysis）の確認方法

分子軌道と電子密度の解析（Natural Population Analysis）の確認は、計算が終了して出てくるoutputファイル（.out）をテキストエディタ等で開き、 Summary of Natural Population Analysisを文字列を検索することで確認できます。

                                   Natural Population
            Natural  -----------------------------------------------
Atom  No    Charge         Core      Valence    Rydberg      Total
  C    1    0.59232      1.99885     3.37353    0.03530     5.40768
  C    2   -0.02279      1.99841     4.01320    0.01117     6.02279
  C    3    0.34989      1.99862     3.63101    0.02047     5.65011
  C    4    0.78479      1.99943     3.17977    0.03602     5.21521
  N    5   -0.50312      1.99899     5.50036    0.00377     7.50312
  N    6   -0.46227      1.99881     5.45857    0.00489     7.46227
  N    7   -0.36995      1.99891     5.36549    0.00555     7.36995
  N    8   -0.49568      1.99913     5.49101    0.00554     7.49568
  C    9    0.19677      1.99919     3.78394    0.02009     5.80323
  C   10   -0.48220      1.99885     4.47782    0.00553     6.48220
  H   11    0.27059      0.00000     0.72330    0.00611     0.72941
  H   12    0.23977      0.00000     0.75928    0.00095     0.76023
  H   13    0.23977      0.00000     0.75928    0.00095     0.76023
  C   14   -0.47477      1.99887     4.46861    0.00729     6.47477
  H   15    0.25721      0.00000     0.73888    0.00390     0.74279
  H   16    0.23999      0.00000     0.75834    0.00167     0.76001
  H   17    0.23999      0.00000     0.75834    0.00167     0.76001
  C   18   -0.46911      1.99887     4.46423    0.00601     6.46911
  H   19    0.25917      0.00000     0.73699    0.00384     0.74083
  H   20    0.24101      0.00000     0.75767    0.00132     0.75899
  H   21    0.24101      0.00000     0.75767    0.00132     0.75899
  O   22   -0.54350      1.99964     6.54238    0.00147     8.54350
  O   23   -0.56553      1.99964     6.56458    0.00132     8.56553
  H   24    0.23664      0.00000     0.76260    0.00076     0.76336
  =======================================================================
　 * Total * 0.00000 　　27.98621 　　73.82686 　0.18692 　　102.00000
  • Natural Charge: 原子に割り当てられた実質的な電荷です。この値は、理想的な中性状態（原子核の電荷に等しい電子の数）からの偏差を示します。正の値は電子が不足していることを示し、負の値は電子が過剰に存在することを意味します。
  • Core: 原子核に非常に近い領域に存在する、非常に強く束縛された電子の数です。
  • Valence: 原子の価電子の数です。これは化学反応において最も関与しやすい電子で、分子の結合形成に直接関与します。
  • Rydberg: 高エネルギー状態の電子、または価電子層より外側に存在する電子の数です。これらは通常、化学反応には直接関与しませんが、分子の光物理的特性に影響を与えることがあります。
  • Total: 原子上の電子の総数です。

解析例

  • 炭素原子（C）1は自然電荷が+0.59232で、これは炭素が電子を若干失っていることを意味します。
  • 酸素原子（O）22は自然電荷が-0.54350で、これは酸素が余分な電子を持っていることを示しています。

電子構成

その下の「Natural Electron Configuration」セクションでは、各原子の電子構成が示されます。例えば、炭素原子1は [core]2S(0.77)2p(2.61)3p(0.03) とあります。これは、コア電子以外に2s軌道に0.77個、2p軌道に2.61個、3p軌道に0.03個の電子が存在することを示しています。

   Atom  No          Natural Electron Configuration
 ----------------------------------------------------------------------------
      C    1      [core]2S( 0.77)2p( 2.61)3p( 0.03)
      C    2      [core]2S( 0.82)2p( 3.19)3p( 0.01)
      C    3      [core]2S( 0.77)2p( 2.86)3p( 0.02)
      C    4      [core]2S( 0.73)2p( 2.45)3p( 0.03)
      N    5      [core]2S( 1.24)2p( 4.26)
      N    6      [core]2S( 1.19)2p( 4.26)
      N    7      [core]2S( 1.20)2p( 4.17)3p( 0.01)
      N    8      [core]2S( 1.42)2p( 4.07)3p( 0.01)
      C    9      [core]2S( 0.92)2p( 2.86)3p( 0.02)
      C   10      [core]2S( 1.11)2p( 3.37)
      H   11            1S( 0.72)2S( 0.01)
      H   12            1S( 0.76)
      H   13            1S( 0.76)
      C   14      [core]2S( 1.10)2p( 3.37)3p( 0.01)
      H   15            1S( 0.74)
      H   16            1S( 0.76)
      H   17            1S( 0.76)
      C   18      [core]2S( 1.10)2p( 3.36)3p( 0.01)
      H   19            1S( 0.74)
      H   20            1S( 0.76)
      H   21            1S( 0.76)
      O   22      [core]2S( 1.72)2p( 4.83)
      O   23      [core]2S( 1.72)2p( 4.85)
      H   24            1S( 0.76)

NPAによる解析は、分子の電荷分布を理解し、どの原子が電子を受け取りやすいか、またはどの原子が電子を失いやすいかを知るのに役立ちます。これにより、分子の化学的性質や反応性についての洞察を得ることができます。

描写ソフトウェアによる評価

分子構造のモデリング、可視化、および解析を行う上で、GaussViewやAvogadroのような描写ソフトウェアを活用することは、計算結果をより直観的に理解するための重要な選択肢の一つです。これらのグラフィカルインターフェースソフトウェアは、分子の3次元構造を直感的に捉えることができるだけでなく、様々な計算化学のシミュレーションを設定し、解析することが可能です。これにより、複雑な計算結果も理解しやすくなり、分子の性質や反応機構に関する深い洞察を得ることができます。

Avogadroはこちらの記事で解説していますので興味があれば是非読んでみてください。

3. 一点計算の応用例

一点計算は、分子や材料の理論的研究において幅広く応用されます。ここでは、一点計算の主な応用例について説明します。

分子のエネルギー計算

分子のエネルギー計算は、一点計算の最も基本的な応用の一つです。この計算を通じて、分子の安定性や反応性を評価することができます。分子の全エネルギーを計算することで、異なる分子構造間の相対的な安定性を比較したり、最もエネルギーが低い、すなわち最も安定した構造を特定することが可能になります。この情報は、新しい化合物の設計や既知の化合物の性質を理解するために重要です。

使用例：MDシュミレーションなど力場による計算によって得られた高分子の構造のエネルギー計算

反応の活性化エネルギー計算

化学反応が進行するために必要なエネルギー、すなわち活性化エネルギーの計算も一点計算の重要な応用です。活性化エネルギーを計算することで、反応の速度やその反応がどれだけ進みやすいかを理論的に評価することができます。これは、触媒の設計や反応機構の解析において非常に役立ちます。反応経路上の遷移状態（最も高いエネルギーを持つ状態）のエネルギーを計算することで、反応の活性化エネルギーを特定することが可能です。

使用例：低い計算レベルで得られた反応経路上の遷移状態を高い計算レベルで再計算

分子軌道と電子密度の解析

分子軌道のエネルギーと電子密度の分布を計算することにより、分子内の電子の振る舞いや化学結合の性質を詳細に理解することができます。分子軌道の解析により、結合形成や解離に関与する電子の位置を特定したり、化学反応における電子移動のメカニズムを解明することができます。また、電子密度の分布を分析することで、分子内の電荷分布や分極性、さらには非共有電子対の位置などを明らかにすることが可能です。これらの情報は、分子間相互作用の理解や、分子の光学的、電気的性質の予測に不可欠です。

使用例：実験的に決定された構造データ（単結晶構造解析によって得られた錯体分子構造）の電荷分布や分極性の調査

5. よくある質問

計算化学のシミュレーション、特に量子化学計算を行う際、計算が収束しない場合や計算精度を高めたい場合があります。以下では、これらの状況に対処するための一般的なアプローチについて解説します。

計算が収束しない場合の対処法

計算が収束しない場合、以下の点を検討することが役立ちます。

  1. 入力ファイルの確認: まず収束せずエラーが出る場合の多くが入力ファイルの設定ミスです。計算を実行する前に以下のチェックリストを確認しましょう。 エラーを少なくするための入力ファイル最終チェックリスト
    • [ ] 入力ファイルの最後に空行はあるか？
    • [ ] 各セクションの区切り空行は入っているか？
    • [ ] 全角文字が入っていないか
    • [ ] 使用するメモリ量・プロセッサ数は適切か
    • [ ] Gaussianキーワードは正しいスペルか？（汎関数や基底関数、オプションなど）
    • [ ] チェックポイントファイル（.chk）の名前に特殊文字（[,][.][[\][:][¥]など）が入っていないか
    • [ ] 電荷とスピン多重度は正確か？
    • [ ] 分子構造指定は適切か？
  2. 初期構造の最適化: 分子の初期構造が実際の最小エネルギー構造から遠い場合、収束に時間がかかるか、まったく収束しないことがあります。より現実に近い初期構造から計算を開始すると、収束しやすくなることがあります。
  3. 基底関数セットの選択: 基底関数セットが小さすぎると、計算が不正確になる可能性があります。適切なサイズの基底関数セットを選択することが重要ですが、大きすぎると計算コストが大幅に増加します。時には、異なるタイプの基底関数セットを試すことも収束問題の解決に役立ちます。

計算精度を高める方法

計算精度を向上させるためには、以下のアプローチが考えられます。

  1. 基底関数セットの拡張: 基底関数セットを拡張することで、計算の精度を高めることができます。例えば、ポーラライゼーション関数や拡散関数を含む基底関数セットを使用すると、より精度の高い結果が得られます。
  2. ポストHF法の使用: ハートリー・フォック法よりも高度な計算方法（例：密度汎関数理論（DFT）、摂動理論（MP2）、結合クラスター法（CCSD(T)）など）を使用することで、相関エネルギーを考慮し、より正確な結果を得ることができます。
  3. 収束基準の厳格化: 計算の収束基準をより厳格に設定することで、計算の精度を向上させることが可能です。しかし、これには計算コストが増加する可能性があるため、バランスを取ることが重要です。
  4. ゼロポイントエネルギーや熱力学的補正の考慮: 可能であれば、ゼロポイントエネルギーの補正や温度、圧力に関する熱力学的補正を計算に含めることで、実験値により近い結果を得ることができます。

これらのアプローチを通じて、計算化学のシミュレーションにおける収束問題の解決や計算精度の向上が期待できます。それぞれの計算に最適な設定は異なるため、実際にいくつかの異なる方法を試しながら最良の結果を得るための条件を見つけることが重要です。

最後に

いかがでしたでしょうか？一点計算は比較的大きな分子も計算でき、エネルギーや分子軌道、電荷分布の情報を得ることが出来るため、非常に幅広い分野で活用できます。是非これを機に挑戦してみてください。

参考文献

[1] 西長亨、本田康 「有機化学者のための量子化学計算入門 Gaussianの基本と有効利用のヒント」　第7章　P. 106-108

[2] Avogadro 公式 https://avogadro.cc/　(参照2024-3-7)

[3] Gaussian 16, Rev. A.03, Gaussian, Inc., Wallingford CT, 2016.

【初心者向け】Gaussianを使った量子化学計算入門

Gaussianを使った量子化学計算の初心者向け技術書を販売中

¥2,000 → ¥1,000 今なら50%OFF!!

しばしば出くわすエラーへの対処法をはじめ
Gaussianと無料ソフトウェア Avogadro を組み合わせた物性解析手法が学べます！

技術書ページへ

コメントを残す

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です

前の記事

ToxicophoresとQSAR
【AI創薬】【毒性予測】 Toxicophores、QSARを…

次の記事

【ImageJ】画像内のスケールを利用したサイズの計測【画像解…