短時間フーリエ変換 (STFT) を用いて時間周波数解析を行う場合,解析したい信号の時間変化に対して窓関数幅を適切に選択する必要がありました。
しかしながら,窓関数幅の選択は試行錯誤が伴い,手間がかかる場合があります。
これを解決する一つの方策がウェーブレット解析です。
この記事ではウェーブレット変換を用いた時間周波数解析,スカログラムの表示方法について紹介します。
なお,本記事は C. Torrence and G. P. Compo (1998) の論文に大きく依拠しています。
macOS Big Sur, python3.7.9

ウェーブレット変換とは?フーリエ変換との違いは?
ウェーブレット変換とは、信号や画像データを解析するための数学的手法の1つで、時間と周波数の両方の情報を得ることができます。ウェーブレット関数と呼ばれる短い波形を用いて、データを異なるスケール(解像度)と位置で表現することが特徴です。
一方、フーリエ変換は、信号を周波数成分に分解し、それらの振幅と位相を求めることができる数学的手法です。フーリエ変換は、信号を正弦波や余弦波の無限和で表現することができますが、時間情報は失われることが欠点です。
ウェーブレット変換とフーリエ変換の違いを簡潔にまとめると、ウェーブレット変換は時間と周波数の両方の情報を得られるのに対し、フーリエ変換は周波数情報のみを得ることができます。
ウェーブレット変換は信号の局所的な特徴を捉えるのに優れているため、信号の瞬間的な変化を解析する場合に適しています。
連続ウェーブレット変換
連続ウェーブレット変換
ウェーブレット $\psi$ に関する,信号 $x(t)$ の連続ウェーブレット変換 (continuous wavelet transform: CWT) は,
$$
\mathcal{W}_\psi[x](s, \tau) := \int_{-\infty}^{\infty} x(t)\psi^*\left(\frac{\tau – t}{s}\right)\mathrm{d}t
$$
と定義されます。
$s$ はスケールというパラメータで周期 (したがって,その逆数の周波数) と関連します。$\tau$ はシフトというパラメータで,時刻に対応します。
フーリエ変換のときと同じように,$|\mathcal{W}_\psi[x](s, \tau)|$ は時刻 $t = \tau$のときのスケール $s$ を持つ成分の振幅であると解釈することができます。
時刻 $t = 0$ 付近に局在するスケールの異なるウェーブレット (接尾辞レット (let) は「小さいもの」を表すもの (例えば book (本) に対する booklet (小冊子)) で,波の小破片みたいなニュアンスがあると考えられます) をずらしながら掛けて積分することによって,ウェーブレットに近いものがもとの信号にある場合にはウェーブレットの値として0でないものが出てくるということになります。
ウェーブレット $\psi$ は,窓関数×正弦波というような形をしているものを用います。スケールを変更することは,周波数を変えると同時に窓関数幅を変えていることになります。
すなわち,振動数の高いものに対しては,窓関数の幅を小さくし,振動数の小さいものに対しては,窓関数の幅を大きくするという操作が自動的に行われていることになります。
STFTのスペクトログラムに対応して,横軸に時間,縦軸に周波数 (スケール) をとって表示したものをスカログラム (scalogram) といいます。
連続ウェーブレット変換の離散化
上で定義した連続ウェーブレット変換を離散的に行います。
ウェーブレットのもとになるマザーウェーブレット (mother wavelet) と呼ばれる時間の関数 $\psi_0$ を用意しておいて,
$$
W_n(s) = \sum_{n’=0}^{N-1} x_n\psi_0^*\left(\frac{(n’-n)\Delta t}{s}\right)
$$
連続ウェーブレット変換の近似計算 (離散化) を計算するためには,すべてのスケールについて $N$ 回の畳込み計算を行う必要があります。
この場合,入力信号長が長くなってしまうと計算時間が非常長くなってしまいます。
これを回避するために,畳み込み定理を使います。畳み込み定理とは,時間空間での畳み込みの計算は周波数空間での掛け算になるというものです。
畳み込み定理を利用した方法は周波数空間への変換が必要になり一手間かかるように思えますが,これにFFTアルゴリズムを使うと非常に効率よく計算でき,トータルでみると計算量を大幅に節約できます。
マザーウェーブレット
よく使用されるマザーウェーブレットとしては,Morletのウェーブレットがあります。
Morletはウェーブレット解析を考案したフランスの技術士で日本語では「モルレー」や「モレー」と表記されることが多いです。
$$
\psi_\mathrm{M}(t) = \pi^{-1/4}e^{i\omega_0t}e^{-t^2/2}
$$
と定義され,
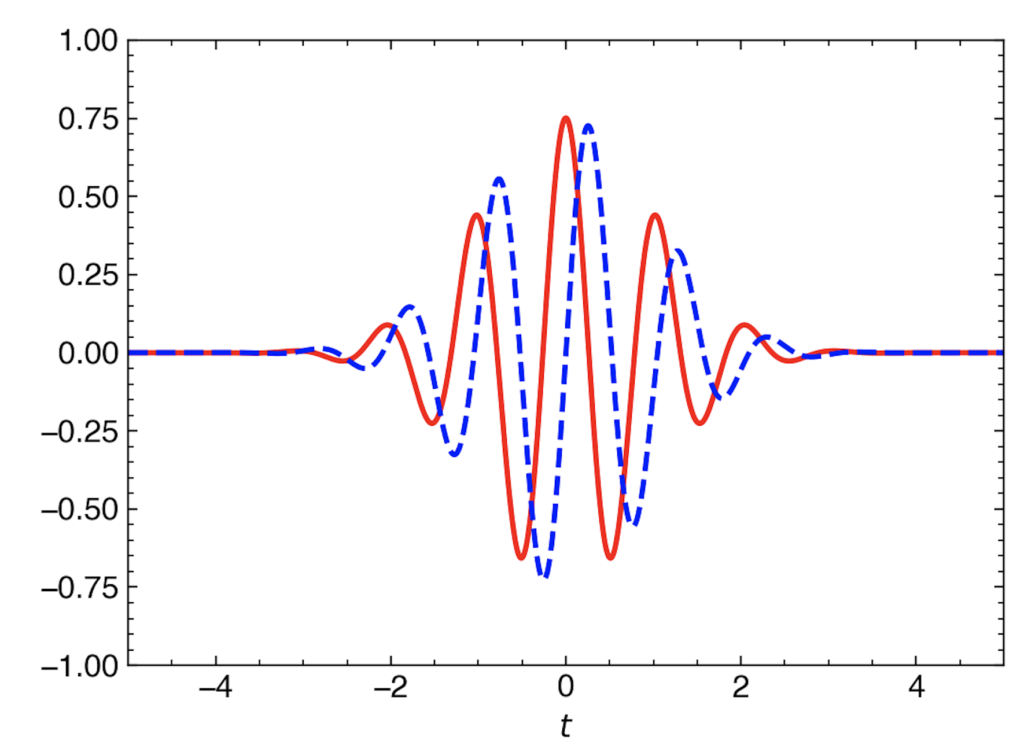
という形の関数です。赤の実線は実部,青の破線は虚部を表しています。
後で必要になるスケール $s$ のMorletのウェーブレットのフーリエ変換は (許容性の条件を満たすように修正した) スケール$s$のMorletのウェーブレット$\psi_\text{M}(t/s)$の周波数空間での表現は
$$
\Psi_\mathrm{M}(s\omega) = \pi^{-1/4} H(\omega)e^{-(s\omega – \omega_0)^2/2}
$$
です。$H(\omega)$はヘヴィサイド (Heaviside) の階段関数です。 (これはマザーウェーブレットの単純なフーリエ変換とは異なります。詳しくは記事の最後,(2023/05/16追記)の部分を参照してください。)
マザーウェーブレットとして用いられる関数は他にもあります。詳しくは C. Torrence and G. P. Compo (1998) の論文を参照してください。
スケールと周波数の対応
ウェーブレット解析においては,周波数に対応するスケール (scale) という概念が出てきます。これは,マザーウェーブレットをどれくらい時間軸方向に伸縮させるかというパラメータです。
マザーウェーブレットとしてMorletのウェーブレットを使用するとき,スケール $s$ と (疑似) 周波数 $f$ の対応関係は,
$$
f = \frac{\omega_0 + \sqrt{2 + \omega_0^2}}{4\pi s}
$$
となります。$\omega_0 = 6$ のとき,$f \simeq 0.968 s^{-1}$ となります。
スケールの離散化
スケールを離散化する必要があります。次のように離散化されることが多いようです:
$$
s_j = s_0\cdot 2^{j\Delta j}, \quad j = 0, 1, \dots, J , \\ J = \frac{1}{\Delta j}\log_2\left(\frac{N\Delta t}{s_0}\right)
$$
ここで,$s_0$ は解像可能な最小のスケール (ナイキスト周波数に対応するもの) で,フーリエ変換したときとの対応から,$s_0 = 2\Delta t$ とします。
$J$ は最も大きなスケールに対応するものです。
$\Delta j$ は周波数の解像度 (分割数) を決めるパラメータです。
スケール方向に十分な解像度が得られるように小さくする必要があります。
Cone of Interference (COI)
Cone of Interference は計算されたスカログラムの信頼性の低い領域を示すものです。
ウェーブレットがエッジの影響を受けてしまう場合は,その時間帯のスカログラムは信憑性が低いと考えられます。
モルレーのウェーブレットを使った場合,スケール $s$ のとき,エッジから $\sqrt{2}s$ だけ離れるとエッジの影響がないとされます。($\sqrt{2}s$ はウェーブレットの包絡線が $e^{-2}$ 程度減少する時間)。
スカログラムを作成する方法
上で説明したものをpythonでコーディングすると以下のようになります。
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.patheffects as path_effects
import numpy as np
#------------------------------------------------------------------------------
# テスト信号の生成
#------------------------------------------------------------------------------
dt = 1.0e-4
tms = 0.0
tme = 2.0
tm = np.arange(tms, tme, dt)
amp = abs(np.sin(2.0*np.pi*2.0*tm)) + np.tanh(tm)
freq = 10.0 + 10.0*tm*tm + np.cos(2.0*np.pi*3.0*tm)
sig = amp*np.sin(2.0*np.pi*freq*tm) + amp*5.0e-2*np.random.randn(len(tm))
#------------------------------------------------------------------------------
# 諸々の設定
freq_upper = 300.0 # in kHz
out_fig_path = "scalogram.png"
#------------------------------------------------------------------------------
# 連続ウェーブレット変換
# --- n_cwt をlen(sig)よりも大きな2のべき乗の数になるように設定
n_cwt = int(2**(np.ceil(np.log2(len(sig)))))
# --- 後で使うパラメータを定義
dj = 0.125
omega0 = 6.0
s0 = 2.0*dt
J = int(np.log2(n_cwt*dt/s0)/dj)
# --- スケール
s = s0*2.0**(dj*np.arange(0, J+1, 1))
# --- n_cwt個のデータになるようにゼロパディングをして,DC成分を除く
x = np.zeros(n_cwt)
x[0:len(sig)] = sig[0:len(sig)] - np.mean(sig)
# --- omega array
omega = 2.0*np.pi*np.fft.fftfreq(n_cwt, dt)
# --- FFTを使って離散ウェーブレット変換する
X = np.fft.fft(x)
cwt = np.zeros((J+1, n_cwt), dtype=complex) # CWT array
Hev = np.array(omega > 0.0)
for j in range(J+1):
Psi = np.sqrt(2.0*np.pi*s[j]/dt)*np.pi**(-0.25)*np.exp(-(s[j]*omega-omega0)**2/2.0)*Hev
cwt[j, :] = np.fft.ifft(X*np.conjugate(Psi))
s_to_f = (omega0 + np.sqrt(2 + omega0**2)) / (4.0*np.pi)
freq_cwt = s_to_f / s
cwt = cwt[:, 0:len(sig)]
# --- cone of interference
COI = np.zeros_like(tm)
COI[0] = 0.5/dt
COI[1:len(tm)//2] = np.sqrt(2)*s_to_f/tm[1:len(tm)//2]
COI[len(tm)//2:-1] = np.sqrt(2)*s_to_f/(tm[-1]-tm[len(tm)//2:-1])
COI[-1] = 0.5/dt
#------------------------------------------------------------------------------
# 解析結果の可視化
figsize = (210/25.4, 294/25.4)
dpi = 200
fig = plt.figure(figsize=figsize, dpi=dpi)
# --- 図の設定 (全体)
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['xtick.top'] = True
plt.rcParams['xtick.major.size'] = 6
plt.rcParams['xtick.minor.size'] = 3
plt.rcParams['xtick.minor.visible'] = True
plt.rcParams['ytick.direction'] = 'in'
plt.rcParams['ytick.right'] = True
plt.rcParams['ytick.major.size'] = 6
plt.rcParams['ytick.minor.size'] = 3
plt.rcParams['ytick.minor.visible'] = True
plt.rcParams["font.size"] = 14
plt.rcParams['font.family'] = 'Helvetica'
# プロット枠 (axes) の設定
ax1 = fig.add_axes([0.15, 0.55, 0.70, 0.3])
ax_sc = fig.add_axes([0.15, 0.2, 0.70, 0.30])
cx_sc = fig.add_axes([0.87, 0.2, 0.02, 0.30])
# 元データのプロット
ax1.set_xlim(tms, tme)
ax1.set_xlabel('')
ax1.tick_params(labelbottom=False)
ax1.set_ylabel('x')
ax1.plot(tm, sig, c='black')
# スペクトログラムのプロット
ax_sc.set_xlim(tms, tme)
ax_sc.set_xlabel('time (s)')
ax_sc.tick_params(labelbottom=True)
ax_sc.set_ylim(0, freq_upper)
ax_sc.set_ylabel('frequency\n(Hz)')
# カラーバーのレンジの設定
norm = mpl.colors.Normalize(vmin=np.log10(np.abs(cwt[freq_cwt < freq_upper, :])**2).min(),
vmax=np.log10(np.abs(cwt[freq_cwt < freq_upper, :])**2).max())
# カラーマップ
cmap = mpl.cm.jet
# スカログラムのプロット
ax_sc.contourf(tm, freq_cwt, np.log10(np.abs(cwt)**2),
norm=norm, levels=256, cmap=cmap)
# Cone of Interference のプロット
ax_sc.fill_between(tm, COI, fc='w', hatch='x', alpha=0.5)
ax_sc.plot(tm, COI, '--', color='black')
# 右上の文字
ax_sc.text(0.99, 0.97, "scalogram", color='white', ha='right', va='top',
path_effects=[path_effects.Stroke(linewidth=2, foreground='black'),
path_effects.Normal()],
transform=ax_sc.transAxes)
mpl.colorbar.ColorbarBase(cx_sc, cmap=cmap,
norm=norm,
orientation="vertical",
label='log amplitude')
# 図を保存
plt.savefig(out_fig_path, transparent=False)実際にコードを実行してみよう
上で記述したコードは cwt-demo.pyという名前のファイルとして,好きなディレクトリ(ここでは~/Desktop/LabCode/python/cwtとします)に保存します。
ターミナルを開き,
$ cd ~/Desktop/LabCode/python/cwtと入力し,ディレクトリを移動します。あとは以下のコマンドで cwt-demo.pyを実行するだけです。( $マークは無視してください)。
$ python3 cwt-demo.py実行結果
~/Desktop/LabCode/python/cwt にscalogram.pngというファイルができて,以下のようになっていれば成功です。
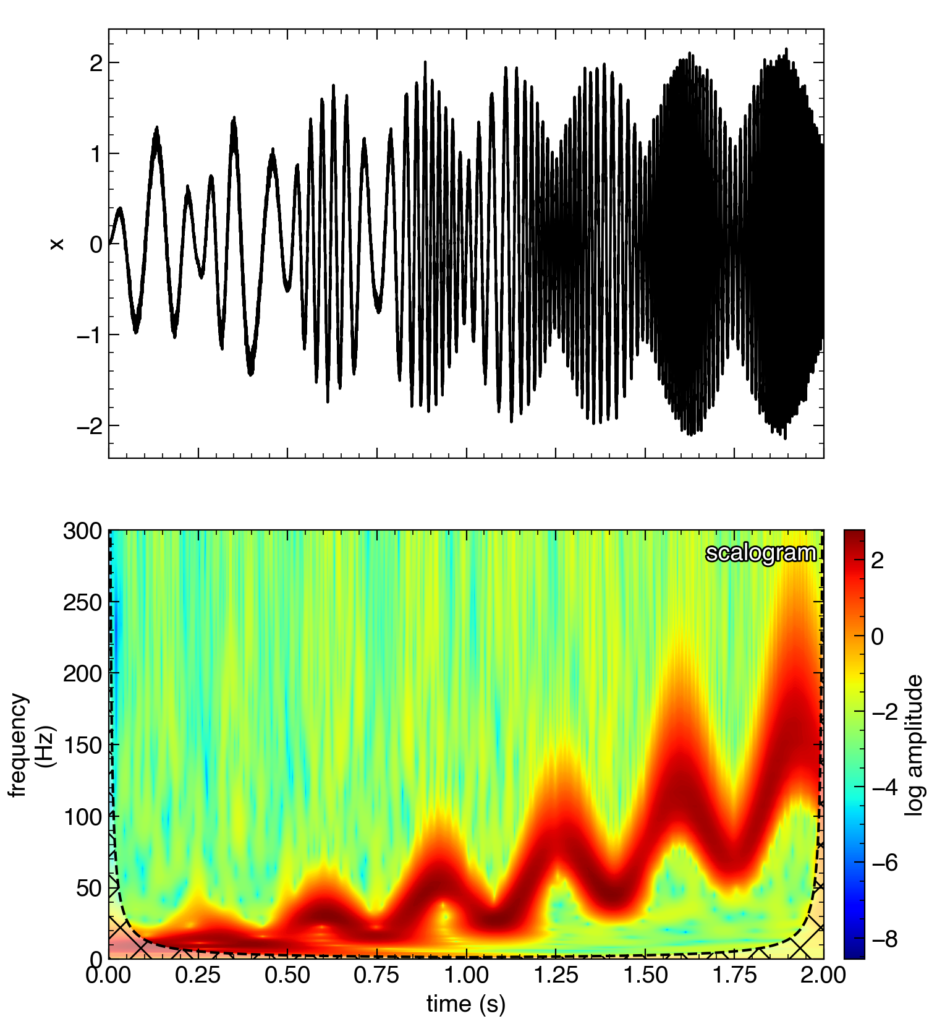
一段目は周波数と振幅が時間的に変化するテスト入力信号,二段目はスカログラムです。周波数と振幅の時間変化を追うことができていると思います!
右下と左下にみえるハッチをしてある部分はCOIの部分で,この部分はデータが有限であるためにスカログラムがエッジの部分の影響を受けていることを示しています。この部分の信頼度は低いです。
また,高周波の領域は低周波の領域と比べて上下に大きく広がっており,周波数分解能が悪いことがわかります(ただし時間分解能は良くなっています)。
コードの解説
作成したコードの解説をしていきます。
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.patheffects as path_effects
import numpy as np必要なモジュールをインポートします。
#------------------------------------------------------------------------------
# テスト信号の生成
#------------------------------------------------------------------------------
dt = 1.0e-4
tms = 0.0
tme = 2.0
tm = np.arange(tms, tme, dt)
amp = abs(np.sin(2.0*np.pi*2.0*tm)) + np.tanh(tm)
freq = 10.0 + 10.0*tm*tm + np.cos(2.0*np.pi*3.0*tm)
sig = amp*np.sin(2.0*np.pi*freq*tm) + amp*5.0e-2*np.random.randn(len(tm))テスト信号を作成します。振幅と振動数が時間的に変化するものを用います。ノイズも加えてより現実的にしておきます。
#------------------------------------------------------------------------------
# 諸々の設定
freq_upper = 300.0 # in kHz
out_fig_path = "scalogram.png" スカログラムの周波数上限の設定や出力される図の名前の設定です。
#------------------------------------------------------------------------------
# 連続ウェーブレット変換
# --- n_cwt をlen(sig)よりも大きな2のべき乗の数になるように設定
n_cwt = int(2**(np.ceil(np.log2(len(sig)))))
# --- 後で使うパラメータを定義
dj = 0.125
omega0 = 6.0
s0 = 2.0*dt
J = int(np.log2(n_cwt*dt/s0)/dj)
# --- スケール
s = s0*2.0**(dj*np.arange(0, J+1, 1))
# --- n_cwt個のデータになるようにゼロパディングをして,DC成分を除く
x = np.zeros(n_cwt)
x[0:len(sig)] = sig[0:len(sig)] - np.mean(sig)
# --- omega array
omega = 2.0*np.pi*np.fft.fftfreq(n_cwt, dt)
# --- FFTを使って離散ウェーブレット変換する
X = np.fft.fft(x)
cwt = np.zeros((J+1, n_cwt), dtype=complex) # CWT array
Hev = np.array(omega > 0.0)
for j in range(J+1):
Psi = np.sqrt(2.0*np.pi*s[j]/dt)*np.pi**(-0.25)*np.exp(-(s[j]*omega-omega0)**2/2.0)*Hev
cwt[j, :] = np.fft.ifft(X*np.conjugate(Psi))
s_to_f = (omega0 + np.sqrt(2 + omega0**2)) / (4.0*np.pi)
freq_cwt = s_to_f / s
cwt = cwt[:, 0:len(sig)]
# --- cone of interference
COI = np.zeros_like(tm)
COI[0] = 0.5/dt
COI[1:len(tm)//2] = np.sqrt(2)*s_to_f/tm[1:len(tm)//2]
COI[len(tm)//2:-1] = np.sqrt(2)*s_to_f/(tm[-1]-tm[len(tm)//2:-1])
COI[-1] = 0.5/dtウェーブレット変換の部分です。上で説明したように畳み込み定理を用いてFFTを使って計算しています。
#------------------------------------------------------------------------------
# 解析結果の可視化
figsize = (210/25.4, 294/25.4)
dpi = 200
fig = plt.figure(figsize=figsize, dpi=dpi)
# --- 図の設定 (全体)
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['xtick.top'] = True
plt.rcParams['xtick.major.size'] = 6
plt.rcParams['xtick.minor.size'] = 3
plt.rcParams['xtick.minor.visible'] = True
plt.rcParams['ytick.direction'] = 'in'
plt.rcParams['ytick.right'] = True
plt.rcParams['ytick.major.size'] = 6
plt.rcParams['ytick.minor.size'] = 3
plt.rcParams['ytick.minor.visible'] = True
plt.rcParams["font.size"] = 14
plt.rcParams['font.family'] = 'Helvetica'
# プロット枠 (axes) の設定
ax1 = fig.add_axes([0.15, 0.55, 0.70, 0.3])
ax_sc = fig.add_axes([0.15, 0.2, 0.70, 0.30])
cx_sc = fig.add_axes([0.87, 0.2, 0.02, 0.30])
# 元データのプロット
ax1.set_xlim(tms, tme)
ax1.set_xlabel('')
ax1.tick_params(labelbottom=False)
ax1.set_ylabel('x')
ax1.plot(tm, sig, c='black')
# スペクトログラムのプロット
ax_sc.set_xlim(tms, tme)
ax_sc.set_xlabel('time (s)')
ax_sc.tick_params(labelbottom=True)
ax_sc.set_ylim(0, freq_upper)
ax_sc.set_ylabel('frequency\n(Hz)')
# カラーバーのレンジの設定
norm = mpl.colors.Normalize(vmin=np.log10(np.abs(cwt[freq_cwt < freq_upper, :])**2).min(),
vmax=np.log10(np.abs(cwt[freq_cwt < freq_upper, :])**2).max())
# カラーマップ
cmap = mpl.cm.jet
# スカログラムのプロット
ax_sc.contourf(tm, freq_cwt, np.log10(np.abs(cwt)**2),
norm=norm, levels=256, cmap=cmap)
# Cone of Interference のプロット
ax_sc.fill_between(tm, COI, fc='w', hatch='x', alpha=0.5)
ax_sc.plot(tm, COI, '--', color='black')
# 右上の文字
ax_sc.text(0.99, 0.97, "scalogram", color='white', ha='right', va='top',
path_effects=[path_effects.Stroke(linewidth=2, foreground='black'),
path_effects.Normal()],
transform=ax_sc.transAxes)
mpl.colorbar.ColorbarBase(cx_sc, cmap=cmap,
norm=norm,
orientation="vertical",
label='log amplitude')
# 図を保存
plt.savefig(out_fig_path, transparent=False)解析結果を可視化しています。この部分はSTFTのものとほとんど同じです。
STFTには無いCOIの部分は, fill_between を用いてCOI以下の部分のハッチを描画を,通常のplotを用いてCOI曲線の描画を行っています。
最後に
今回は,時間周波数解析の手法の一つであるウェーブレット解析について紹介しました。STFTと比べて窓関数幅の選択の必要がないなどの利点があります。
解析の目的,信号の特性に合わせて,適切な手法を選べるようにしましょう!
(2023/05/16追記)
Morletのマザーウェーブレットの周波数空間での表現が,単純なFourier変換でない理由について
Morletのマザーウェーブレットの周波数空間での表現には,ヘヴィサイドの階段関数が含まれています。これは,マザーウェーブレットを単純にFourier変換しただけでは出てきません。
この表式は,参考文献 ([Torrence & Compo, 1998]) にあるTABLE 1を参考にしたものです。Morletのウェーブレットが周波数空間でこのような表現になる理由ですが,[Torrence & Compo, 1998]の論文には詳しく書かれていないようですので,Reference にある[Farge, 1992]の論文を参考にして説明を加えます。
本文には書きませんでしたが,どんな関数でもマザーウェーブレットとなれるわけではなく,許容性の条件 (admissibility condition) というものがあり,これを満たす必要があります。これは,式で書くと
$$
\int_{-\infty}^{+\infty} \frac{|\Psi(\omega)|^2}{|\omega|}\mathrm{d}\omega < \infty
$$
というものです。これは,また,(可積分などの条件を満たせば)
$$
\Psi(0) = 0
$$
と書くことができます[Farge, 1992]。上で述べたMorletのウェーブレットは,厳密には,許容性の条件を満たしません。そこで,修正の項を付け加えて
$$
\psi(t) = \pi^{-1/4} (e^{i\omega_0 t}-e^{-\omega_0^2/2}) e^{-t^2/2}
$$
とするものがあります。そのFourier変換は
$$
\Psi(\omega) = \pi^{-1/4} \left(e^{-(\omega_0-\omega)^2/2}-e^{-(\omega_0^2+\omega^2)/2}\right)
$$
と計算でき,$\Psi(0)=0$となって,許容性の条件を満たすことができます(これもMorletのウェーブレットと呼ばれ,Wikipediaで検索するとこの表式が出てきます (2023/05/16閲覧))。ただし,修正項はかなり小さく,$\omega_0 = 6$の場合,数値誤差と同じオーダになるため,実用上はこの修正項は付け加えられないことが多いようです。
許容性の条件を満たすように修正する別の方法として,周波数空間で直接$\Psi(0)=0$を課すこともできます。Fargeの論文には$\omega > 0$のときは単純にフーリエ変換したものとし,$\omega\le 0$の場合は0とする,本文で示した表現と同等のものが載っています ([Farge, 1992]の式(24))。[Torrence & Compo1998]のTABLE 1はこの表現を採用しているようです。
参考文献
- C. Torrence and G. P. Compo, “A Practical Guide to Wavelet Analysis”, Bull. Amer. Meteor. Soc. 79, 61 (1998): https://journals.ametsoc.org/view/journals/bams/79/1/1520-0477_1998_079_0061_apgtwa_2_0_co_2.xml
- M. Farge, “Wavelet Transforms and Their Applications to Turbulence”, Annu. Rev. Fluid Mech. 24, 395 (1992).

【技術書】Pythonを用いた時間-周波数解析入門
~フーリエ・ウェーブレット解析を中心に~
¥2,500 → ¥1,000 今なら60%OFF!!
ソースコードを惜しみなく掲載!
理論と実践の溝を埋める良書です




急なコメント失礼致します.
マザーウェーブレットのフーリエ変換について質問させていただきます.
スケールSのマザーウェーブレットのフーリエ変換の公式におけるH(ω)とは何に対応するものでしょうか?
平見樹哉さま
ご質問ありがとうございます。
H(ω)はヘヴィサイド (Heaviside) の階段関数で,ω > 0 のときH(ω) = 1でそれ以外のときはH(ω) = 0となる関数です。
この表式は,参考文献 ([Torrence & Compo, 1998]) にあるTABLE 1を参考にしたものです。
ただし,H(ω)はMorletのマザーウェーブレットのフーリエ変換から出てくるものではありません。
したがって,ご質問はご尤もで,「スケールsのMorletのウェーブレットψ_M(t/s)のフーリエ変換は」とする記述は正確ではありませんでした。
「(許容性の条件を満たすように修正した)スケールsのMorletのウェーブレットψ_M(t/s)の周波数空間での表現は」とするべきなので,お詫びして記事を修正します。
記事の最後に,H(ω)が出てくる理由について説明を加えましたので,ご興味がありましたら参照してください。
説明にご納得いただければ幸いです。
今後も記事の内容をよりわかりやすいよう工夫していきたいと思いますので,よろしくお願いいたします。