【コード付き】双曲形の偏微分方程式の数値解法【Python】

本記事では、双曲形偏微分方程式の数値解法について、分かりやすい具体例とともに掘り下げていきます。Pythonを活用したアプローチ方法を学びます。

本記事を通して偏微分方程式の数値解法の1つを会得しましょう！

注）差分法の一部の話だけにとどめています。誤差や境界条件などの詳細な議論は冗長化を避けるためにご紹介していません。

動作検証済み環境

macOS Monterey(12.7.1), python3.11.4

Pythonで学ぶ偏微分方程式の数値シミュレーションの技術書を販売中

¥2,500 → ¥1,000 今なら60%OFF!!

計算方法、グラフやアニメーションの作成方法、計算ログの残し方を惜しみなく解説しています！
理論と実装の溝を埋めてくれる良書です！

技術書ページへ

偏微分方程式の数値解法とは

偏微分方程式の数値解法は、偏微分方程式（PDE: Partial Differential Equations）の解を近似的に求めるための手法のことを指します。これらの方程式は、多くの場合、解析的な解が見つけられないため、数値的な手法が必要となります。以下に、主な数値解法をいくつか紹介します。

有限差分法（Finite Difference Method）: 空間や時間を離散的なグリッドに分割し、微分を差分に置き換えることにより近似します。この方法は直感的で実装が比較的簡単ですが、グリッドの選択が解の精度に大きく影響します。
有限要素法（Finite Element Method）: 問題の領域を小さな「要素」に分割し、各要素内で方程式を近似します。この方法は複雑な形状や境界条件を持つ問題に適しています。
有限体積法（Finite Volume Method）: 保存則を基にした方程式に特に適しており、領域を小さな「体積」に分割し、各体積内の平均値を計算します。
スペクトル法（Spectral Method）: 方程式を異なる周波数の波形の和として表し、これらの波形の係数を計算することで解を近似します。高い精度を達成できますが、滑らかな解が必要です。
差分時間領域法（Finite-Difference Time-Domain, FDTD）: 電磁気学で広く使われている、時間領域における有限差分法の一種です。

これらの方法は、物理学、工学、気象学など様々な分野で偏微分方程式の解を求めるために用いられます。それぞれの方法には特徴や適用できる問題の種類が異なり、問題の性質に応じて最適な方法を選択する必要があります。また、高度なコンピュータシミュレーションにおいては、これらの方法が組み合わされることもあります。

本記事では有限差分法（Finite Difference Method）を用いた数値解法についてご紹介します。

差分近似

偏微分方程式の数値解法においては差分法は非常に多く用いられます。

差分法では差分近似を用います。偏微分係数での差分近似の考え方の詳細は別の記事に譲り、ここでは本記事のメイントピックである双曲形方程式で使用する差分近似のみを手短にご紹介します。

$u = u(x,y)$ が領域 $0 \leqq x \leqq a, 0 \leqq y \leqq b$ で与えられているものとします。この領域を以下の図のように格子（差分格子）に分割します。格子間隔は等間隔でもよいですが、一般的には図のように不等間隔格子を用いてもよいです。

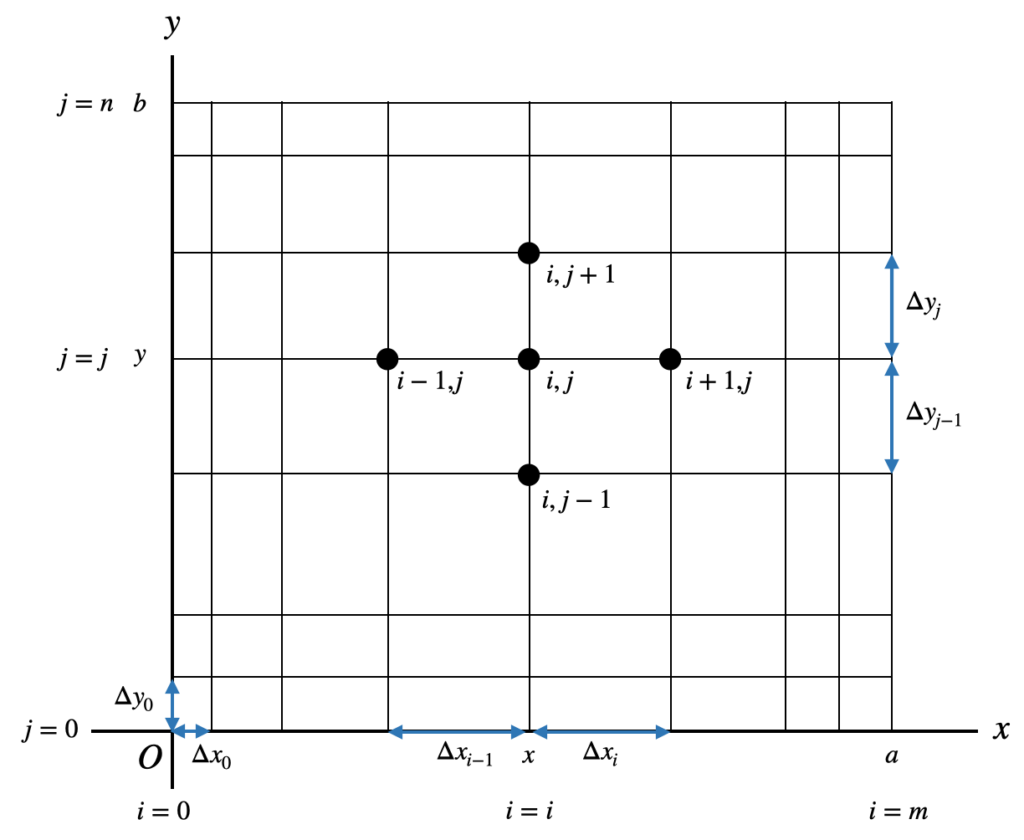
$x$ 方向への格子番号を $i=0 \sim m$ 、$y$ 方向格子番号を $j=0 \sim n$ とします。点 $(x,y)$ の格子点の番号を図に示したように $(i,j)$ とし、そこでの $u$ の値 $u(x,y)$ を $u_{i,j}$ と表します。格子点 $(i,j)$ の隣の格子点は図に示したように $\Delta x_i,\Delta y_i$ などで表しておきます。

格子間隔が等間隔の場合は

$$
\begin{aligned}
\Delta x_{i-1} = \Delta x_{i} =h \\
\Delta y_{i-1} = \Delta y_{i} =k
\end{aligned}
$$

となり、1階偏微分係数は中心差分近似を用いて次のようになります。

$$
\begin{aligned}
\frac{∂u}{∂x} = \frac{1}{2h}(u_{i+1,j} – u_{i-1,j}) \\
\frac{∂u}{∂y} = \frac{1}{2k}(u_{i,j+1} – u_{i,j-1})
\end{aligned}
$$

また2階偏微分係数は中心差分近似を用いて次のようになります。

$$
\begin{align*}
\frac{∂^2u}{∂x∂y} &= \frac{1}{4hk}(u_{i+1,j+1} – u_{i+1,j-1} – u_{i-1,j+1} + u_{i-1,j-1}) \\
\frac{∂^2u}{∂x^2} &= \frac{1}{h^2}(u_{i+1,j} – 2u_{i,j} + u_{i-1,j}) \\
\frac{∂^2u}{∂y^2} &= \frac{1}{k^2}(u_{i,j+1} – 2u_{i,j} + u_{i,j-1})
\end{align*}
$$

これらの差分近似を用いて、偏微分方程式を差分方程式に変換します。

有限差分法（Finite Difference Method）を用いた数値解法

有限差分法を用いた偏微分方程式を数値的に解く手順としては、

偏微分方程式→差分方程式へ変換
差分方程式を使って、各要素の値を計算していく

となります。以下でそれぞれの手順について説明します。

偏微分方程式→差分方程式へ変換

双曲形方程式

$$
\frac{∂^2u}{∂t^2} = p(x,t) \frac{∂^2u}{∂x^2} + q(x,t); \ \ \ \ \ \ 0 \leqq x \leqq a, 0 \leqq t < \infty \ \ \ \ (1)
$$

ただし与えられた領域で $p(x,t) > 0$ とします。この方程式を

初期条件： $u(x,0)= f_1(x), \ \ ∂u/∂t |_{t=0} \equiv \frac{∂u(x,0)}{∂t} = f_2(x)$
境界条件： $u(0,t) = g_1(t), \ \ \ u(a,t) = g_2(t)$

のもとで解く場合を例に考えます。（$p(x,t), q(x,t), a, f_1(x), f_2(x), g_1(t), g_2(t)$ は既知とします）

まずは式 $(1)$ を差分方程式で表していきましょう。差分方程式への変換は前節の差分近似した偏微分係数を流用します。すなわち

$$
\frac{(u_{i,j+1} – 2u_{i,j} + u_{i,j-1}) }{k^2} = p_{i,j} \frac{(u_{i+1,j} – 2u_{i,j} + u_{i-1,j}) }{h^2} + q_{i,j}
$$

となります。この式を整理すると

$$
\begin{align*}
u_{i,j+1} &= R (u_{i+1,j} + u_{i-1,j}) + S u_{i,j} – u_{i,j-1} + Q \ \ \ \ (2) \\
R &= \frac{k^2}{h^2}p_{i,j}, \ \ S=2(1-R), \ \ Q=k^2q_{i,j}
\end{align*}
$$

となります。

差分方程式を使って、各要素の値を計算していく

差分方程式 $(2)$ をよく眺めてみましょう。

たとえば、 $u_{i,1}$ を求めたいとき、式 $(2)$ に $j=0$ を代入すると

$$
u_{i,1} = R (u_{i+1,0} + u_{i-1,0}) + S u_{i,0} – u_{i,-1} + Q \ \ \ \ (3)
$$

となります。

お気づきかもしれませんが $u_{i,-1}$ というマイナスの格子点が登場しています。
これは実際には存在しませんので、仮想格子とします。
この仮想格子は初期条件 $∂u/∂t |_{t=0} \equiv \frac{∂u(x,0)}{∂t} = f_2(x)$ を使って置き換えが可能です。

$∂u/∂t = f_2(ih)$ は差分方程式で表すと

$$
\frac{u_{i,j+1} – u_{i,j-1}}{2k} = f_2(ih)
$$

$$
u_{i,j-1} = -2kf_2(ih) + u_{i,j+1}
$$

これに $j=0$ を代入すると

$$
u_{i,-1} = u_{i,1} – 2kf_2(ih)
$$

これを $(3)$ 式に代入すると

$$ u_{i,1} = R (u_{i+1,0} + u_{i-1,0}) + S u_{i,0} – u_{i,1} + 2kf_2(ih) + Q $$

$$ u_{i,1} = \frac{1}{2} ( R (u_{i+1,0} + u_{i-1,0}) + S u_{i,0} + 2kf_2(ih) + Q ) $$

このようにすると $u_{i,1}$ の値は初期条件と境界条件により求められるようになります。

例題

次の偏微分方程式を与えられた条件のもとで解いてください。

$$
\frac{\partial^2 u}{\partial t^2} = (x + 1) \frac{\partial^2 u}{\partial x^2} + x e^{-t}; 0 \leqq x \leqq 1, 0 \leqq t < \infty
$$

初期条件： $u(x,0) = \sin \pi x, \frac{\partial u (x,0)}{\partial t} = 0$

境界条件： $u(0, t) = 0, u(1, t) = 0$

格子番号を $i=0 \sim m, j=0 \sim n$ とし、任意格子点の $u$ の値を $u_{i,j}$ とします。

上でもご紹介したように、まずはこの偏微分方程式を差分方程式に変換し、次に差分方程式を解くためのプログラムを実装していきましょう。

実装方法

コードは以下のように実装できます。

グラフの作成、結果のテキストファイル出力もしているので少しコードが長いですが、重要な部分は calculate_equation 関数になります。

以下の実装を main.py という名前でどこかのフォルダ（ここでは~/Desktop/labcode/python/numerical_calculation/hyperbolic_equationとします）に保存しましょう。

import matplotlib.pyplot as plt
from matplotlib.animation import ArtistAnimation
import numpy as np


def _set_initial_condition(
    *,
    array_2d: list,
    grid_counts_x: int,
    grid_space: float,
) -> None:
    """
    初期条件の設定

    境界以外のt=0のU値を設定する
    """
    for i in range(1, grid_counts_x):
        array_2d[i][0] = np.sin(np.pi * i * grid_space)


def _set_boundary_condition(
    *,
    array_2d: list,
    grid_counts_x: int,
    grid_counts_t: int,
) -> None:
    """境界条件の設定"""
    for j in range(grid_counts_t + 1):
        array_2d[0][j] = 0.0
        array_2d[grid_counts_x][j] = 0.0


def calculate_equation(*, M: int, N: int, H: float, K: float) -> list:
    """
    差分方程式を計算する

    本プログラムの肝となる関数
    """
    # U値のリスト
    U: list = [[0.0 for _ in range(N + 1)] for _ in range(M + 1)]

    # 初期条件設定
    _set_initial_condition(
        array_2d=U,
        grid_counts_x=M,
        grid_space=H,
    )
    # 境界条件設定
    _set_boundary_condition(
        array_2d=U,
        grid_counts_x=M,
        grid_counts_t=N,
    )

    # U[i][1]の計算
    for i in range(1, M):
        R = (K / H) ** 2 * (i * H + 1)
        S = 2 * (1.0 - R)
        Q = K**2 * i * H * np.exp(0)
        U[i][1] = (R * (U[i + 1][0] + U[i - 1][0]) + S * U[i][0] + Q) / 2.0

    # U[i][j + 1]の計算
    for j in range(1, N):
        for i in range(1, M):
            R = (K / H) ** 2 * (i * H + 1)
            S = 2 * (1.0 - R)
            Q = K**2 * i * H * np.exp(-j * K)
            U[i][j + 1] = (
                R * (U[i + 1][j] + U[i - 1][j]) + S * U[i][j] - U[i][j - 1] + Q
            )

    return U


def animate_time_evolution(
    *,
    array_2d: list,
    grid_counts_x: int,
    grid_counts_t: int,
    grid_space: float,
    time_delta: float,
) -> None:
    """
    点線プロットのアニメーションを作成
    array_1dのデータをプロットし、時間発展をアニメーションで表示する
    """
    # 2次元配列を転置
    array_2d = np.array(array_2d).T
    # x軸の値を生成
    x_values = np.arange(grid_counts_x + 1) * grid_space

    # アニメーションの作成
    path_gif = "./animation.gif"
    frames = []

    fig, ax = plt.subplots(figsize=(7, 5))
    plt.xlabel("X (m)")
    plt.ylabel("Temperature (deg.)")
    plt.grid(True)

    for j in range(grid_counts_t + 1):
        frame = plt.plot(
            x_values,
            array_2d[j],
            linestyle="--",
            marker="o",
            color="b",
        )

        time = j * time_delta
        text = ax.text(
            0.05,
            0.95,
            f"t = {time:.2f} (h)",
            transform=ax.transAxes,
            fontsize=14,
            verticalalignment="top",
        )
        frames.append(frame + [text])

    anim = ArtistAnimation(fig, frames, interval=100)
    anim.save(path_gif, writer="pillow")


def output_result_file(
    array_2d: list,
    grid_counts_x: int,
    grid_counts_t: int,
    grid_space: float,
    time_delta: float,
) -> None:
    """2次元配列をテキストファイルに書き出す"""
    with open("./calculated_result.txt", "w") as file:
        file.write(f"# This file shows calculated result as below.\n\n")
        file.write(f"# Calculation Parameters.\n")
        file.write(f"grid_counts_x: {grid_counts_x}\n")
        file.write(f"grid_counts_t: {grid_counts_t}\n")
        file.write(f"grid_space: {grid_space}\n")
        file.write(f"time_delta: {time_delta}\n\n")

        file.write(f"# Calculated Matrix U.\n")
        for row in array_2d:
            line = " ".join(map(str, row))
            file.write(line + "\n")


def validate_parameters(R: float) -> None:
    """パラメータの妥当性をチェックする"""
    if R > 1.0:
        raise ValueError("R must be less than 1.0.")


if __name__ == "__main__":
    """
    双曲形方程式の数値解法（陽解法）
    """
    grid_counts_x: int = 10  # 格子点番号mの値
    grid_counts_t: int = 40  # 格子点番号nの値
    grid_space: float = 0.1  # 刻み幅 (meter)
    time_delta: float = 0.05  # 刻み幅 (hour)

    validate_parameters(R=2 * (time_delta / grid_space))

    array_2d = calculate_equation(
        M=grid_counts_x,
        N=grid_counts_t,
        H=grid_space,
        K=time_delta,
    )
    animate_time_evolution(
        array_2d=array_2d,
        grid_counts_x=grid_counts_x,
        grid_counts_t=grid_counts_t,
        grid_space=grid_space,
        time_delta=time_delta,
    )
    output_result_file(
        array_2d=array_2d,
        grid_counts_x=grid_counts_x,
        grid_counts_t=grid_counts_t,
        grid_space=grid_space,
        time_delta=time_delta,
    )

プログラムを実行する

ターミナルを開き、

$ cd Desktop/labcode/python/numerical_calculation/hyperbolic_equation

と入力し、ディレクトリを移動します。あとは以下のコマンドを実行するだけです。（ $マークは無視してください）

$ python main.py

実行結果

~/Desktop/LabCode/python/numerical_calculation/hyperbolic_equationにanimation.gifというファイルができて，以下のようなgif画像になっていれば成功です！

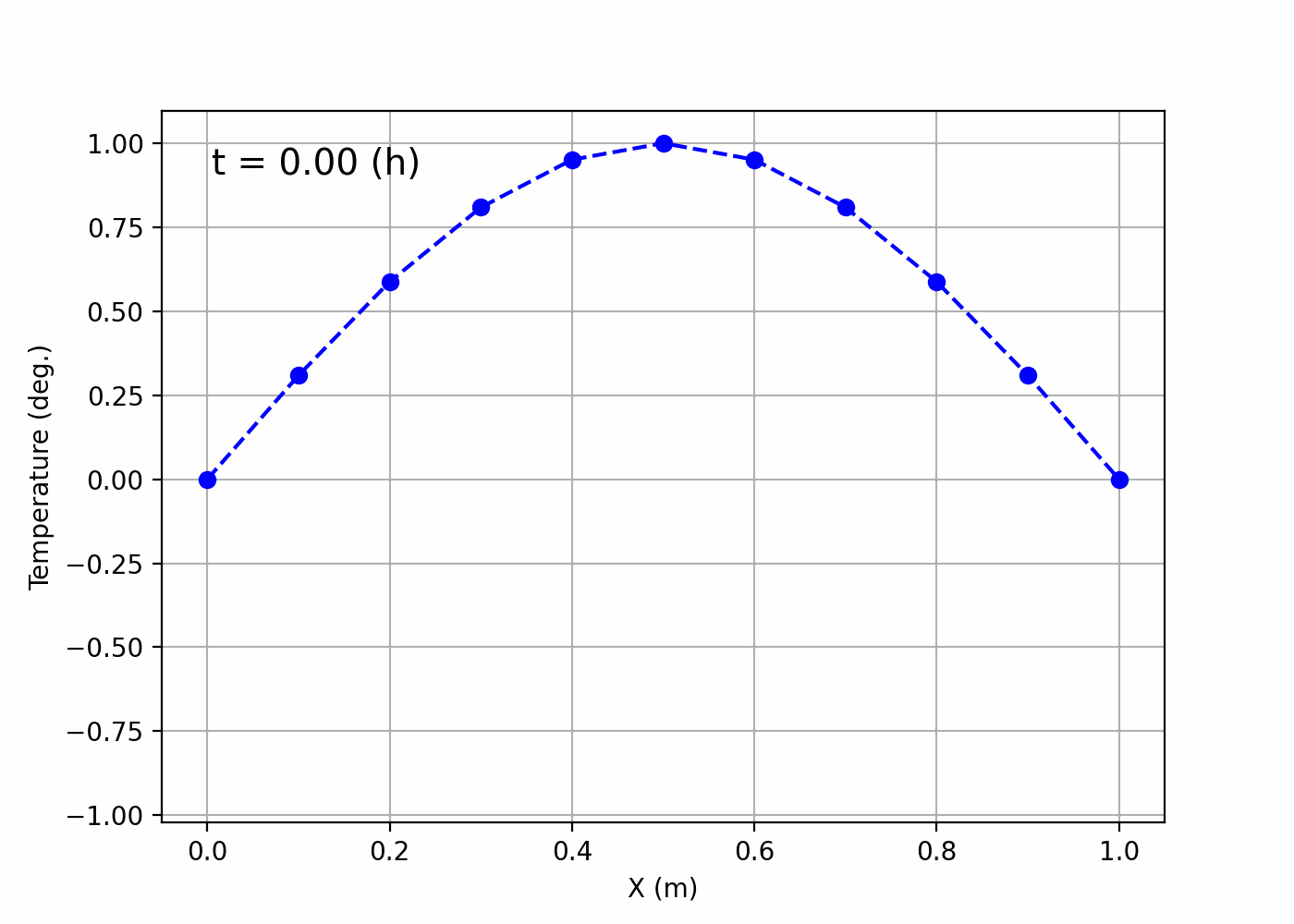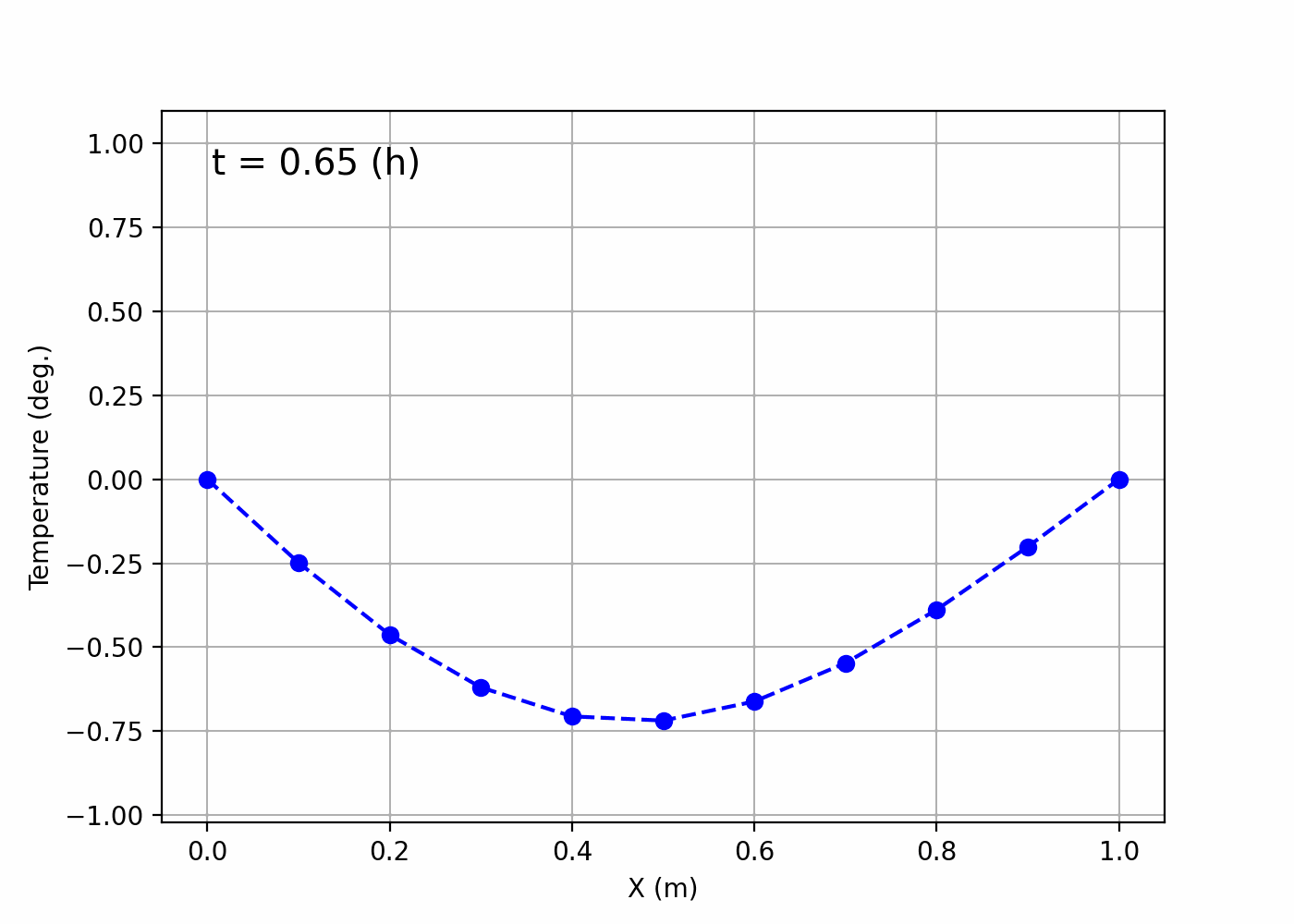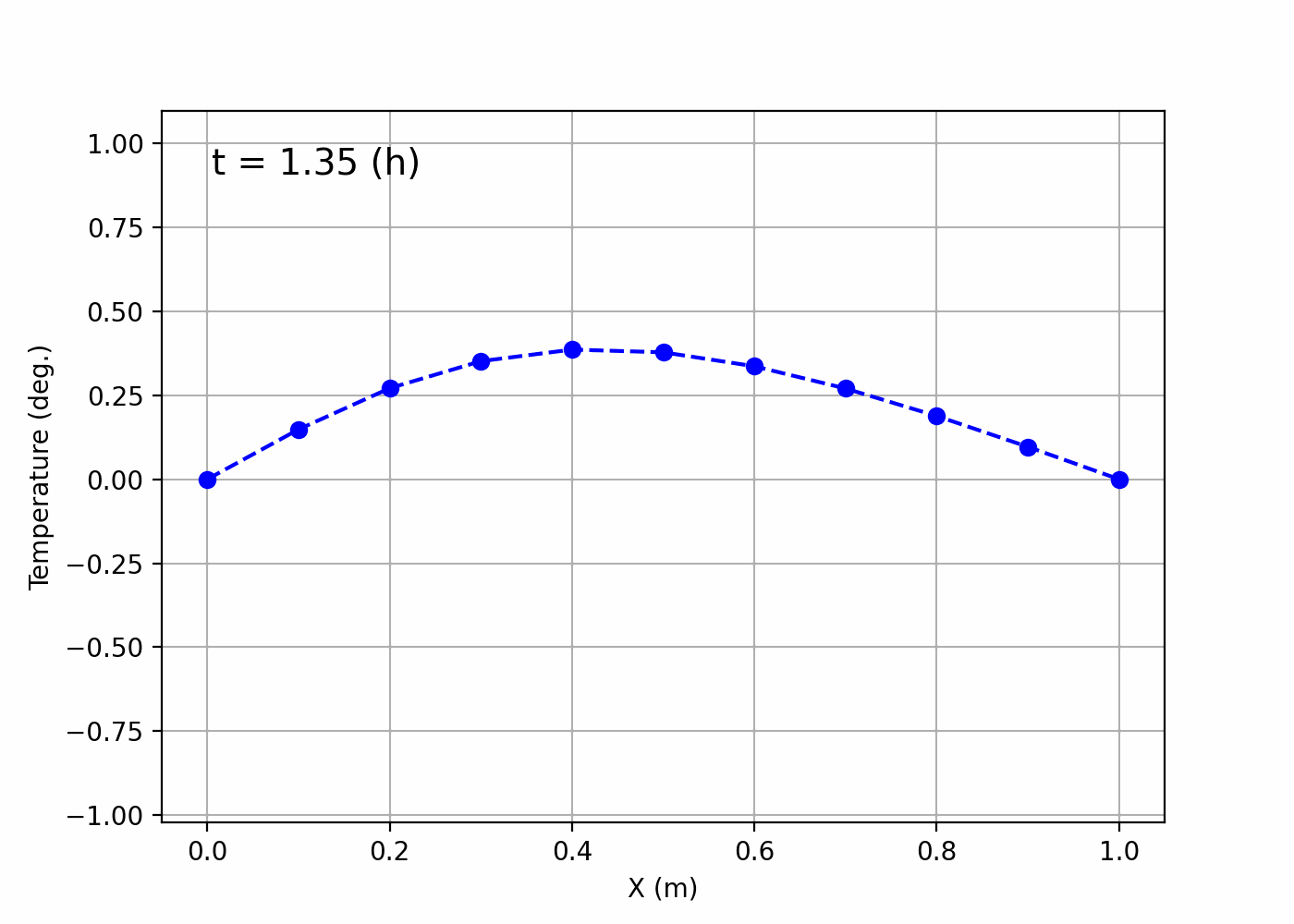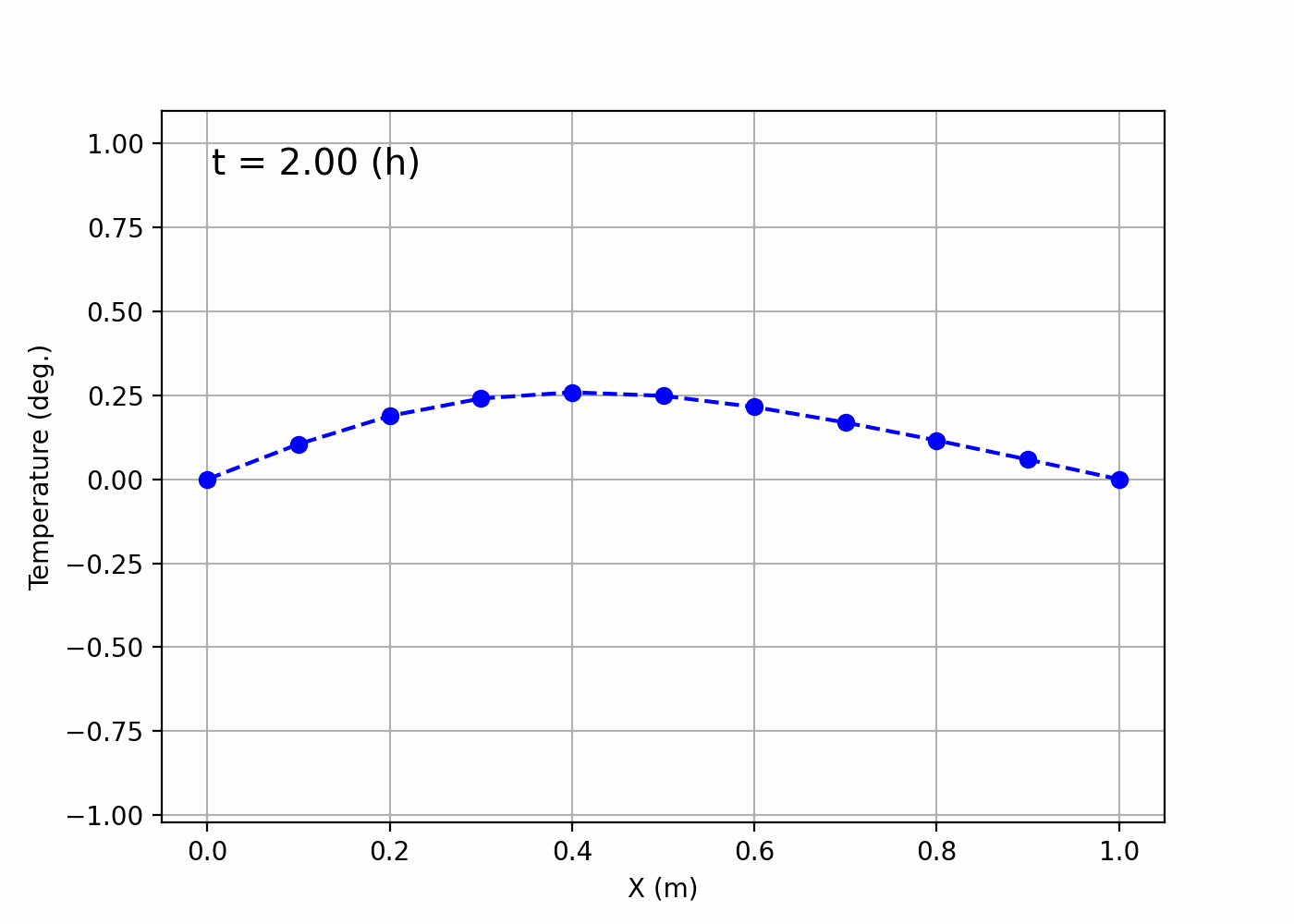
紐が上下に揺れているような様子が可視化されていますね。

また、 calculated_result.txt というテキストファイルも以下のように作成されているはずです。今回は簡単な情報しか出力していませんが、このように計算結果と計算に用いたパラメータを出力しておくことで、第三者でも計算結果を評価することが可能になります。自分のためにも、他の人のためにも、ぜひ結果は出力する癖をつけましょう。

# This file shows calculated result as below.

# Calculation Parameters.
grid_counts_x: 10
grid_counts_t: 40
grid_space: 0.1
time_delta: 0.05

# Calculated Matrix U.
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
0.3090169943749474 0.3049827931120519 0.2927821760958873 0.2722125088561874 0.24313249125986083 0.2056500846551192 0.16025988763305207 0.10790150134761026 0.049957056241041804 -0.011776227735267425 -0.07511760786572898 -0.13754506237975533 -0.19627228588447948 -0.2483850607628004 -0.2910494490618322 -0.3217810901327259 -0.33872980098363337 -0.34090019579050934 -0.32823116914706624 -0.30151830303315574 -0.26225260404213835 -0.21248646260817422 -0.15477070801737391 -0.09208545147202046 -0.02763894080408742 0.0354929092367792 0.09474601028741463 0.14825999445084737 0.19479726271990142 0.23351002385827413 0.2637698944599734 0.28516869573600334 0.2976070799025527 0.3013022383634498 0.29663949096085396 0.28395511520066646 0.26340675931670643 0.2350142105333222 0.19882915277839425 0.1551334956238426 0.10459537550306455
0.5877852522924731 0.5794047749172154 0.5543088628170679 0.5126958273460732 0.45496653998632314 0.38183656708080815 0.2945074341077582 0.19484943599137944 0.08552713473208474 -0.029979739805290357 -0.14746324136234149 -0.26215923909875755 -0.3689909509784872 -0.46288693921615043 -0.5391585312066091 -0.5938718581498124 -0.6241287517745315 -0.6282274180634483 -0.605763439910379 -0.5577415238072453 -0.4866562168746265 -0.396383366236136 -0.2917731099124619 -0.17805419410682333 -0.060332278626518375 0.05662081778466293 0.16837474844587952 0.27091443995791226 0.36091759317919675 0.43606901823037764 0.4951148730446506 0.5375611038249619 0.5632370694954658 0.5720375009427245 0.5639433483267814 0.5391559627299322 0.49813890910075964 0.4415490819280186 0.3702110635406817 0.2852559676690559 0.188369752755483
0.8090169943749473 0.7965232585985789 0.7592704092720312 0.6980237929127329 0.6141004189717728 0.5093945146429286 0.38642406640356547 0.24840854667589776 0.09936476888613366 -0.055834722193602956 -0.21152807988969136 -0.3615207126461062 -0.49950522332576336 -0.6195109064734203 -0.7162343720335208 -0.7852284593598534 -0.8230824930529504 -0.8277248504163482 -0.7987802002730451 -0.7377313435221419 -0.647714483089495 -0.5330721471620046 -0.398968098673832 -0.2512073324417034 -0.09609033703254855 0.05994066583789725 0.21083513645200833 0.3513483573947398 0.4771211681315775 0.5845518279992986 0.6707558879158749 0.7336988815915186 0.7722787841475706 0.7861374001302917 0.7752986232162671 0.7399682935790364 0.6806863155925486 0.5986612539968726 0.4959534349899685 0.3753709194551349 0.24025537802143512
0.9510565162951535 0.9352647096074655 0.8883168938922941 0.8115908705902218 0.707398671948937 0.5789566329809795 0.43033859053378526 0.2664083523469224 0.09271485434941559 -0.08468074375135591 -0.25945191243276705 -0.425265540904309 -0.5759665147347939 -0.705702002176888 -0.8091350151498963 -0.881859587589341 -0.9208833740033349 -0.9248639864377418 -0.8939530241348044 -0.8294813235011836 -0.7338510080306243 -0.6106862842452613 -0.464910581493102 -0.30245661969968485 -0.12973112835440392 0.04679463434042434 0.22072429825458287 0.38582891975040373 0.5363182858775802 0.6671807064844799 0.774309475522349 0.8543834990505005 0.9047890866094387 0.9238021290772088 0.910873696978843 0.8666822280993867 0.7928735443140164 0.6917713174935313 0.5663515818474197 0.42044054369488726 0.25883271358109905
1.0 0.9822711936106826 0.9296975356413092 0.8442239959373173 0.7290724361268137 0.5886478819981495 0.4283873604915754 0.25449973544548227 0.07357231081469656 -0.10785019025842718 -0.2835157176896811 -0.44747978393200727 -0.5940944497086907 -0.7182347301879992 -0.8157160718954938 -0.8835523744682285 -0.9198446977666628 -0.9235340944437193 -0.8943996517938706 -0.8333116640131276 -0.7423688790470901 -0.6246974464208462 -0.484151955862201 -0.32526335615056695 -0.1533745564258732 0.025412592621437396 0.2046203908818099 0.37781092316523823 0.5387338536686733 0.6813289510921626 0.7999262755006344 0.8896947338150822 0.9470295559022702 0.9696567880962499 0.9566038555838664 0.9082790516215525 0.8266069389688095 0.7149535352989325 0.5777758112030321 0.42025569355509024 0.2481638741071843
0.9510565162951536 0.9331873086520817 0.8803290347045547 0.7948467077456308 0.6806224462793355 0.5428472153973213 0.3876277936083759 0.2214693593524663 0.05087516328029061 -0.1177931342259182 -0.27839739530849683 -0.4253521250859268 -0.5541200626765675 -0.6614171073968096 -0.7448989752943701 -0.8027024384581181 -0.8333626470867074 -0.8360986806844454 -0.8109920579696874 -0.7588183487758012 -0.6808366211069099 -0.5788775799403985 -0.45558794276899 -0.3144583484645533 -0.15962636701007166 0.004197266147748216 0.17156200159373927 0.3362151876312711 0.491453210033439 0.6307012333661528 0.7479223320276944 0.8378087787275489 0.8960434637532305 0.9197241748695867 0.9076667452422327 0.8603704721577393 0.7798392279505066 0.669546774747226 0.5344550956891249 0.3807387250434341 0.21515931268026817
0.8090169943749475 0.7930636475904655 0.746007260921673 0.6703869283739219 0.5702247925685181 0.45051556859264735 0.3167426272302094 0.17470699838233988 0.030479061988168264 -0.10996709270291546 -0.24142973463836326 -0.3599210475618002 -0.4625264871037999 -0.54701921421177 -0.6117480617479326 -0.6557657406828898 -0.6787551424450636 -0.6806594321387394 -0.6614413841717108 -0.6212552661889166 -0.560740627327072 -0.481043490006875 -0.3836723034070762 -0.27058476078859867 -0.14452852663059523 -0.009239697593738739 0.13070274456064307 0.27010939203147183 0.40327283010978837 0.5241265653818611 0.62674502054998 0.7059974895527332 0.7579153248883971 0.7797260226263198 0.7699474630425529 0.7287228125991388 0.6580486236112529 0.5615523101847922 0.4440117688841584 0.31103062446964036 0.16885394055860917
0.5877852522924732 0.5758395362295867 0.5407504015846227 0.48463763790480924 0.41046274594392795 0.3218859953010506 0.2233654152717499 0.11988460987501386 0.016221129219635394 -0.0836289017909767 -0.17643877900937394 -0.2594871201240938 -0.33057457724664435 -0.38826767523267 -0.4319097498025059 -0.4612957824241638 -0.4763857874944956 -0.47728050940528305 -0.4642281854061583 -0.4374528328067261 -0.39702414075593423 -0.3430643219118048 -0.27614764846349893 -0.19750040324649684 -0.10894714505580902 -0.01290670904576693 0.08746060441845853 0.1882462320819253 0.28511304431992207 0.373679478319645 0.4496701468472645 0.5089954530337145 0.5481155236606657 0.5646094123553451 0.5574851525446628 0.527066581404044 0.47481943693561685 0.4033945681747775 0.31662174043795954 0.2191001259622241 0.11558358779491351
0.3090169943749475 0.30295791946630984 0.28475286697885804 0.2549249158047677 0.21505776556788883 0.16769768655930678 0.11567295484929299 0.06152432928306593 0.007458328790424913 -0.044479827570212765 -0.09245121274871328 -0.13503767186103538 -0.17129658769096237 -0.20061184322541958 -0.22259839043353413 -0.2371562809524509 -0.24446837647434985 -0.2448077732362381 -0.23832634379432496 -0.22502849408131198 -0.20487350327147494 -0.17784742247016966 -0.14403448329481042 -0.10380995807122258 -0.058066231490956396 -0.00823179191898847 0.04393679897221464 0.09652241447290816 0.1474119870497067 0.19424371115011552 0.234569445007957 0.2661495687210239 0.28713800028124264 0.2961544724785851 0.29244577898445734 0.2761300808429286 0.24823842344030217 0.21043141881230523 0.16468076981984328 0.11321524559981189 0.05858791455308532
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0

コードの解説

このPythonコードは、双曲形方程式（hyperbolic equation）の数値解法に関するもので、特定の条件下で方程式の近似解を計算し、その結果をアニメーションとテキストファイルに出力するものです。コードは以下に記すいくつかの主要な部分に分かれています

1. Pythonにおけるメイン実行ブロック

if __name__ == "__main__":
    """
    双曲形方程式の数値解法（陽解法）
    """
    grid_counts_x: int = 10  # 格子点番号mの値
    grid_counts_t: int = 40  # 格子点番号nの値
    grid_space: float = 0.1  # 刻み幅 (meter)
    time_delta: float = 0.05  # 刻み幅 (hour)

    validate_parameters(R=2 * (time_delta / grid_space))

    array_2d = calculate_equation(
        M=grid_counts_x,
        N=grid_counts_t,
        H=grid_space,
        K=time_delta,
    )
    animate_time_evolution(
        array_2d=array_2d,
        grid_counts_x=grid_counts_x,
        grid_counts_t=grid_counts_t,
        grid_space=grid_space,
        time_delta=time_delta,
    )
    output_result_file(
        array_2d=array_2d,
        grid_counts_x=grid_counts_x,
        grid_counts_t=grid_counts_t,
        grid_space=grid_space,
        time_delta=time_delta,
    )

このコードは、双曲形方程式の数値解法を実装したものです。具体的には、双曲形方程式の数値解を陽解法（explicit method）を用いて求め、その結果をアニメーション化し、テキストファイルに出力するプログラムです。コードの各部分の概要は以下の通りです：

グリッドと時間の設定:
- grid_counts_xとgrid_counts_tは、それぞれ空間と時間方向の格子点の数を設定します。
- grid_spaceは空間方向の格子点間の距離（刻み幅）を、time_deltaは時間方向の格子点間の時間間隔（刻み幅）を設定します。
パラメータの妥当性チェック:
- validate_parameters関数を呼び出して、計算に使用するパラメータが妥当かどうかをチェックします。ここでは、双曲形方程式の数値解法に特有の安定性条件を考慮しています。
方程式の計算:
- calculate_equation関数を呼び出し、差分方程式を計算します。この関数は、空間と時間の格子点の数、空間と時間の刻み幅に基づいて数値解を計算します。
アニメーションの作成:
- animate_time_evolution関数を呼び出して、計算結果を基にアニメーションを作成します。これにより、解の時間変化を視覚的に確認できます。
結果のファイル出力:
- output_result_file関数を呼び出して、計算された数値解をテキストファイルに出力します。

このコードのメイン部分は、双曲形方程式の数値解法の実行と結果の視覚化・出力を担っています。双曲形方程式は、波動方程式のような時間依存性を持つ偏微分方程式であり、このような数値解法は物理学や工学の多くの分野で応用されます。安定性の条件を満たすために、時間と空間の刻み幅の比率を適切に設定することが重要です。

2. パラメータの妥当性チェック

def validate_parameters(R: float) -> None:
    """パラメータの妥当性をチェックする"""
    if R > 1.0:
        raise ValueError("R must be less than 1.0.")

このvalidate_parameters関数は、数値解法において重要なパラメータRの妥当性をチェックするための関数です。双曲形方程式の数値解法で特に重要なのは、このパラメータが安定性と正確性に関連する条件を満たしているかどうかを確認することです。関数の動作は以下の通りです：

関数のパラメータ:
- R: 数値解法において使用されるパラメータです。この値は通常、空間と時間の刻み幅に依存し、数値解法の安定性に直接関わります。
妥当性チェック:
- この関数は、Rが1.0より大きい場合にエラーを発生させます。具体的には、R > 1.0の場合、ValueErrorを投げて処理を中断します。
重要性:
- この妥当性チェックは、双曲形方程式の数値解法における計算の安定性を保証するために非常に重要です。特に、差分法を用いた数値解法では、R（または類似のパラメータ）の値が安定性条件を満たさない場合、計算が不安定になり、結果が物理的に意味をなさないものになる可能性があります。

この関数は、数値解析を行う前にパラメータが適切な範囲内にあることを確認し、計算の正確性と安定性を保証するために使用されます。特に、差分法のような数値解法では、このようなパラメータのチェックが非常に重要です。

3. 差分方程式の計算

def calculate_equation(*, M: int, N: int, H: float, K: float) -> list:
    """
    差分方程式を計算する

    本プログラムの肝となる関数
    """
    # U値のリスト
    U: list = [[0.0 for _ in range(N + 1)] for _ in range(M + 1)]

    # 初期条件設定
    _set_initial_condition(
        array_2d=U,
        grid_counts_x=M,
        grid_space=H,
    )
    # 境界条件設定
    _set_boundary_condition(
        array_2d=U,
        grid_counts_x=M,
        grid_counts_t=N,
    )

    # U[i][1]の計算
    for i in range(1, M):
        R = (K / H) ** 2 * (i * H + 1)
        S = 2 * (1.0 - R)
        Q = K**2 * i * H * np.exp(0)
        U[i][1] = (R * (U[i + 1][0] + U[i - 1][0]) + S * U[i][0] + Q) / 2.0

    # U[i][j + 1]の計算
    for j in range(1, N):
        for i in range(1, M):
            R = (K / H) ** 2 * (i * H + 1)
            S = 2 * (1.0 - R)
            Q = K**2 * i * H * np.exp(-j * K)
            U[i][j + 1] = (
                R * (U[i + 1][j] + U[i - 1][j]) + S * U[i][j] - U[i][j - 1] + Q
            )

    return U

このcalculate_equation関数は、双曲形偏微分方程式の数値解法を実装しているものです。この関数は差分方程式を用いて、与えられた初期条件と境界条件のもとで方程式の数値解を計算します。関数の動作は以下の通りです：

関数のパラメータ:
- M: 空間方向の格子の数です。
- N: 時間方向の格子の数です。
- H: 空間方向の格子点間の距離（刻み幅）です。
- K: 時間方向の格子点間の時間間隔（刻み幅）です。
U値の初期化:
- U: 2次元リスト（配列）で、計算される各格子点の値を格納します。初期値は全て0.0に設定されています。
初期条件と境界条件の設定:
- _set_initial_condition関数と_set_boundary_condition関数を使用して、Uの初期条件と境界条件を設定します。
U[i][1]の計算:
- 第一時間ステップにおけるUの値を計算します。この計算では、特定の数学的な関係（ここで定義されているR、S、Qを使用）を用いています。
U[i][j + 1]の計算:
- 第二時間ステップ以降のUの値を計算します。このループでは、各時間ステップにおいて空間格子点に対するUの値を更新します。
結果の返却:
- 計算されたUの値の2次元リストを返します。

この関数は、与えられた初期条件と境界条件のもとで双曲形方程式の数値解を計算することを目的としています。特に、この種の計算は波動方程式のような時間依存性を持つ物理現象をモデル化する際に重要です。数値解法の正確性と安定性を保証するために、適切な刻み幅と時間間隔を選択することが重要です。

4. アニメーションの作成

def animate_time_evolution(
    *,
    array_2d: list,
    grid_counts_x: int,
    grid_counts_t: int,
    grid_space: float,
    time_delta: float,
) -> None:
    """
    点線プロットのアニメーションを作成
    array_1dのデータをプロットし、時間発展をアニメーションで表示する
    """
    # 2次元配列を転置
    array_2d = np.array(array_2d).T
    # x軸の値を生成
    x_values = np.arange(grid_counts_x + 1) * grid_space

    # アニメーションの作成
    path_gif = "./animation.gif"
    frames = []

    fig, ax = plt.subplots(figsize=(7, 5))
    plt.xlabel("X (m)")
    plt.ylabel("Temperature (deg.)")
    plt.grid(True)

    for j in range(grid_counts_t + 1):
        frame = plt.plot(
            x_values,
            array_2d[j],
            linestyle="--",
            marker="o",
            color="b",
        )

        time = j * time_delta
        text = ax.text(
            0.05,
            0.95,
            f"t = {time:.2f} (h)",
            transform=ax.transAxes,
            fontsize=14,
            verticalalignment="top",
        )
        frames.append(frame + [text])

    anim = ArtistAnimation(fig, frames, interval=100)
    anim.save(path_gif, writer="pillow")

このanimate_time_evolution関数は、数値的に解かれた偏微分方程式（例えば、双曲形方程式）の結果をアニメーションとして視覚化するための関数です。具体的な機能とプロセスは以下の通りです：

パラメータ:
- array_2d: 2次元の数値データを格納したリスト。これは計算結果を含みます。
- grid_counts_x: 空間方向の格子点の数。
- grid_counts_t: 時間方向の格子点の数。
- grid_space: 空間方向の格子点間の距離（刻み幅）。
- time_delta: 時間方向の格子点間の時間間隔（刻み幅）。
2次元配列の転置とx軸値の生成:
- 数値データをnumpy配列に変換し、転置します。これにより、行が時間ステップ、列が空間ステップに対応するようになります。
- x軸の値を生成します。これは、空間格子点に対応する実際の位置を示します。
アニメーションの準備:
- 出力するアニメーションファイルのパスを設定します（ここでは"./animation.gif"）。
- 各フレームを格納するための空のリストframesを作成します。
グラフの設定:
- matplotlibを使用してグラフを作成します。
- x軸（位置）とy軸（計算された値、例えば温度など）のラベルを設定します。
- グリッドを表示するためにplt.grid(True)を呼び出します。
各時間ステップでのフレームの生成:
- 時間の各ステップに対して、その時点での計算結果（例えば、温度分布）をプロットします。
- 点線とマーカーでプロットを行い、色を青（"b"）に設定します。
- 各フレームに時間を表示するテキストを追加します。
アニメーションの作成と保存:
- ArtistAnimationを使用して、フレームのリストからアニメーションを作成します。
- 作成したアニメーションをGIF形式で保存します。

この関数の目的は、計算結果の時間発展を視覚的に表現することで、データをより理解しやすくすることにあります。特に物理学や工学の分野において、このような視覚化は理解を深めるのに非常に有効です。

5. 結果のファイル出力

def output_result_file(
    array_2d: list,
    grid_counts_x: int,
    grid_counts_t: int,
    grid_space: float,
    time_delta: float,
) -> None:
    """2次元配列をテキストファイルに書き出す"""
    with open("./calculated_result.txt", "w") as file:
        file.write(f"# This file shows calculated result as below.\n\n")
        file.write(f"# Calculation Parameters.\n")
        file.write(f"grid_counts_x: {grid_counts_x}\n")
        file.write(f"grid_counts_t: {grid_counts_t}\n")
        file.write(f"grid_space: {grid_space}\n")
        file.write(f"time_delta: {time_delta}\n\n")

        file.write(f"# Calculated Matrix U.\n")
        for row in array_2d:
            line = " ".join(map(str, row))
            file.write(line + "\n")

このoutput_result_file関数は、計算された2次元配列のデータをテキストファイルに書き出すためのものです。この関数は、偏微分方程式の数値解法によって得られた結果を保存するのに使用されます。具体的な機能とプロセスは以下の通りです：

関数のパラメータ:
- array_2d: 計算された2次元配列（リスト）。これは数値解法の結果を含みます。
- grid_counts_x: 空間方向の格子点の数。
- grid_counts_t: 時間方向の格子点の数。
- grid_space: 空間方向の格子点間の距離（刻み幅）。
- time_delta: 時間方向の格子点間の時間間隔（刻み幅）。
テキストファイルの作成と書き込み:
- open関数を使用して、"./calculated_result.txt"という名前の新しいテキストファイルを書き込みモードで開きます。
- withステートメントを使うことで、ファイルの正しいクローズを保証しています。
計算パラメータの書き込み:
- ファイルに計算に使用されたパラメータ（格子点の数、格子間の距離、時間間隔）を書き込みます。これにより、ファイルの内容を見た人が計算条件を容易に理解できます。
計算結果の書き込み:
- 計算された2次元配列（array_2d）の各行をテキストファイルに書き込みます。
- 各行の数値は空白で区切られ、str関数を使用して文字列に変換されます。