はじめに
ここ最近、大雨のニュースを見るたびに「〇〇年に一度の大雨」という表現を目にします。これは「千年に一人の美少女」や「百年に一度の逸材」といったレトリックではなく、データに基づいて統計的に算出された根拠のある数字です。
気象庁や自治体では観測結果をもとにこのような量を算出し、発表することで防災に役立てています。このシリーズでは、算出方法を確認し、Pythonを使って、実装・計算してみたいと思います。
なお、ここで紹介する手法は、実際に公的機関が発表しているものとは異なる場合が多分にありますので、十分にご注意ください。
今回は、前回に引き続き、分布関数をヒストグラムに当てはめる方法について紹介したいと思います。
macOS Monterey 12.6.2, Python 3.9.15, SciPy 1.11.2
Pythonでやってみる気象データ解析の技術書を販売中
¥2,500 → ¥1,500 今なら40%OFF!!
気象の勉強をされている方必読!
気象予報士でもある著者がわかりやすく解説
プログラムを公開しているのでお手元で試せます!
「○○年に一度の大雨」の計算方法とは?
気象庁は観測結果をもとに、各地点について「〇〇年に一度の降水量」を算出し、発表しています。
ある期間内に1回起こると考えられる降水量のことを確率降水量といいます。気象庁の解説ページでは、確率降水量の推定方法が解説されていますので、これに基づいて「〇〇年に一度の大雨」の値を計算してみたいと思います。
大まかには次のような流れになっています。
- 年最大日降水量のヒストグラムを作成する
- 分布関数を当てはめる
- 分布関数の当てはまり具合を確認する
- 当てはめた分布関数から確率降水量を算出する
今回は、上記2. の「分布関数を当てはめる」を実際にやってみましょう!
当てはめる分布関数
気象庁の解説ページにあるように、当てはめに用いられる分布関数は次の5種類です。
- グンベル分布
- 一般化極値 (GEV) 分布
- 平方根指数型最大値分布
- 対数ピアソンⅢ型分布
- 対数正規分布
気象庁では、まず、1から3の分布関数を当てはめてみて、当てはまりが悪い場合には4と5の分布関数を当てはめるようです。
分布関数のパラメータ推定の手法
問題設定
問題設定は次のようになります:
確率変数 $X$ が、あるパラメータ $\boldsymbol{\theta}$ をもつ確率分布 $f(x; \boldsymbol{\theta})$ に従うとします (今考えている例では、確率変数 $X$ としては年最大日降水量で、確率分布としてはグンベル分布等の分布で、パラメータ $\boldsymbol{\theta}$ はグンベル分布の場合、$\sigma$ や $\mu$ です)。 いま、確率変数の値 $x_1, x_2, \dots, x_n$ が与えられたとします (今考えている例では、これまでの観測結果から年最大日降水量の値がわかっているということです)。このとき、$\boldsymbol{\theta}$ の値を推定しなさい。
このような問題に対して、次のような手法が知られています。
- クオンタイル法
- 積率法
- 最尤法
- 岩井法
分布関数のパラメータは、母数と呼ばれます。「分布関数の当てはめ」と書いてきましたが、統計学の言葉を使うと、母数推定ということになります。詳しく勉強したい方は、このキーワードを参考に調べてみてください。
最尤法 (maximum likelihood estimation)
最尤法とは、名前の通り、「最も尤もらしい」値を推定する手法です。具体的には、尤度関数
$$ L(\boldsymbol{\theta}) = \prod_{i=1}^{n} f(x_i; \boldsymbol{\theta}) $$
を最大にする $\boldsymbol{\theta} = \boldsymbol{\theta}^*$ をパラメータ $\boldsymbol{\theta}$ の推定量とします。式で書くとすれば
$$ \boldsymbol{\theta}^* = \mathrm{argmax}_{\boldsymbol{\theta}} L(\boldsymbol{\theta})
$$
です。
具体的に求める場合には、扱いやすいように両辺の対数を取って
$$ \ln L(\boldsymbol{\theta}) = \sum_{i=1}^n \ln f(x_i;\boldsymbol{\theta}) $$
とし、$\boldsymbol{\theta}$ で微分し、$\boldsymbol{0}$ とおくことで $\boldsymbol{\theta} = \boldsymbol{\theta}^*$を求めます。上式で定義されるパラメータの関数を対数尤度関数と言います。
見かけはあまり扱いやすいように思えないかもしれませんが、掛け算が足し算の形になっており、扱いやすいです。また、対数は単調増加関数なので尤度関数の最大化は対数尤度関数の最大化と同等です。
例 (グンベル分布の場合)
例えば、グンベル分布 $f(x;\mu, \sigma)$ (以前の記事参照) の場合、尤度関数は
$$ L(\mu, \sigma) = \frac{1}{\sigma^n}\prod_{i=1}^{n} \exp\left\{-\left(\frac{x_i-\mu}{\sigma}\right)-\exp\left[-\left(\frac{x_i-\mu}{\sigma}\right)\right]\right\} $$
対数尤度関数は
$$ \ln L(\mu, \sigma) = -n\ln\sigma -\sum_{i=1}^{n}\frac{x_i – \mu}{\sigma} – \sum_{i=1}^{n}\exp\left(-\frac{x_i – \mu}{\sigma}\right) $$
となります。これを $\mu$ と $\sigma$ でそれぞれ偏微分すると
$$ \frac{\partial (\ln L)}{\partial \mu} =\frac{n}{\sigma} – \frac{1}{\sigma}\sum_{i=1}^{n}\exp\left(-\frac{x_i – \mu}{\sigma}\right) $$
$$ \frac{\partial(\ln L)}{\partial \sigma} =-\frac{n}{\sigma} + \sum_{i=1}^{n}\frac{x_i – \mu}{\sigma^2} +\sum_{i=1}^{n}\frac{x_i – \mu}{\sigma^2}\exp\left(-\frac{x_i – \mu}{\sigma}\right) $$
となって、イコール $0$ とおいて整理すると
$$ \left\{\begin{split} \sigma &= \overline{x} – \frac{\sum_{i=1}^n x_i\exp\left(-\frac{x_i}{\sigma}\right)}{\sum_{i=1}^n \exp\left(-\frac{x_i}{\sigma}\right)}, \\ \mu &= -\sigma\ln\left[\frac{1}{n}\sum_{i=1}^{n}\exp\left(-\frac{x_i}{\sigma}\right)\right] \end{split}\right. $$
という連立方程式が得られます。これを解けば、$\mu$ と $\sigma$ の最尤推定量が得られます。
ここで、$\overline{x}$ は標本平均
$$ \overline{x} = \frac{1}{n}\sum_{i=1}^n x_i $$
です。
実装と実行
プログラムの例
与えられたヒストグラムに対して、グンベル分布、一般化極値分布、平方根指数型最大値分布を当てはめ、ヒストグラムに重ね書きするプログラムの例を示します。
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as ss
from scipy.optimize import minimize
#-----------------------------------------------------------------------------
# --- 平方根指数型最大値分布の関数
def sqet(x, a, b):
f = a*b*0.5*np.exp(-np.sqrt(b*x)-a*(1.0+np.sqrt(b*x))*np.exp(-np.sqrt(b*x)))
return f
def sqet_cdf(x, a, b):
F = np.exp(-a*(1.0+np.sqrt(b*x))*np.exp(-np.sqrt(b*x)))
return F
# SQETの対数尤度関数 (にマイナスをつけたもの)
def mL_sqet(b, data):
n = len(data)
sqbx = np.sqrt(b*data)
a = (np.sum(sqbx) -2.0*n) / np.sum(b*data*np.exp(-sqbx))
L = n*np.log(a) + n*np.log(b) -n*np.log(2) - np.sum(sqbx)
L = L - a*(np.sum(np.exp(-sqbx)) + np.sum(sqbx*np.exp(-sqbx)))
return -L
# bからaを求める式
def b2a_sqet(b, data):
n = len(data)
sqbx = np.sqrt(b*data)
a = (np.sum(sqbx) -2.0*n) / np.sum(b*data*np.exp(-sqbx))
return a
#------------------------------------------------------------------------------
# データの読み込み
year = []
annual_max_daily_prcp = []
i = 0
with open('data.csv', 'r') as fin:
for line in fin:
if i > 1:
data = line.split(',')
year.append(int(data[0]))
annual_max_daily_prcp.append(float(data[1].replace(']', '')))
i += 1
# ndarrayに変換
year = np.array(year)
annual_max_daily_prcp = np.array(annual_max_daily_prcp)
#------------------------------------------------------------------------------
# --- プロット
# 全般の設定
fig = plt.figure(figsize=(210/25.4, 294/25.4), dpi=100)
out_fig_path = 'histogram-and-fitted-pdf.png'
# プロット枠の設定
ax01 = fig.add_axes([0.10, 0.70, 0.80, 0.20])
ax02 = fig.add_axes([0.10, 0.40, 0.80, 0.20])
ax03 = fig.add_axes([0.10, 0.10, 0.80, 0.20])
# --- plot 1
# 年最大日降水量を西暦毎にバーグラフで表示
ax01.bar(year, annual_max_daily_prcp)
ax01.set_xlabel('year')
ax01.set_ylabel('annual maximum\\ndaily precipitation (mm)')
# グラフ上に最大値、最小値、平均値を表示
fig.text(0.01, 0.9, f'max: {annual_max_daily_prcp.max()} mm ({year[np.argmax(annual_max_daily_prcp)]})', transform=ax01.transAxes)
fig.text(0.01, 0.8, f'min: {annual_max_daily_prcp.min()} mm ({year[np.argmin(annual_max_daily_prcp)]})', transform=ax01.transAxes)
fig.text(0.01, 0.7, f'mean: {annual_max_daily_prcp.mean():.1f} mm', transform=ax01.transAxes)
# --- plot 2 と plot 3
# Gumbel分布を当てはめる
loc_gumbel, scale_gumbel = ss.gumbel_r.fit(annual_max_daily_prcp, method='MLE')
# 一般化極値分布を当てはめる
c_gev, loc_gev, scale_gev = ss.genextreme.fit(annual_max_daily_prcp, method='MLE')
# 平方根指数型最大値分布を当てはめる
res = minimize(mL_sqet, x0=[1.0], args=annual_max_daily_prcp,
bounds=[(0, None)], method='Nelder-Mead')
b_sqet = res.x[0]
a_sqet = b2a_sqet(b_sqet, annual_max_daily_prcp)
gbl = ss.gumbel_r(loc=loc_gumbel, scale=scale_gumbel)
gev = ss.genextreme(c=c_gev, loc=loc_gev, scale=scale_gev)
# bin, x のためのリストを作成する
bins = [10*(i+1) for i in range(int(annual_max_daily_prcp.max()/10) + 1)]
x = np.linspace(0.0, 10.0*(int(annual_max_daily_prcp.max()/10) + 1), 20*int(annual_max_daily_prcp.max()/10) + 1)
# ヒストグラムを表示
ax02.hist(annual_max_daily_prcp, bins=bins, density=True)
# 当てはめた分布をプロット
ax02.plot(x, gbl.pdf(x), label=f"scale={scale_gumbel:.2e}, loc={loc_gumbel:.2e}")
ax02.plot(x, gev.pdf(x), label=f"scale={scale_gev:.2e}, loc={loc_gev:.2e}, c={c_gev:.2e}")
ax02.plot(x, sqet(x, a_sqet, b_sqet), label=f"a={a_sqet:.2e}, b={b_sqet:.2e}")
ax02.legend()
# 累積ヒストグラムを表示
ax03.hist(annual_max_daily_prcp, bins=bins, cumulative=True, density=True)
ax03.plot(x, gbl.cdf(x))
ax03.plot(x, gev.cdf(x))
ax03.plot(x, sqet_cdf(x, a_sqet, b_sqet))
ax03.set_xlabel('annual maximum daily precipitation (mm)')
#------------------------------------------------------------------------------
# --- 図の保存
plt.savefig(out_fig_path, transparent=False)
このコードを fit-pdfs.pyとして、data.csv というデータファイルのあるディレクトリ (ここでは、~/Desktop/labcode/python/probable-precipitationとします。) に保存します。
データファイルは、二行目以降が第一コラムに年、第二コラムが年最大日降水量となっているものを想定しています。作り方は、以前の記事で紹介しています。参考にしてください。
プログラムを実行する
ターミナルを開き、
$ cd ~/Desktop/labcode/python/probable-precipitation
と入力し、ディレクトリを移動します( $マークは無視してください)。次のようにして先ほどのコードを実行しましょう。
$ python fit-pdfs.py
とします。histogram-and-fitted-pdf.png というファイルができて次のようになっていればひとまず成功です!
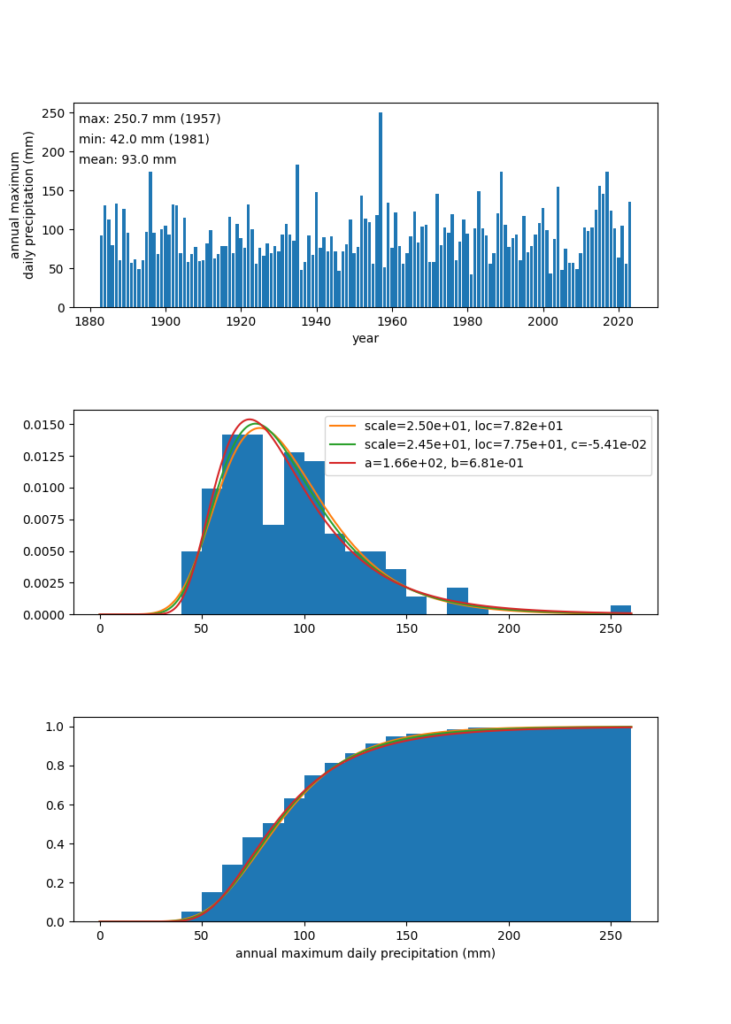
二段目の年最大日降水量のヒストグラムに橙色でグンベル分布、緑色で一般化極値分布、赤色で平方根指数型最大値分布を当てはめたものがプロットされ、右上にそれぞれのパラメータが表示されています。
コードの解説
上で紹介したコードの解説をします。
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as ss
from scipy.optimize import minimize
まず、必要なモジュールをインポートします。平方根指数型最大値分布の母数の最尤推定をするためにscipy.optimize から minimize をインポートしておきます。
#-----------------------------------------------------------------------------
# --- 平方根指数型最大値分布の関数
def sqet(x, a, b):
f = a*b*0.5*np.exp(-np.sqrt(b*x)-a*(1.0+np.sqrt(b*x))*np.exp(-np.sqrt(b*x)))
return f
def sqet_cdf(x, a, b):
F = np.exp(-a*(1.0+np.sqrt(b*x))*np.exp(-np.sqrt(b*x)))
return F
# SQETの対数尤度関数 (にマイナスをつけたもの)
def mL_sqet(b, data):
n = len(data)
sqbx = np.sqrt(b*data)
a = (np.sum(sqbx) -2.0*n) / np.sum(b*data*np.exp(-sqbx))
L = n*np.log(a) + n*np.log(b) -n*np.log(2) - np.sum(sqbx)
L = L - a*(np.sum(np.exp(-sqbx)) + np.sum(sqbx*np.exp(-sqbx)))
return -L
# bからaを求める式
def b2a_sqet(b, data):
n = len(data)
sqbx = np.sqrt(b*data)
a = (np.sum(sqbx) -2.0*n) / np.sum(b*data*np.exp(-sqbx))
return a
平方根指数型最大値分布の確率密度関数、累積分布関数を定義し、さらに最尤法に必要になる対数尤度関数を定義しておきます。式の導出等は下の補遺に書いておきましたので、興味のある方は参照してください。
最後のものは、$b$と$a$の関係式で、$b$を求めた後、$a$を求める式です。
#------------------------------------------------------------------------------
# データの読み込み
year = []
annual_max_daily_prcp = []
i = 0
with open('data.csv', 'r') as fin:
for line in fin:
if i > 1:
data = line.split(',')
year.append(int(data[0]))
annual_max_daily_prcp.append(float(data[1].replace(']', '')))
i += 1
# ndarrayに変換
year = np.array(year)
annual_max_daily_prcp = np.array(annual_max_daily_prcp)
この部分は、年最大日降水量のデータを読み込んでいる部分です。このデータの用意の仕方は、以前紹介しましたので、そちらを参照してください。
#------------------------------------------------------------------------------
# --- プロット
# 全般の設定
fig = plt.figure(figsize=(210/25.4, 294/25.4), dpi=100)
out_fig_path = 'histogram-and-fitted-pdf.png'
# プロット枠の設定
ax01 = fig.add_axes([0.10, 0.70, 0.80, 0.20])
ax02 = fig.add_axes([0.10, 0.40, 0.80, 0.20])
ax03 = fig.add_axes([0.10, 0.10, 0.80, 0.20])
# --- plot 1
# 年最大日降水量を西暦毎にバーグラフで表示
ax01.bar(year, annual_max_daily_prcp)
ax01.set_xlabel('year')
ax01.set_ylabel('annual maximum\\ndaily precipitation (mm)')
# グラフ上に最大値、最小値、平均値を表示
fig.text(0.01, 0.9, f'max: {annual_max_daily_prcp.max()} mm ({year[np.argmax(annual_max_daily_prcp)]})', transform=ax01.transAxes)
fig.text(0.01, 0.8, f'min: {annual_max_daily_prcp.min()} mm ({year[np.argmin(annual_max_daily_prcp)]})', transform=ax01.transAxes)
fig.text(0.01, 0.7, f'mean: {annual_max_daily_prcp.mean():.1f} mm', transform=ax01.transAxes)
ファイル名や、プロットする枠を設定しています。
その後、年最大日降水量を西暦毎にバーグラフで表示しています。
# --- plot 2 と plot 3
# Gumbel分布を当てはめる
loc_gumbel, scale_gumbel = ss.gumbel_r.fit(annual_max_daily_prcp, method='MLE')
# 一般化極値分布を当てはめる
c_gev, loc_gev, scale_gev = ss.genextreme.fit(annual_max_daily_prcp, method='MLE')
# 平方根指数型最大値分布を当てはめる
res = minimize(mL_sqet, x0=[1.0], args=annual_max_daily_prcp,
bounds=[(0, None)], method='Nelder-Mead')
b_sqet = res.x[0]
a_sqet = b2a_sqet(b_sqet, annual_max_daily_prcp)
ここは、二番目と三番目のプロットや分布関数の当てはめに関する部分です。
分布関数を当てはめるには、ss.gumbel_r.fit(annual_max_daily_prcp) のようにして、引数に当てはめたい分布の元となるデータを渡します。method には、母数推定法を与えます。MLE は 最尤法 (most likelihood estimation) です。デフォルトはMLEなので与えなくてもOKです。
平方根指数型最大値分布に関しては、上の方で定義した mL_sqet を最小化するように選びます。筆者は scipy.optimize の [minimize](<https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html>) を利用しました。 戻り値の .x で解 (のアレイ) が得られます。ここでは、$b$ の値です。$b$ が得られましたので、b2a_sqet に渡して、$a$ を得ます。
gbl = ss.gumbel_r(loc=loc_gumbel, scale=scale_gumbel)
gev = ss.genextreme(c=c_gev, loc=loc_gev, scale=scale_gev)
# bin, x のためのリストを作成する
bins = [10*(i+1) for i in range(int(annual_max_daily_prcp.max()/10) + 1)]
x = np.linspace(0.0, 10.0*(int(annual_max_daily_prcp.max()/10) + 1), 20*int(annual_max_daily_prcp.max()/10) + 1)
# ヒストグラムを表示
ax02.hist(annual_max_daily_prcp, bins=bins, density=True)
# 当てはめた分布をプロット
ax02.plot(x, gbl.pdf(x), label=f"scale={scale_gumbel:.2e}, loc={loc_gumbel:.2e}")
ax02.plot(x, gev.pdf(x), label=f"scale={scale_gev:.2e}, loc={loc_gev:.2e}, c={c_gev:.2e}")
ax02.plot(x, sqet(x, a_sqet, b_sqet), label=f"a={a_sqet:.2e}, b={b_sqet:.2e}")
ax02.legend()
# 累積ヒストグラムを表示
ax03.hist(annual_max_daily_prcp, bins=bins, cumulative=True, density=True)
ax03.plot(x, gbl.cdf(x))
ax03.plot(x, gev.cdf(x))
ax03.plot(x, sqet_cdf(x, a_sqet, b_sqet))
ax03.set_xlabel('annual maximum daily precipitation (mm)')
ここからは、先ほど求めたパラメータを使って、プロットを進めていく部分です。
gbl = ss.gumbel_r(loc=loc_gumbel, scale=scale_gumbel) 等で関数のインスタンスを作って、gbl.pdf で確率密度関数が、gbl.cdf で累積分布関数がプロットできます。
平方根指数型最大値分布については、上で用意した関数を使って、sqrt と sqrt_cdf でプロットしています。
最後に
今回は、「〇〇年に一度の大雨」について理解するために、年最大日降水量のヒストグラムに分布関数を当てはめる方法 (最尤法) を紹介しました。実際に当てはめを体験すると、教科書で目にする若干無味乾燥な最尤法が、生きたものとして実感できるのではないでしょうか。
次回は当てはまり具合の指標や、当てはめた関数を使って確率降水量の値を実際に算出してみます。
補遺
平方根指数型最大値分布の母数の最尤推定法
平方根指数型最大値分布 (前回の記事も参照) は
$$ f(x) = \frac{ab}{2}\exp\left[-\sqrt{bx} – a\left(1+\sqrt{bx}\right)\exp\left(-\sqrt{bx}\right)\right] $$
でした。この対数尤度関数は
$$ \ln L(a, b) = n\ln a + n\ln b – n\ln 2 +\sum_{i=1}^{n}\left[-\sqrt{bx_i} – a(1+\sqrt{bx_i})\exp(-\sqrt{bx_i})\right] $$
となります。これを $a$ と $b$ でそれぞれ偏微分すると
$$ \frac{\partial (\ln L)}{\partial a} = \frac{n}{a} – \sum_{i=1}^n(1+\sqrt{bx_i})\exp(-\sqrt{bx_i}) $$
$$ \frac{\partial (\ln L)}{\partial b} = \frac{n}{b} – \sum_{i=1}^n\left[ \frac{1}{2}\sqrt{\frac{x_i}{b}} -\frac{a}{2}x_i\exp(-\sqrt{bx_i})\right] $$
となるので、それぞれ0とおいて整理すると
$$ \left\{\begin{split} a &= \frac{n}{\sum_{i=1}^n (1+\sqrt{bx_i})\exp(-\sqrt{bx_i})}, \\ a &= \frac{\sum_{i=1}^n \sqrt{bx_i} – 2n}{\sum_{i=1}^n bx_i\exp(-\sqrt{bx_i})} \end{split}\right. $$
という連立方程式が得られます。これを解くには scipy.optimize 等に用意されている方法を使うことができます。
参考文献
本記事を執筆するに当たり、次の資料・文献を参考にしました。
- 気象庁、確率降水量の推定方法:https://www.data.jma.go.jp/cpdinfo/riskmap/cal_qt.html
- 椎葉充晴、立川康人、市川温、『例題で学ぶ水文学』、森北出版
- M. Evans, N. Hastings, B. Peacock, “Statistical Distributions, Third Edition”, Wiley-Interscience.
- 星清、『水文統計解析』、開発土木研究月報 No.540、1998年5月:https://thesis.ceri.go.jp/db/files/0005005050.pdf
Pythonでやってみる気象データ解析の技術書を販売中
¥2,500 → ¥1,500 今なら40%OFF!!
気象の勉強をされている方必読!
気象予報士でもある著者がわかりやすく解説
プログラムを公開しているのでお手元で試せます!




