Numerical Solutions to Two-Dimensional Parabolic Partial Differential Equations with Code [Python]

In this article, we will delve into the numerical solutions of two-dimensional parabolic partial differential equations, with easy-to-understand concrete examples. We will learn an approach using Python.

Through this article, let’s master one of the numerical solutions for partial differential equations!

Note: The discussion is limited to the finite difference method. Details on errors and boundary conditions are omitted to avoid redundancy.

What is Numerical Solution of Partial Differential Equations?

The numerical solution of partial differential equations (PDEs) refers to methods used to approximate the solutions of PDEs. Since analytical solutions are often not possible, numerical methods become necessary. Below, we introduce several main numerical methods.

1. Finite Difference Method: This method discretizes space and time into a grid and approximates derivatives with differences. While intuitive and relatively easy to implement, the choice of grid significantly affects the solution’s accuracy.

2. Finite Element Method: The problem domain is divided into small “elements,” and equations are approximated within each element. This method is suitable for problems with complex shapes or boundary conditions.

3. Finite Volume Method: Particularly suited for conservation law equations, the domain is divided into small “volumes,” and average values within each volume are calculated.

4. Spectral Method: The equation is represented as a sum of waves with different frequencies, and solving involves calculating the coefficients of these waveforms. High accuracy can be achieved, but smooth solutions are required.

5. Finite-Difference Time-Domain (FDTD) Method: A type of finite difference method used extensively in electromagnetics, applied in the time domain.

These methods are used in physics, engineering, meteorology, and other fields to solve PDEs. Each method has its characteristics and applicable problem types, so choosing the optimal method according to the problem’s nature is necessary. In advanced computer simulations, these methods are often combined.

This article introduces the Finite Difference Method for numerical solutions.

Difference Approximation

In the numerical solution of partial differential equations, the finite difference method is very commonly used.

The finite difference method utilizes difference approximations. The details of the concept of difference approximation for partial derivatives are covered in another article, and here we will briefly introduce only the difference approximation used for parabolic equations, which is the main topic of this article.

Let $u = u(x,y)$ be given in the domain $0 \leqq x \leqq a, 0 \leqq y \leqq b$. Divide this domain into a grid (difference grid) as shown below. The grid spacing can be equal or, as shown in the figure, unequal.

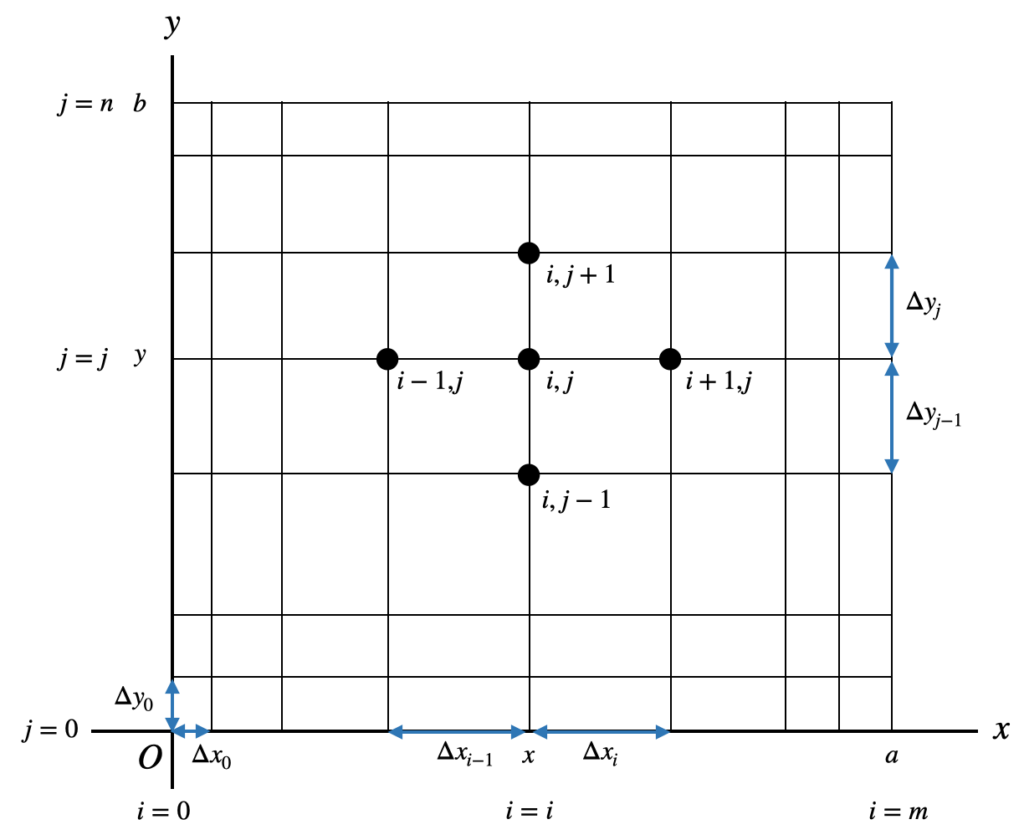
Label the grid points in the $x$ direction as $i=0 \sim m$ and in the $y$ direction as $j=0 \sim n$. Label the point $(x,y)$ on the grid as $(i,j)$ and the value of $u$ at this point as $u_{i,j}$. Label the neighboring grid points as shown in the figure with $\Delta x_i,\Delta y_i$, etc. The difference approximations for partial derivatives $∂u/∂x, ∂u/∂y$ can be represented as follows, fixing $j$ for $∂u/∂x$ and $i$ for $∂u/∂y$.

When the grid spacing is uniform,

$$
\begin{aligned}
\Delta x_{i-1} &= \Delta x_{i} =h \\
\Delta y_{i-1} &= \Delta y_{i} =k \end{aligned}
$$

thus, the first-order partial derivative coefficients are obtained using the forward difference approximation as follows:

$$
\begin{aligned}
\frac{∂u}{∂x} &= \frac{1}{h}(u_{i+1,j} – u_{i,j}) \\
\frac{∂u}{∂y} &= \frac{1}{k}(u_{i,j+1} – u_{i,j})
\end{aligned}
$$

Furthermore, the second-order partial derivative coefficients are obtained using the central difference approximation as follows:

$$
\begin{align*}
\frac{∂^2u}{∂x∂y} &= \frac{1}{4hk}(u_{i+1,j+1} – u_{i+1,j-1} – u_{i-1,j+1} + u_{i-1,j-1}) \\
\frac{∂^2u}{∂x^2} &= \frac{1}{h^2}(u_{i+1,j} – 2u_{i,j} + u_{i-1,j}) \\
\frac{∂^2u}{∂y^2} &= \frac{1}{k^2}(u_{i,j+1} – 2u_{i,j} + u_{i,j-1})
\end{align*}
$$

These difference approximations are used to convert partial differential equations into difference equations.

Overview of Numerical Solution using the Finite Difference Method

The steps for numerically solving a partial differential equation using the finite difference method are:

1. Convert the partial differential equation into a difference equation.

2. Calculate the values of each element using the difference equation.

Let’s explain each step below.

Converting Partial Differential Equations to Difference Equations

Consider solving two-dimensional parabolic equations as an example:

$$
\frac{∂u}{∂t} = \chi \Big( \frac{∂^2u}{∂x^2} + \frac{∂^2u}{∂y^2} \Big); \ \ \ \ \ \ 0 \leqq x \leqq a, 0 \leqq y \leqq b, 0 \leqq t < \infty \ \ \ \ (1)
$$

Initial condition: $u(x,y,0)= f(x,y)$

Boundary conditions:
$u(0,y,t) = g_1(y,t), \ \ \ u(a,y,t) = g_2(y,t)$
$u(x,0,t) = g_3(x,t), \ \ \ u(x,b,t) = g_4(x,t)$

Let’s consider solving under these conditions as an example.

Here, $t$ represents time, and $\chi$ represents the thermal conductivity, which is considered a constant. ($\chi, a, b, g_1(y,t), g_2(y,t), g_3(x,t), g_4(x,t)$ are known.)

First, let’s express equation $(1)$ as a difference equation. Thus, $x, y, t$ will be as follows:

$$
t = k \Delta t, \ \ \ x = i \Delta x, \ \ \ y = j \Delta y
$$

The conversion to a difference equation reuses the finite difference approximations of the partial derivatives. Namely,

$$
\frac{(u_{i,j,k+1} – u_{i,j,k}) }{\Delta t} = \chi \left\{ \frac{(u_{i+1,j,k} – 2u_{i,j,k} + u_{i-1,j,k}) }{(\Delta x)^2} + \frac{(u_{i,j+1,k} – 2u_{i,j,k} + u_{i,j-1,k}) }{(\Delta y)^2} \right\}
$$

Rearranging this equation for $u_{i,j,k+1}$ yields

$$
u_{i,j,k+1} = u_{i,j,k} + \Delta t \chi \left\{ \frac{u_{i+1,j,k} – 2u_{i,j,k} + u_{i-1,j,k} }{(\Delta x)^2} + \frac{u_{i,j+1,k} – 2u_{i,j,k} + u_{i,j-1,k}}{(\Delta y)^2} \right\} \ \ \ \ \ (2)
$$

Calculating the Values of Each Element Using Difference Equations

Looking closely at difference equation $(2)$,

If we set $k=0,1,2, …, l-1$, the value of $u_{i,j}$ at $k=0$ is known from the initial and boundary conditions, so the values of $u_{i,j}$ at subsequent times can be determined in sequence.

This method of directly obtaining the values of $u$ at the next time step from the known values at the current time step is known as the explicit method.

Furthermore, let’s rearrange difference equation $(2)$ as follows:

$$
u_{i,j,k+1} = \Delta t \chi \left\{ \frac{u_{i+1,j,k} + u_{i-1,j,k} }{(\Delta x)^2} + \frac{u_{i,j+1,k} + u_{i,j-1,k}}{(\Delta y)^2} \right\} + \left\{ 1 – 2 \Delta t \chi \left( \frac{1}{(\Delta x)^2} + \frac{1}{(\Delta y)^2} \right) \right\} u_{i,j,k} \ \ \ \ \ (3)
$$

Assuming that temperature always takes on positive values, the first term on the right side of equation $(3)$ will be positive, and the second term will have the following condition:

$$
1 – 2 \Delta t \chi \left( \frac{1}{(\Delta x)^2} + \frac{1}{(\Delta y)^2} \right) \geq 0
$$

$$
\therefore \Delta t \chi \left( \frac{1}{(\Delta x)^2} + \frac{1}{(\Delta y)^2} \right) \leq \frac{1}{2} \ \ \ \ (4)
$$

The explicit method is simple and easy to understand, but as indicated by condition $(4)$, it requires $\Delta t$ to be very small relative to $\Delta x$ and $\Delta y$, which can significantly increase computation time. An effective method to overcome this inconvenience is the Crank-Nicolson implicit method.
We will introduce the implicit method in another article, if there’s an opportunity.

Example Problem

Investigate how the temperature distribution inside a square plate (with side length $1$ $\mathrm{m}$), initially at $0$ ℃, changes over time when three sides are kept at $u=0$ and the side at $y=1$ is maintained at $u=4x(1-x)$. The thermal conductivity of the plate is $\chi = 0.07$ $\mathrm{m^2/h}$.

The fundamental equation and conditions for the temperature distribution $u(x, y,t)$ are as follows:

$$
\frac{\partial u}{\partial t} = \chi \left( \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} \right); \ \ \ \ \ \ 0 \leq x \leq 1, 0 \leq y \leq 1, 0 \leq t < \infty \ \ \ \ (1)
$$

Initial condition: $u(x,y,0)= 0$

Boundary conditions:

$u(0,y,t) = 0, \ \ \ u(1,y,t) = 0$
$u(x,0,t) = 0, \ \ \ u(x,1,t) = 4x(1-x)$

Let the grid numbers be $i=0 \sim m, j=0 \sim n, k=0 \sim l$, and denote the value of $u$ at any grid point as $u_{i,j,k}$.

As introduced earlier, let’s first convert this partial differential equation into a difference equation, and then implement a program to solve the difference equation.

Implementation Method

The code can be implemented as follows:

The creation of graphs and output to text files is also included, making the code somewhat lengthy, but the crucial part is the calculate_equation function.

Save the following implementation as main.py in a folder (here, ~/Desktop/labcode/python/numerical_calculation/2d_parabolic_equation).

import matplotlib.pyplot as plt
from matplotlib.animation import ArtistAnimation
import numpy as np


def _set_initial_condition(
    *,
    array_3d: list,
    grid_counts_x: int,
    grid_counts_y: int,
) -> None:
    """
    Set initial condition

    Set all U values except for boundaries to 0.0
    """
    for i in range(1, grid_counts_x):
        for j in range(1, grid_counts_y):
            array_3d[0][i][j] = 0.0


def _set_boundary_condition(
    *,
    array_3d: list,
    grid_counts_x: int,
    grid_counts_y: int,
    grid_counts_t: int,
    grid_space_x: float,
) -> None:
    """Set boundary conditions"""
    for k in range(grid_counts_t + 1):
        for i in range(grid_counts_x + 1):
            array_3d[k][i][0] = 0.0
            array_3d[k][i][grid_counts_y] = (
                4 * i * grid_counts_x * (1.0 - i * grid_space_x)
            )

        for j in range(grid_counts_y + 1):
            array_3d[k][0][j] = 0.0
            array_3d[k][grid_counts_x][j] = 0.0


def calculate_equation(
    *,
    M: int,
    N: int,
    L: int,
    DX: float,
    DY: float,
    DT: float,
    CHI: float,
) -> list:
    """
    Calculate the difference equation

    The core function of this program
    """
    # List for U values
    U: list = [
        [[0.0 for _ in range(N + 1)] for _ in range(M + 1)] for _ in range(L + 1)
    ]

    # Set initial values
    _set_initial_condition(
        array_3d=U,
        grid_counts_x=M,
        grid_counts_y=N,
    )
    _set_boundary_condition(
        array_3d=U,
        grid_counts_x=M,
        grid_counts_y=N,
        grid_counts_t=L,
        grid_space_x=DX,
    )

    # Calculation
    for k in range(L):
        for j in range(1, N):
            for i in range(1, M):
                A = (U[k][i + 1][j] - 2 * U[k][i][j] + U[k][i - 1][j]) / (DX**2)
                B = (U[k][i][j + 1] - 2 * U[k][i][j] + U[k][i][j - 1]) / (DY**2)
                U[k + 1][i][j] = U[k][i][j] + CHI * DT * (A + B)
    return U


def animate_time_evolution(
    *,
    array_3d: list,
    grid_counts_x: int,
    grid_counts_y: int,
    grid_counts_t: int,
    grid_space_x: float,
    grid_space_y: float,
    time_delta: float,
) -> None:
    """
    Create animation
    Plot data from array_3d and display time evolution as an animation
    """

    # Create animation
    fig, ax = plt.subplots(figsize=(5, 5))
    extent = [
        0 - grid_space_x * 0.5,
        grid_counts_x * grid_space_x + grid_space_x * 0.5,
        0 - grid_space_y * 0.5,
        grid_counts_y * grid_space_y + grid_space_y * 0.5,
    ]
    plt.xlabel("X (m)")
    plt.ylabel("Y (m)")
    path_gif = "./animation.gif"

    frames = []
    for k in range(grid_counts_t + 1):
        U_2dim = [
            [0.0 for _ in range(grid_counts_x + 1)] for _ in range(grid_counts_y + 1)
        ]
        for j in range(grid_counts_y + 1):
            for i in range(grid_counts_x + 1):
                U_2dim[i][j] = array_3d[k][i][j]

        frame = plt.imshow(
            np.array(U_2dim).T,
            cmap="viridis",
            interpolation="none",
            aspect="auto",
            origin="lower",
            extent=extent,
        )
        time = k * time_delta
        text = ax.text(
            0.05,
            1.05,
            f"t = {time:.2f} (h)",
            transform=ax.transAxes,
            fontsize=14,
            verticalalignment="top",
        )
        frames.append([frame] + [text])

    anim = ArtistAnimation(fig, frames, interval=100)
    anim.save(path_gif, writer="pillow")


def output_result_file(
    *,
    array_3d: list,
    grid_counts_x: int,
    grid_counts_y: int,
    grid_counts_t: int,
    grid_space_x: float,
    grid_space_y: float,
    time_delta: float,
) -> None:
    """Write 2D array to a text file"""
    with open("./calculated_result.txt", "w") as file:
        file.write(f"# This file shows calculated result as below.\n\n")
        file.write(f"# Calculation Parameters.\n")
        file.write(f"grid_counts_x: {grid_counts_x}\n")
        file.write(f"grid_counts_y: {grid_counts_y}\n")
        file.write(f"grid_counts_t: {grid_counts_t}\n")
        file.write(f"grid_space_x: {grid_space_x}\n")
        file.write(f"grid_space_y: {grid_space_y}\n")
        file.write(f"time_delta: {time_delta}\n\n")

        file.write(f"# Calculated Matrix U at the each time.\n")
        for k in range(grid_counts_t + 1):
            file.write(f"time = {time_delta * k} h\n")

            for row in array_3d[k]:
                line = " ".join(map(str, row))
                file.write(line + "\n")
            file.write("\n")


def validate_parameters(R: float) -> None:
    """Check the validity of parameters"""
    if R > 0.5:
        raise ValueError("R must be less than 0.5.")


if __name__ == "__main__":
    """
    Numerical solution of two-dimensional parabolic equations (explicit method)
    """
    grid_counts_x: int = 10  # Number of grid points
    grid_counts_y: int = 10  # Number of grid points
    grid_counts_t: int = 500  # Number of grid points
    grid_space_x: float = 0.1  # Grid spacing (m)
    grid_space_y: float = 0.1  # Grid spacing (m)
    time_delta: float = 0.02  # Time step (h)
    CHI: float = 0.07  # Thermal conductivity (m^2/h)
    r: float = CHI * (1 / grid_space_x**2 + 1 / grid_space_y**2) * time_delta

    validate_parameters(R=r)

    array_3d = calculate_equation(
        M=grid_counts_x,
        N=grid_counts_y,
        L=grid_counts_t,
        DX=grid_space_x,
        DY=grid_space_y,
        DT=time_delta,
        CHI=CHI,
    )
    animate_time_evolution(
        array_3d=array_3d,
        grid_counts_x=grid_counts_x,
        grid_counts_y=grid_counts_y,
        grid_counts_t=grid_counts_t,
        grid_space_x=grid_space_x,
        grid_space_y=grid_space_y,
        time_delta=time_delta,
    )
    output_result_file(
        array_3d=array_3d,
        grid_counts_x=grid_counts_x,
        grid_counts_y=grid_counts_y,
        grid_counts_t=grid_counts_t,
        grid_space_x=grid_space_x,
        grid_space_y=grid_space_y,
        time_delta=time_delta,
    )

Executing the Program

Open the terminal and enter:

$ cd Desktop/labcode/python/numerical_calculation/2d_parabolic_equation

Then, execute the following command (ignore the $ symbol):

$ python main.py

Execution Results

If a file named animation.gif has been created in ~/Desktop/LabCode/python/numerical_calculation/2d_parabolic_equation and it turns into a gif image like the following, then it’s a success!

The temperature at the right boundary at $t=5.5$ is gradually spreading upwards, as visualized.
By $t=5.5$ $\mathrm{h}$, it is also evident that it has almost reached thermal equilibrium.

Additionally, a text file named calculated_result.txt should have been created as follows. Although only basic information is outputted this time, by outputting the calculation results along with the parameters used for the calculation, it becomes possible for others to evaluate the results. For your own benefit as well as for the benefit of others, make it a habit to output the results.

# This file shows calculated result as below.

# Calculation Parameters.
grid_counts_x: 10
grid_counts_y: 10
grid_counts_t: 500
grid_space_x: 0.1
grid_space_y: 0.1
time_delta: 0.02

# Calculated Matrix U at the each time.
time = 0.0 h
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 36.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 64.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 84.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 96.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 100.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 95.99999999999997
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 83.99999999999999
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 63.999999999999986
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 35.99999999999999
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0

...

In Conclusion

We have introduced the numerical solution of two-dimensional parabolic partial differential equations using the finite difference method.

The Python computation program is also generously shared, so please deepen your understanding by running it.

In the future, we will write new articles on numerically solving other types of partial differential equations, so we hope you will look forward to them.