【MetPy】Calculate atmospheric stability index from vertical profile【Weather Data】

Introduction

In a previous article, we introduced that the stability of the atmosphere can be understood by looking into the emagram.

Some quantitative indices determined from the vertical distribution of temperature and humidity have been proposed, and these indices can be used to estimate atmospheric stability and the possibility of thunderstorms.

In this article, we will explain the definition of these indices and how to calculate them using MetPy.

Tested Environment

macOS Monterey 12.6.2, Python 3.9.15, MetPy 1.3.1

Stability Indices related to Vertical Profile

LCL (Lifted Condensation Level)

This is the altitude at which condensation occurs when the air parcel near the ground is lifted. In the emagram, this is the point where the dry adiabatic line that passes through the air temperature near the ground and the isosaturated mixing ratio line that passes through the dew point temperature intersect.

In MetPy, you can calculate withmetpy.calc.lcl(pressure, temperature, dewpoint, max_iters=50, eps=1e-05).

LFC (Level of Free Convection)

This is the altitude at which the temperature of the air parcel near the ground becomes higher than the surrounding air temperature when the air mass is lifted up.

Above the LFC, air parcels gain buoyancy and can rise without external force. Low LFC means that more convective activity occurs.

In MetPy, you can calculate with metpy.calc.lfc(pressure, temperature, dewpoint, parcel_temperature_profile=None, dewpoint_start=None, which='top').

EL (Equilibrium Level)

This is the altitude at which the buoyant force becomes 0 above the free convection altitude when air parcels near the ground are lifted adiabatically. There may be multiple altitude candidates, but choose one as the highest altitude or (more on that later) the altitude that maximizes CAPE. This altitude is a guide to the height of convective clouds.

In MetPy, you can calculate withmetpy.calc.el(pressure, temperature, dewpoint, parcel_temperature_profile=None, which='top').

CIN (Convective Inhibition)

Convective INhibition is expressed by the area in the figure below. It represents the energy required to raise a mass of air near the earth’s surface to a free convection altitude. It is defined as:

$$ \text{CIN} = -g\int_{z_0}^{\text{LFC}}\frac{T(z) – \overline{T(z)}}{\overline{T(z)}}\mathrm{d}z, $$

where $T(z)$ varies along the dry adiabatic lapse rate until the air parcel is saturated and then varies along the wet adiabatic lapse rate after saturation. $\overline{T(z)}$ is the temperature of the “surrounding” air represented by the state curve.

If we assume hydrostatic $\mathrm{d}p = -\rho g\mathrm{d}z$ and using equation of state $p = \rho R T$, we yield

$$ \mathrm{d}(\ln p) = \frac{\mathrm{d}p}{p} = -\frac{g\mathrm{d}z}{RT} $$

Thus, the above definition of CIN can be reduced to

$$ \text{CIN} = R\int_{p_0}^{\text{LFC}} (T(p) – \overline{T(p)})\mathrm{d}(\ln p) $$

By this formula, we can get CIN from pressure-temperature data.

Small CIN means that convection is likely.

CAPE (Convective Available Potential Energy)

Convective Available potential energy is expressed by the area in the diagram below. Above the free convection altitude, air parcels experience buoyancy and can gain energy. It represents the magnitude of this energy and is defined as

$$ \text{CAPE} = g \int_{\text{LFC}}^{\text{EL}}\frac{T(z) – \overline{T(z)}}{\overline{T(z)}}\mathrm{d}z $$

By the same procedure as CIN, we can write

$$ \text{CAPE} = -R \int_{\text{LFC}}^{\text{EL}}(T(p) – \overline{T(p)})\mathrm{d}(\ln p) $$

If this value is large, it can be said that the atmospheric condition is unstable. In 「シビア現象の監視・予測について」(2021年3月) (in Japanese), atmospheric stability is classified in general as follows

CAPE (J/kg)	atmospheric stability
0 or less	stable
0 to 1000	weak instability
1000 to 2500	moderate instability
2500 to 3500	strong instability
above 3500	extreme instability

In MetPy, we can calculate CIN and CAPE withmetpy.calc.surface_based_cape_cin(pressure, temperature, dewpoint). (REMARK: The definition of CIN in MetPy has an opposite sign.)

SSI (Shawalter Stability Index)

SSI is a subtraction from 500 hPa temperature $T_{500}$ to the temperature when the air parcel at 850 hPa is lifted $T_{850\to 500}$.

The rules for lifting air parcels are the same: they are lifted along the dry adiabatic line until they reach saturation and then along the wet adiabatic line after saturation.

$$ \text{SSI} = T_{500} – T_{850\to 500} $$

If the SSI is negative, it means that when lifting an air parcel at 850 hPa, the temperature is higher than the temperature at 500 hPa, so the atmospheric conditions are unstable. In 「シビア現象の監視・予測について」(2021年3月) (in Japanese), atmospheric stability is classified in general as follows

SSI (℃)	atmospheric stability
above 0	stable
0 to -3	weak instability (possible thunderstorms)
-3 to -6	moderate instability (possible severe convective activity)
-6 to -9	strong instability
below -9	extreme instability

In MetPy, you can calculate with metpy.calc.showalter_index(pressure, temperature, dewpoint) .

KI (K-index)

KI is defined as follows:

$$ K\text{-index} = (T_{850} – T_{500}) + T_\text{d, 850} – (T_{700} – T_\text{d, 700}), $$

where $T_{\text{d, 850}}$ and $T_{\text{d, 700}}$ are the dew points at 850 hPa and 700 hPa.

The more the KI is, the more likely a thunderstorm will occur. In 「シビア現象の監視・予測について」(2021年3月) (in Japanese), the general relation of KI and the probability of thunderstorms is explained as follows.

KI (℃)	probability of thunderstorms
less than 15	none
15 to 20	20％
21 to 25	20 to 40%
26 to 30	40 to 60%
31 to 35	60 to 80％
36 to 40	80 to 90%
more than 40	almost 100%

In MetPy, you can calculate withmetpy.calc.k_index(pressure, temperature, dewpoint, vertical_dim=0) .

Implementation Example

First, we have to prepare upper-air meteorological observation data.

We have prepared a dataset that includes atmospheric pressure, temperature, and humidity. Please download and use it. The first line contains the barometric pressure, the second line contains the temperature, and the third line contains the relative humidity.

20170705_09JST_47807.txt

Let’s calculate the metrics mentioned above and display them above the emgram. An example implementation is shown below. Copy the code below and save it as plot-emagram-and-calc-params.pyin an appropriate directory (say ~/Desktop/labcode/python/plot-emagram-and-calc-params). Make sure to put the data files shown above in the same directory.

import matplotlib.pyplot as plt
import metpy.calc as mpcalc
from metpy.plots import SkewT
from metpy.units import units
import numpy as np

#------------------------------------------------------------------------------
# read data
fname = "20170705_09JST_47807.txt"
data = np.genfromtxt(fname=fname, unpack=True)

prss_pcl = 950 * units.hPa # pressure surface where parcel located

prss = data[0]*units.hPa # pressure
tmpr = data[1]*units.degC # temperature
rhmd = data[2] # relative humidity

#------------------------------------------------------------------------------
# --- calculation
# dew point
dewp = mpcalc.dewpoint_from_relative_humidity(tmpr, rhmd/100.0)

# get index of the pressure where parcel located
i_prss_pcl = np.argmin(np.abs(prss_pcl.magnitude - prss.magnitude))

# calculate temperature evolution
prss_wlcl, tmpr_wlcl, dewp_wlcl, prof_wlcl = mpcalc.parcel_profile_with_lcl(prss[i_prss_pcl:], tmpr[i_prss_pcl:], dewp[i_prss_pcl:])

# LCL (Lifted Condensation Level)
lcl_prss, lcl_tmpr = mpcalc.lcl(prss[i_prss_pcl], tmpr[i_prss_pcl], dewp[i_prss_pcl])

# LFC (Level of Free Convection) 
lfc_prss, lfc_tmpr = mpcalc.lfc(prss[i_prss_pcl:], tmpr[i_prss_pcl:], dewp[i_prss_pcl:])

# EL (Equilibrium Level)
el_prss, el_tmpr = mpcalc.el(prss, tmpr, dewp)

# CAPE (convective available potential energy) and 
# CIN (convective inhibition)
cape, cin = mpcalc.surface_based_cape_cin(prss, tmpr, dewp)

# SSI (Shawalter Stability Index)
ssi = mpcalc.showalter_index(prss, tmpr, dewp)

# KI (K-index)
ki = mpcalc.k_index(prss, tmpr, dewp)

#------------------------------------------------------------------------------
# *** plot
# --- plot area
xmax = 40 # 
xmin = -90 # 
ymin = 100 # 
ymax = 1020 # 

# --- overall setting
fig = plt.figure(figsize=(210/25.4, 294/25.4), dpi=100)
out_fig_path = 'emagram.png'

# --- write comments
fig.text(0.05, 0.95, f"starting parcel pressure = {prss[i_prss_pcl].magnitude:.0f} hPa")
fig.text(0.05, 0.93, f"LCL = {lcl_prss.magnitude:.0f} hPa")
fig.text(0.05, 0.91, f"LFC = {lfc_prss.magnitude:.0f} hPa")
fig.text(0.05, 0.89, f"EL = {el_prss.magnitude:.0f} hPa")

fig.text(0.55, 0.95, f"CIN = {cin.magnitude:.0f} J/kg")
fig.text(0.55, 0.93, f"CAPE = {cape.magnitude:.0f} J/kg")
fig.text(0.55, 0.91, f"SSI = {ssi[0].magnitude:.0f}℃")
fig.text(0.55, 0.89, f"KI = {int(ki.magnitude):.0f}℃")

# --- skew T diagram 
skew = SkewT(fig, rotation=0, aspect=150)

# --- axis
skew.ax.set_xlim(xmin, xmax)
skew.ax.set_ylim(ymax, ymin)

# --- label
skew.ax.set_xlabel('Temperature (℃)')
skew.ax.set_ylabel('Pressure (hPa)')

# --- temperature, dewpoint, and wind profiles
skew.plot(prss, tmpr, 'red')
skew.plot(prss, dewp, 'blue')
skew.plot(prss_wlcl, prof_wlcl, 'black')

# --- LCL, LFC and EL
skew.plot(lcl_prss, lcl_tmpr, 'ko', markerfacecolor='black')
skew.plot(lfc_prss, lfc_tmpr, 'ko', markerfacecolor='black')

# --- dry adiabatic 
t0 = np.arange(200, 360, 10)*units.K # starting points

# plot
skew.plot_dry_adiabats(t0=t0, lw=0.5, colors='red')

# put labels at 350hPa
for t in t0:
    p1 = 350*units.hPa
    t1 = mpcalc.dry_lapse(p1, t, 1000*units.hPa)
    if t1 < xmin*units.degC:
        continue
    skew.ax.text(t1, p1, f'{t.magnitude}', fontsize=9,
                 horizontalalignment='center', color='red')

# --- wet adiabatic
t0 = np.arange(245, 320, 5)*units.K # starting points

# plot
skew.plot_moist_adiabats(t0=t0, lw=0.5, colors='green')

# put labels at 250hPa
for t in t0:
    p1 = 250 * units.hPa
    t1 = mpcalc.moist_lapse(p1, t, 1000*units.hPa)
    if t1 < xmin*units.degC:
        continue
    skew.ax.text(t1, p1, f'{t.magnitude}', fontsize=9,
                 horizontalalignment='center', color='green')

# --- saturation mixing ratio
mixing_ratio = np.array([0.2, 0.4, 0.6, 1, 2, 4, 5, 10, 15, 20, 25, 30, 35]).reshape(-1, 1) * units('g/kg')
pressure = np.arange(1000, 10, -50)*units.hPa

# plot
skew.plot_mixing_lines(mixing_ratio=mixing_ratio, pressure=pressure, lw=0.5, colors='blue')

# put labels at 110hPa
for i, mr in enumerate(mixing_ratio.flatten()):
    p1 = 110 * units.hPa + i%2 * 10 * units.hPa
    dewpt = mpcalc.dewpoint(mpcalc.vapor_pressure(p1, mr))
    if mr.magnitude < 1.0:
        skew.ax.text(dewpt, p1, f'{mr.magnitude:.1f}', fontsize=9,
                    horizontalalignment='center', color="blue")
    else:
        skew.ax.text(dewpt, p1, f'{mr.magnitude:.0f}', fontsize=9,
                    horizontalalignment='center', color="blue")
        

# fill in area corresponding CIN and CAPE
skew.shade_cin(prss_wlcl, tmpr_wlcl, prof_wlcl)
skew.shade_cape(prss_wlcl, tmpr_wlcl, prof_wlcl)

#------------------------------------------------------------------------------
# --- save 
plt.savefig(out_fig_path, transparent=False)

Executing the Program

Open a terminal window and enter:

$ cd ~/Desktop/labcode/python/plot-emagram-and-calc-params

to change the current working directory. Then, execute the program by

$ python plot-emagram-and-calc-params.py

Execution Results

When you run it, you can find an image file named emagram.png in~/Desktop/labcode/python/plot-emagram-and-calc-params, and the execution is successful if you get the image below.

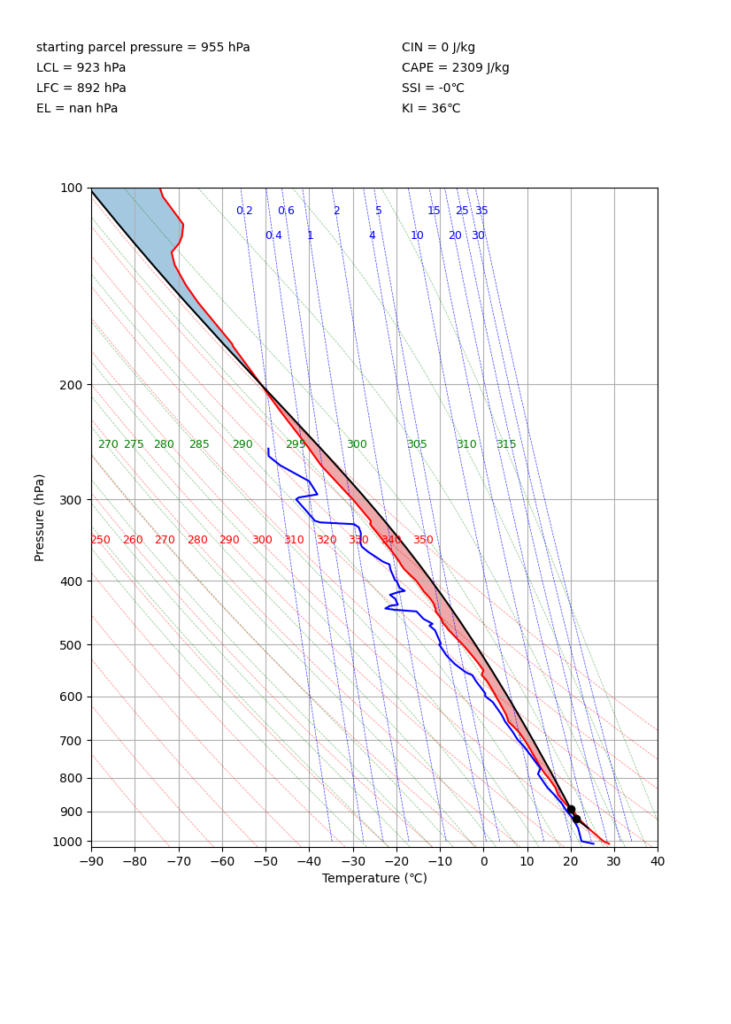
The solid red line is the temperature profile, and the solid blue line is the dew point temperature profile.

The black line plotted from around 955 hPa is the temperature profile when a 955 hPa air parcel is lifted adiabatically.

There is a black dot near 920 hPa where the black line bends. There is also a black dot near 890 hPa where the black line intersects with the solid red line. These are LCL and LFC, respectively. These values are written on the upper left side of the diagram.

Going further up, the solid black and red lines intersect again. This can be estimated as EL (approximately 200 hPa). However, the MetPy function does not seem to calculate it unless there is a dew point temperature profile (nan hPa).

On the upper right side, the values of the atmospheric stability indices explained above are written. If you just look at the values, you can see that the atmosphere is unstable. July 5, 2017, which I used as an example, is when there was heavy rain in northern Kyushu.

Explanation of the Code

We will explain the source code written above.

import matplotlib.pyplot as plt
import metpy.calc as mpcalc
from metpy.plots import SkewT
from metpy.units import units
import numpy as np

#------------------------------------------------------------------------------
# read data
fname = "20170705_09JST_47807.txt"
data = np.genfromtxt(fname=fname, unpack=True)

prss_pcl = 950 * units.hPa # pressure surface where parcel located

prss = data[0]*units.hPa # pressure
tmpr = data[1]*units.degC # temperature
rhmd = data[2] # relative humidity

First, import the necessary modules.

prss_pclis the value of the pressure surface where the starting air parcel is located. Here, it is set to 950 hPa. If you want to use one on the ground, specify a large value (for example, 10000 hPa). (However, as you will see later, in this implementation, it will be the closestprss_pcl to the pressure surface specified, so it may not be exactly the pressure surface specified.)

#------------------------------------------------------------------------------
# --- calculation
# dew point
dewp = mpcalc.dewpoint_from_relative_humidity(tmpr, rhmd/100.0)

# get index of the pressure where parcel located
i_prss_pcl = np.argmin(np.abs(prss_pcl.magnitude - prss.magnitude))

# calculate temperature evolution
prss_wlcl, tmpr_wlcl, dewp_wlcl, prof_wlcl = mpcalc.parcel_profile_with_lcl(prss[i_prss_pcl:], tmpr[i_prss_pcl:], dewp[i_prss_pcl:])

# LCL (Lifted Condensation Level)
lcl_prss, lcl_tmpr = mpcalc.lcl(prss[i_prss_pcl], tmpr[i_prss_pcl], dewp[i_prss_pcl])

# LFC (Level of Free Convection) 
lfc_prss, lfc_tmpr = mpcalc.lfc(prss[i_prss_pcl:], tmpr[i_prss_pcl:], dewp[i_prss_pcl:])

# EL (Equilibrium Level)
el_prss, el_tmpr = mpcalc.el(prss, tmpr, dewp)

# CAPE (convective available potential energy) and 
# CIN (convective inhibition)
cape, cin = mpcalc.surface_based_cape_cin(prss, tmpr, dewp)

# SSI (Shawalter Stability Index)
ssi = mpcalc.showalter_index(prss, tmpr, dewp)

# KI (K-index)
ki = mpcalc.k_index(prss, tmpr, dewp)

Perform calculations using the loaded data.

First, calculate the dew point temperature from the air temperature and relative humidity.

Next, search for the index in the loaded pressure data (=prss) that is close to the pressure specified (=prss_pcl). Let the index be i_prss_pcl.

Calculate the temperature evolution when lifting an air parcel. This is done by metpy.calc.parcel_profile_with_lcl(pressure, temperature, dewpoint).

Then, LCL, LFC, EL, CIN, CAPE, SSI, and KI are calculated one after another.

#------------------------------------------------------------------------------
# *** plot
# --- plot area
xmax = 40 # 
xmin = -90 # 
ymin = 100 # 
ymax = 1020 # 

# --- overall setting
fig = plt.figure(figsize=(210/25.4, 294/25.4), dpi=100)
out_fig_path = 'emagram.png'

# --- write comments
fig.text(0.05, 0.95, f"starting parcel pressure = {prss[i_prss_pcl].magnitude:.0f} hPa")
fig.text(0.05, 0.93, f"LCL = {lcl_prss.magnitude:.0f} hPa")
fig.text(0.05, 0.91, f"LFC = {lfc_prss.magnitude:.0f} hPa")
fig.text(0.05, 0.89, f"EL = {el_prss.magnitude:.0f} hPa")

fig.text(0.55, 0.95, f"CIN = {cin.magnitude:.0f} J/kg")
fig.text(0.55, 0.93, f"CAPE = {cape.magnitude:.0f} J/kg")
fig.text(0.55, 0.91, f"SSI = {ssi[0].magnitude:.0f}℃")
fig.text(0.55, 0.89, f"KI = {int(ki.magnitude):.0f}℃")

# --- skew T diagram 
skew = SkewT(fig, rotation=0, aspect=150)

# --- axis
skew.ax.set_xlim(xmin, xmax)
skew.ax.set_ylim(ymax, ymin)

# --- label
skew.ax.set_xlabel('Temperature (℃)')
skew.ax.set_ylabel('Pressure (hPa)')

# --- temperature, dewpoint, and wind profiles
skew.plot(prss, tmpr, 'red')
skew.plot(prss, dewp, 'blue')
skew.plot(prss_wlcl, prof_wlcl, 'black')

# --- LCL, LFC and EL
skew.plot(lcl_prss, lcl_tmpr, 'ko', markerfacecolor='black')
skew.plot(lfc_prss, lfc_tmpr, 'ko', markerfacecolor='black')

# --- dry adiabatic 
t0 = np.arange(200, 360, 10)*units.K # starting points

# plot
skew.plot_dry_adiabats(t0=t0, lw=0.5, colors='red')

# put labels at 350hPa
for t in t0:
    p1 = 350*units.hPa
    t1 = mpcalc.dry_lapse(p1, t, 1000*units.hPa)
    if t1 < xmin*units.degC:
        continue
    skew.ax.text(t1, p1, f'{t.magnitude}', fontsize=9,
                 horizontalalignment='center', color='red')

# --- wet adiabatic
t0 = np.arange(245, 320, 5)*units.K # starting points

# plot
skew.plot_moist_adiabats(t0=t0, lw=0.5, colors='green')

# put labels at 250hPa
for t in t0:
    p1 = 250 * units.hPa
    t1 = mpcalc.moist_lapse(p1, t, 1000*units.hPa)
    if t1 < xmin*units.degC:
        continue
    skew.ax.text(t1, p1, f'{t.magnitude}', fontsize=9,
                 horizontalalignment='center', color='green')

# --- saturation mixing ratio
mixing_ratio = np.array([0.2, 0.4, 0.6, 1, 2, 4, 5, 10, 15, 20, 25, 30, 35]).reshape(-1, 1) * units('g/kg')
pressure = np.arange(1000, 10, -50)*units.hPa

# plot
skew.plot_mixing_lines(mixing_ratio=mixing_ratio, pressure=pressure, lw=0.5, colors='blue')

# put labels at 110hPa
for i, mr in enumerate(mixing_ratio.flatten()):
    p1 = 110 * units.hPa + i%2 * 10 * units.hPa
    dewpt = mpcalc.dewpoint(mpcalc.vapor_pressure(p1, mr))
    if mr.magnitude < 1.0:
        skew.ax.text(dewpt, p1, f'{mr.magnitude:.1f}', fontsize=9,
                    horizontalalignment='center', color="blue")
    else:
        skew.ax.text(dewpt, p1, f'{mr.magnitude:.0f}', fontsize=9,
                    horizontalalignment='center', color="blue")
        

# fill in area corresponding CIN and CAPE
skew.shade_cin(prss_wlcl, tmpr_wlcl, prof_wlcl)
skew.shade_cape(prss_wlcl, tmpr_wlcl, prof_wlcl)

#------------------------------------------------------------------------------
# --- save 
plt.savefig(out_fig_path, transparent=False)

This part is to make an emagram. Largely this is based on the previous article,

Conclusion

In this article, we explained atmospheric stability indices that can be calculated from vertical profiles. It would be interesting to compare the profiles during heavy rain or strong wind gusts, such as tornadoes, with those during stable atmospheric conditions.