前回は時間-周波数解析手法の一つであるSTFTを紹介しました。
今回は,2つの信号の周波数空間での相関を解析する手法(コヒーレンスとフェイズ)を紹介します。
コヒーレンスとフェイズを用いると,2つの信号に含まれる周波数成分相関の強さおよび周波数成分の位相のズレを定量的に評価することができます。
macOS Big Sur, python3.7.9

コヒーレンスとフェイズ
コヒーレンスとフェイズ
2つの時系列信号データ $x(t)$ と $y(t)$ があるとします。これらをフーリエ変換したものをそれぞれ,$X(f)$ と $Y(f)$ とします。このとき,クロススペクトル (cross-spectrum) を
$$
S_{XY}(f) := X(f)Y^*(f)
$$
で定義します。$Y^*(f)$ は $Y(f)$ の複素共役を表します。
クロススペクトルは2つの信号をフーリエ変換したものの積として定義されるので,2つの信号の周波数空間での相関の大きさを表すと考えられます。
しかし,ある周波数に対して片方(たとえば,$X(f)$ のみ)が大きいだけでも,クロススペクトル $S_{XY}(f)$ は大きくなってしまいます。したがって,正規化して,このようなことが起こらないようにしたものが,(二乗) コヒーレンス (coherence)です。次のように定義されます:
$$
\mathrm{coh}_{XY}(f) := \frac{|\langle S_{XY}(f)\rangle|^2}{\langle |X(f)|^2\rangle\langle| Y(f)|^2\rangle}
$$
ここに,$\langle\cdot\rangle$ はある平均操作を表します。これを行わないと,定義により,すべての周波数 $f$ で$\mathrm{coh}^2_{XY}(f) = 1$ となってしまいます。平均化操作として,STFTでは時間または周波数方向の平均化がよく用いられます。
こうして得られたコヒーレンスは,0から1までの値を取り,2つの信号の周波数空間での(振幅の影響を除いた)相関を表します。つまり,コヒーレンスが1に近いとき,2つの信号にはその周波数成分が含まれていることになります。
ある周波数でコヒーレンスが1に近いとき,つまり,2つの信号にその周波数の成分が含まれているとき,2つの信号に含まれるその周波数成分の間の位相差を知りたいことがあります。それを教えてくれるものがフェイズ (phase)と呼ばれる量で,
$$
\theta_{XY}(f) = \arctan\left(\frac{\mathrm{Im}(\langle S_{XY}(f)\rangle)}{\mathrm{Re}(\langle S_{XY}(f)\rangle)}\right)
$$
と定義されます。
クロススペクトルが上の式で与えられるとき,
$$
\theta_{XY}(f) = \text{($x(t)$に含まれる周波数$f$成分の位相)}-\text{($y(t)$に含まれる周波数$f$成分の位相)}
$$
となります(複素共役のとり方を逆にすると符号が反転します)。
時間方向に繰り返す
以上のクロススペクトル,コヒーレンス,フェイズはDFTからSTFTに拡張したときと同様に,時間軸方向に繰り返せばクロススペクトル,コヒーレンス,フェイズの時間変化を追うことができます。
コヒーレンスとフェイズの解析コード
コヒーレンスをフェイズの解析プログラムは,次のように実装することができます。
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.patheffects as path_effects
import numpy as np
#------------------------------------------------------------------------------
# 関数を定義
# STFTを実行する関数
def STFT(t_wndw, n_stft, tm, sig):
dt = tm[1] - tm[0]
# 入力された n_wndw を t_wndwで設定した幅より小さい,かつ,2の累乗個に設定する
n_wndw = int(2**(np.floor(np.log2(t_wndw/dt))))
t_wndw = n_wndw*dt # recalculate t_wndw
n_freq = n_wndw
# 周波数
freq_sp = np.fft.fftfreq(n_wndw, dt)
# スペクトルを計算する時刻を決める
m = len(tm) - n_wndw
indxs = np.zeros(n_stft, dtype=int)
for i in range(n_stft):
indxs[i] = int(m/(n_stft+1)*(i+1)) + n_wndw//2
tm_sp = tm[indxs] # DFTをかける時刻の配列
# スペクトログラムを計算する
# スペクトルは indxs[i] - n_wndw //2 + 1 ~ indxs[i] + n_wndw//2 の n_wndw 幅で行う
sp = np.zeros((n_freq, n_stft), dtype=complex) # スペクトログラムの2次元ndarray
wndw = np.hamming(n_wndw) # hamming窓
# wndw = np.hanning(n_wndw) # hanning窓
# wndw = np.ones(n_wndw) # 矩形窓
for i in range(n_stft):
indx = indxs[i] - n_wndw//2 + 1
sp[:, i] = np.fft.fft(wndw*sig[indx:indx+n_wndw], n_wndw)/np.sqrt(n_wndw)
return freq_sp[freq_sp >= 0], tm_sp, sp[freq_sp >= 0, :]
# 時間または周波数方向に三角窓で平滑化する関数
def smoothing(sp):
n_f, n_t = sp.shape
sp_smthd = np.zeros_like(sp)
for i in range(n_t):
# krnl = np.array([1.0, 2.0, 3.0, 2.0, 1.0])
krnl = np.array([1.0, 2.0, 1.0])
sp_smthd[:, i] = np.convolve(sp[:, i], krnl, mode='same')/np.sum(krnl)
for j in range(n_t):
# krnl = np.array([1.0, 2.0, 3.0, 2.0, 1.0])
krnl = np.array([1.0, 2.0, 1.0])
sp_smthd[j, :] = np.convolve(sp_smthd[j, :], krnl, mode='same')/np.sum(krnl)
return sp_smthd
#------------------------------------------------------------------------------
# テスト信号の生成
dt = 1.0e-4
tms = 0.0
tme = 2.0
tm01 = np.arange(tms, tme, dt)
tm02 = tm01
# np.random.seed(1234)
sig01 = np.random.randn(len(tm02))*0.05
sig01[tm01 < 0.3] += np.sin(2.0*np.pi*5.0e1*tm01[tm01 < 0.3])
sig01[(0.5 < tm01) & (tm01 < 0.8)] += np.sin(2.0*np.pi*1.0e2*tm01[(0.5 < tm01) & (tm01 < 0.8)])
sig01[(1.0 < tm01) & (tm01 < 1.3)] += np.sin(2.0*np.pi*1.5e2*tm01[(1.0 < tm01) & (tm01 < 1.3)])
sig01[(1.5 < tm01) & (tm01 < 1.8)] += np.sin(2.0*np.pi*2.0e2*tm01[(1.5 < tm01) & (tm01 < 1.8)])
sig02 = np.sin(2.0*np.pi*5.0e1*tm02) + 0.1*np.sin(2.0*np.pi*1.5e2*tm02 + np.pi/2.0) + np.random.randn(len(tm02))*0.05
#------------------------------------------------------------------------------
# ウィンドウ幅,STFTを施す数の設定
t_wndw = 100.0e-3 # 100 milisecond
n_stft = 100 # number of STFT
freq_upper = 3.0e2 # 表示する周波数の上限
out_fig_path = "coh-phase.png"
#------------------------------------------------------------------------------
# STFTを実行
freq_sp01, tm_sp01, sp01 = STFT(t_wndw, n_stft, tm01, sig01)
freq_sp02, tm_sp02, sp02 = STFT(t_wndw, n_stft, tm02, sig02)
# クロススペクトル
xsp = sp01*np.conjugate(sp02)
# コヒーレンスとフェイズ
sp01_pw_smthd = smoothing(np.abs(sp01)**2) # 平滑化
sp02_pw_smthd = smoothing(np.abs(sp02)**2) # 平滑化
xsp_smthd = smoothing(xsp) # 平滑化
coh = np.abs(xsp_smthd)**2 / (sp01_pw_smthd*sp02_pw_smthd) # (二乗)コヒーレンス
phs = np.rad2deg(np.arctan2(np.imag(xsp_smthd), np.real(xsp_smthd))) # フェイズ
#------------------------------------------------------------------------------
# 結果のプロット
# 解析結果の可視化
figsize = (210/25.4, 294/25.4)
dpi = 200
fig = plt.figure(figsize=figsize, dpi=dpi)
# 図の設定 (全体)
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['xtick.top'] = True
plt.rcParams['xtick.major.size'] = 6
plt.rcParams['xtick.minor.size'] = 3
plt.rcParams['xtick.minor.visible'] = True
plt.rcParams['ytick.direction'] = 'in'
plt.rcParams['ytick.right'] = True
plt.rcParams['ytick.major.size'] = 6
plt.rcParams['ytick.minor.size'] = 3
plt.rcParams['ytick.minor.visible'] = True
plt.rcParams["font.size"] = 14
plt.rcParams['font.family'] = 'Helvetica'
# 窓関数幅をプロット上部に記載
fig.text(0.10, 0.95, f't_wndw = {t_wndw} s')
# プロット枠の設定
ax01 = fig.add_axes([0.125, 0.79, 0.70, 0.08])
ax02 = fig.add_axes([0.125, 0.59, 0.70, 0.08])
ax_sp01 = fig.add_axes([0.125, 0.68, 0.70, 0.10])
cb_sp01 = fig.add_axes([0.85, 0.68, 0.02, 0.10])
ax_sp02 = fig.add_axes([0.125, 0.48, 0.70, 0.10])
cb_sp02 = fig.add_axes([0.85, 0.48, 0.02, 0.10])
ax_xsp = fig.add_axes([0.125, 0.33, 0.70, 0.10])
cb_xsp = fig.add_axes([0.85, 0.33, 0.02, 0.10])
ax_coh = fig.add_axes([0.125, 0.22, 0.70, 0.10])
cb_coh = fig.add_axes([0.85, 0.22, 0.02, 0.10])
ax_phs = fig.add_axes([0.125, 0.10, 0.70, 0.10])
cb_phs = fig.add_axes([0.85, 0.10, 0.02, 0.10])
# ---------------------------
# テスト信号 sig01 のプロット
ax01.set_xlim(tms, tme)
ax01.set_xlabel('')
ax01.tick_params(labelbottom=False)
ax01.set_ylabel('x (sig01)')
ax01.plot(tm01, sig01, c='black')
# ---------------------------
# テスト信号 sig02 のプロット
ax02.set_xlim(tms, tme)
ax02.set_xlabel('')
ax02.tick_params(labelbottom=False)
ax02.set_ylabel('y (sig02)')
ax02.plot(tm02, sig02, c='black')
# ---------------------------
# テスト信号 sig01 のスペクトログラムのプロット
ax_sp01.set_xlim(tms, tme)
ax_sp01.set_xlabel('')
ax_sp01.tick_params(labelbottom=False)
ax_sp01.set_ylim(0, freq_upper)
ax_sp01.set_ylabel('frequency\n(Hz)')
norm = mpl.colors.Normalize(vmin=np.log10(np.abs(sp01[freq_sp01 < freq_upper, :])**2).min(),
vmax=np.log10(np.abs(sp01[freq_sp01 < freq_upper, :])**2).max())
cmap = mpl.cm.jet
ax_sp01.contourf(tm_sp01, freq_sp01, np.log10(np.abs(sp01)**2),
norm=norm, levels=256, cmap=cmap)
ax_sp01.text(0.99, 0.97, "spectrogram", color='white', ha='right', va='top',
path_effects=[path_effects.Stroke(linewidth=2, foreground='black'),
path_effects.Normal()],
transform=ax_sp01.transAxes)
mpl.colorbar.ColorbarBase(cb_sp01, cmap=cmap, norm=norm,
orientation="vertical",
label='$\log_{10}|X/N|^2$')
# ---------------------------
# テスト信号 sig02 のスペクトログラムのプロット
ax_sp02.set_xlim(tms, tme)
ax_sp02.set_xlabel('')
ax_sp02.tick_params(labelbottom=True)
ax_sp02.set_ylim(0, freq_upper)
ax_sp02.set_ylabel('frequency\n(Hz)')
norm = mpl.colors.Normalize(vmin=np.log10(np.abs(sp02[freq_sp02 < freq_upper, :])**2).min(),
vmax=np.log10(np.abs(sp02[freq_sp02 < freq_upper, :])**2).max())
ax_sp02.contourf(tm_sp02, freq_sp02, np.log10(np.abs(sp02)**2),
norm=norm, levels=256, cmap=cmap)
ax_sp02.text(0.99, 0.97, "spectrogram", color='white', ha='right', va='top',
path_effects=[path_effects.Stroke(linewidth=2, foreground='black'),
path_effects.Normal()],
transform=ax_sp02.transAxes)
mpl.colorbar.ColorbarBase(cb_sp02, cmap=cmap, norm=norm,
orientation="vertical",
label='$\log_{10}|Y/N|^2$')
# ---------------------------
# テスト信号 sig01 と sig02 のクロススペクトルのプロット
ax_xsp.set_xlim(tms, tme)
ax_xsp.set_xlabel('')
ax_xsp.tick_params(labelbottom=False)
ax_xsp.set_ylim(0, freq_upper)
ax_xsp.set_ylabel('frequency\n(Hz)')
norm = mpl.colors.Normalize(vmin=np.log10(np.abs(xsp[freq_sp02 < freq_upper, :])).min(),
vmax=np.log10(np.abs(xsp[freq_sp02 < freq_upper, :])).max())
ax_xsp.contourf(tm_sp01, freq_sp01, np.log10(np.abs(xsp)),
norm=norm, levels=256, cmap=cmap)
ax_xsp.text(0.99, 0.97, "cross-spectrum", color='white', ha='right', va='top',
path_effects=[path_effects.Stroke(linewidth=2, foreground='black'),
path_effects.Normal()],
transform=ax_xsp.transAxes)
mpl.colorbar.ColorbarBase(cb_xsp, cmap=cmap, norm=norm,
orientation="vertical",
label='$\log_{10}|XY^*/N^2|$')
# ---------------------------
# テスト信号 sig01 と sig02 のコヒーレンスのプロット
ax_coh.set_xlim(tms, tme)
ax_coh.set_xlabel('')
ax_coh.tick_params(labelbottom=False)
ax_coh.set_ylim(0, freq_upper)
ax_coh.set_ylabel('frequency\n(Hz)')
norm = mpl.colors.Normalize(vmin=0.0, vmax=1.0)
ax_coh.contourf(tm_sp01, freq_sp01, coh,
norm=norm, levels=10, cmap=cmap)
ax_coh.text(0.99, 0.97, "coherence", color='white', ha='right', va='top',
path_effects=[path_effects.Stroke(linewidth=2, foreground='black'),
path_effects.Normal()],
transform=ax_coh.transAxes)
mpl.colorbar.ColorbarBase(cb_coh, cmap=cmap, norm=norm,
boundaries=np.linspace(0, 1, 11),
orientation="vertical",
label='coherence')
# ---------------------------
# テスト信号 sig01 と sig02 のフェイズのプロット
ax_phs.set_xlim(tms, tme)
ax_phs.set_xlabel('time (s)')
ax_phs.tick_params(labelbottom=True)
ax_phs.set_ylim(0, freq_upper)
ax_phs.set_ylabel('frequency\n(Hz)')
norm = mpl.colors.Normalize(vmin=-180.0, vmax=180.0)
cmap = mpl.cm.hsv
ax_phs.contourf(tm_sp01, freq_sp01, np.where(coh >= 0.75, phs, None),
norm=norm, levels=16, cmap=cmap)
ax_phs.text(0.99, 0.97, "phase", color='white', ha='right', va='top',
path_effects=[path_effects.Stroke(linewidth=2, foreground='black'),
path_effects.Normal()],
transform=ax_phs.transAxes)
mpl.colorbar.ColorbarBase(cb_phs, cmap=cmap,
norm=norm,
boundaries=np.linspace(-180.0, 180.0, 17),
orientation="vertical",
label='phase (deg)')
#-----------------------------------------------------------------------------
# 図の出力
plt.savefig(out_fig_path, transparent=False)プログラムを実行する
上で記述したコードは coh-phase-demo.pyという名前のファイルとして,好きなディレクトリ(ここでは~/Desktop/LabCode/python/coh-phaseとします)に保存します。
ターミナルを開き,
$ cd Desktop/LabCode/python/coh-phaseと入力し,ディレクトリを移動します。あとは以下のコマンドでcoh-phase-demo.py を実行するだけです。( $マークは無視してください)。
$ python3 coh-phase-demo.py実行結果
~/Desktop/LabCode/python/coh-phase にcoh-phase.pngというファイルができて,以下のようになっていれば成功です!
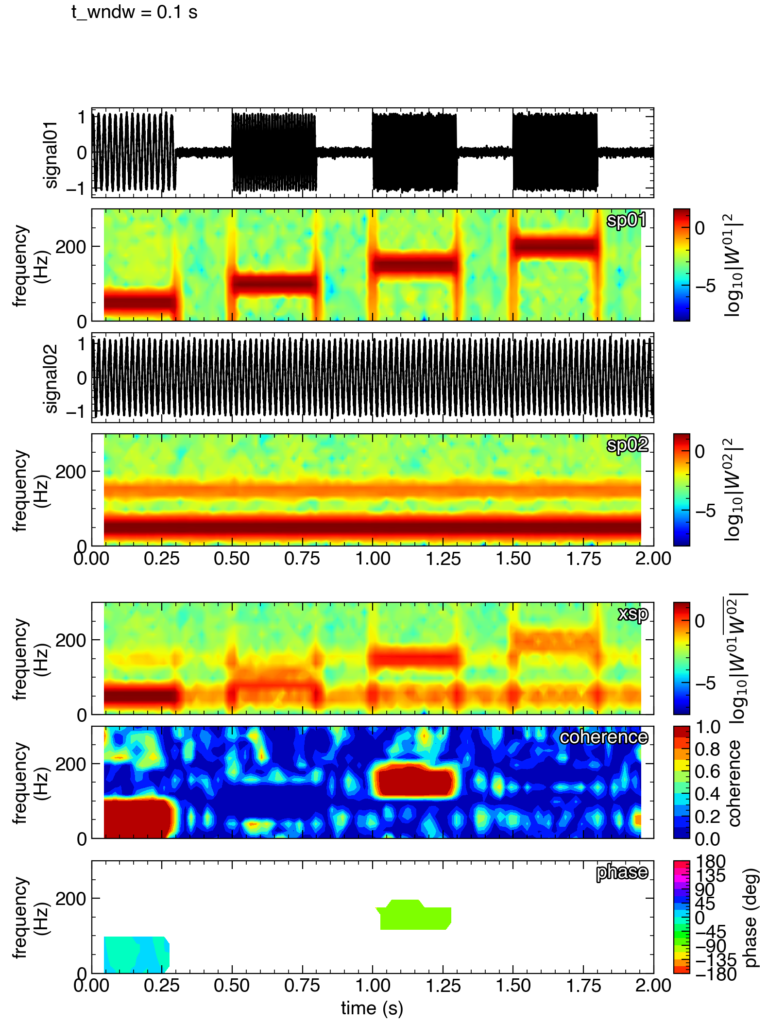
一段目から四段目はテスト信号とそのスペクトログラムです。
テスト信号として,
$$
\mathrm{sig01}(t) = \mathcal{N}_{\mu=0, \sigma=0.05}(t) + \begin{cases}\sin(2\pi\times 50\times t), & 0\ \mathrm{s}\le t < 0.3\ \mathrm{s}, \\\sin(2\pi\times 100\times t), & 0.5\ \mathrm{s} <t < 0.8\ \mathrm{s}, \\\sin(2\pi\times 150\times t), & 1.0\ \mathrm{s} < t < 1.3\ \mathrm{s}, \\\sin(2\pi\times 200\times t), &1.5 \ \mathrm{s}< t < 1.8\ \mathrm{s}, \end{cases},
$$
$$
\\\mathrm{sig02}(t) = \mathcal{N}_{\mu=0, \sigma=0.05}(t) + \sin(2\pi\times 50\times t) +0.1\sin(2\pi\times 150\times t + \pi/2)
$$
が用いられています。ここで,$\mathcal{N}_{\mu=0, \sigma=0.05}(t)$ は平均0,標準偏差0.05のガウシアンノイズを表します。sig02に含まれる150 kHzの成分はsig01よりも90度 (=π/2 ラジアン) 進んだものを入れています(たとえば,$\sin(x)$ と$\sin(x+\pi/2) = \cos(x)$ のグラフを考えてください。
五段目はクロススペクトルを示しています。
六段目はコヒーレンス,七段目はフェイズです。コヒーレンスは2つの信号に含まれる周波数成分が一致するとき,つまり,0 s ~ 0.3 sと1.0 s~ 1.3 sにおいて,それぞれ,50 Hz付近と150 kHz付近で,1に近くなっていることがわかります。
また,その時のフェイズ(位相差)はそれぞれ,0度(sig01に含まれる50 kHzの成分とsig02に含まれる50 kHzの成分の位相の間にずれはない)と–90度(sig01に含まれる150 kHzの成分は,sig02に含まれる150 kHzの成分よりも位相が90度遅れている)となっており,テスト信号から想定される結果通りとなっています。
コードの解説
コードの解説をしていきます。
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.patheffects as path_effects
import numpy as np必要なモジュールをインポートします。
#------------------------------------------------------------------------------
# 関数を定義
# STFTを実行する関数
def STFT(t_wndw, n_stft, tm, sig):
dt = tm[1] - tm[0]
# 入力された n_wndw を t_wndwで設定した幅より小さい,かつ,2の累乗個に設定する
n_wndw = int(2**(np.floor(np.log2(t_wndw/dt))))
t_wndw = n_wndw*dt # recalculate t_wndw
n_freq = n_wndw
# 周波数
freq_sp = np.fft.fftfreq(n_wndw, dt)
# スペクトルを計算する時刻を決める
m = len(tm) - n_wndw
indxs = np.zeros(n_stft, dtype=int)
for i in range(n_stft):
indxs[i] = int(m/(n_stft+1)*(i+1)) + n_wndw//2
tm_sp = tm[indxs] # DFTをかける時刻の配列
# スペクトログラムを計算する
# スペクトルは indxs[i] - n_wndw //2 + 1 ~ indxs[i] + n_wndw//2 の n_wndw 幅で行う
sp = np.zeros((n_freq, n_stft), dtype=complex) # スペクトログラムの2次元ndarray
wndw = np.hamming(n_wndw) # hamming窓
# wndw = np.hanning(n_wndw) # hanning窓
# wndw = np.ones(n_wndw) # 矩形窓
for i in range(n_stft):
indx = indxs[i] - n_wndw//2 + 1
sp[:, i] = np.fft.fft(wndw*sig[indx:indx+n_wndw], n_wndw)/np.sqrt(n_wndw)
return freq_sp[freq_sp >= 0], tm_sp, sp[freq_sp >= 0, :]
# 時間または周波数方向に三角窓で平滑化する関数
def smoothing(sp):
n_f, n_t = sp.shape
sp_smthd = np.zeros_like(sp)
for i in range(n_t):
# krnl = np.array([1.0, 2.0, 3.0, 2.0, 1.0])
krnl = np.array([1.0, 2.0, 1.0])
sp_smthd[:, i] = np.convolve(sp[:, i], krnl, mode='same')/np.sum(krnl)
for j in range(n_t):
# krnl = np.array([1.0, 2.0, 3.0, 2.0, 1.0])
krnl = np.array([1.0, 2.0, 1.0])
sp_smthd[j, :] = np.convolve(sp_smthd[j, :], krnl, mode='same')/np.sum(krnl)
return sp_smthd繰り返し用いるSTFTと平滑化を関数として定義しておきます。関数STFTは前回の記事で詳しく説明しています。なお,0以上の周波数成分しか必要ないため,負の周波数部分はカットして出力するようにしています。
関数smoothingは入力スペクトログラムspに対して周波数方向と時間方向に移動平均を使用して平滑化する関数です。三角窓で平滑化します。三角窓の幅は3を使用しています。krnlを変更することで,移動平均に使用する窓関数を変更することができます。
#------------------------------------------------------------------------------
# テスト信号の生成
dt = 1.0e-4
tms = 0.0
tme = 2.0
tm01 = np.arange(tms, tme, dt)
tm02 = tm01
# np.random.seed(1234)
sig01 = np.random.randn(len(tm02))*0.05
sig01[tm01 < 0.3] += np.sin(2.0*np.pi*5.0e1*tm01[tm01 < 0.3])
sig01[(0.5 < tm01) & (tm01 < 0.8)] += np.sin(2.0*np.pi*1.0e2*tm01[(0.5 < tm01) & (tm01 < 0.8)])
sig01[(1.0 < tm01) & (tm01 < 1.3)] += np.sin(2.0*np.pi*1.5e2*tm01[(1.0 < tm01) & (tm01 < 1.3)])
sig01[(1.5 < tm01) & (tm01 < 1.8)] += np.sin(2.0*np.pi*2.0e2*tm01[(1.5 < tm01) & (tm01 < 1.8)])
sig02 = np.sin(2.0*np.pi*5.0e1*tm02) + 0.1*np.sin(2.0*np.pi*1.5e2*tm02 + np.pi/2.0) + np.random.randn(len(tm02))*0.05テスト信号を生成します。上で述べたように,テスト信号として
$$
\mathrm{sig01}(t) = \mathcal{N}_{\mu=0, \sigma=0.05}(t) + \begin{cases}\sin(2\pi\times 50\times t), & 0\ \mathrm{s}\le t < 0.3\ \mathrm{s}, \\\sin(2\pi\times 100\times t), & 0.5\ \mathrm{s} <t < 0.8\ \mathrm{s}, \\\sin(2\pi\times 150\times t), & 1.0\ \mathrm{s} < t < 1.3\ \mathrm{s}, \\\sin(2\pi\times 200\times t), &1.5 \ \mathrm{s}< t < 1.8\ \mathrm{s}, \end{cases},
$$
$$
\\\mathrm{sig02}(t) = \mathcal{N}_{\mu=0, \sigma=0.05}(t) + \sin(2\pi\times 50\times t) +0.1\sin(2\pi\times 150\times t + \pi/2)
$$
を用いました。
#------------------------------------------------------------------------------
# ウィンドウ幅,STFTを施す数の設定
t_wndw = 100.0e-3 # 100 milisecond
n_stft = 100 # number of STFT
freq_upper = 3.0e2 # 表示する周波数の上限
out_fig_path = "coh-phase.png"ウィンドウ幅や与えられたデータに対してSTFTの回数を施す回数,表示周波数の上限と出力ファイルの名前を設定します。
#------------------------------------------------------------------------------
# STFTを実行
freq_sp01, tm_sp01, sp01 = STFT(t_wndw, n_stft, tm01, sig01)
freq_sp02, tm_sp02, sp02 = STFT(t_wndw, n_stft, tm02, sig02)
# クロススペクトル
xsp = sp01*np.conjugate(sp02)
# コヒーレンスとフェイズ
sp01_pw_smthd = smoothing(np.abs(sp01)**2) # 平滑化
sp02_pw_smthd = smoothing(np.abs(sp02)**2) # 平滑化
xsp_smthd = smoothing(xsp) # 平滑化
coh = np.abs(xsp_smthd)**2 / (sp01_pw_smthd*sp02_pw_smthd) # (二乗)コヒーレンス
phs = np.rad2deg(np.arctan2(np.imag(xsp_smthd), np.real(xsp_smthd))) # フェイズSTFTを実行し,上で説明したように,平均化の操作を実行した後,コヒーレンスとフェイズを計算します。
#------------------------------------------------------------------------------
# 結果のプロット
# 解析結果の可視化
figsize = (210/25.4, 294/25.4)
dpi = 200
fig = plt.figure(figsize=figsize, dpi=dpi)
# 図の設定 (全体)
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['xtick.top'] = True
plt.rcParams['xtick.major.size'] = 6
plt.rcParams['xtick.minor.size'] = 3
plt.rcParams['xtick.minor.visible'] = True
plt.rcParams['ytick.direction'] = 'in'
plt.rcParams['ytick.right'] = True
plt.rcParams['ytick.major.size'] = 6
plt.rcParams['ytick.minor.size'] = 3
plt.rcParams['ytick.minor.visible'] = True
plt.rcParams["font.size"] = 14
plt.rcParams['font.family'] = 'Helvetica'
# 窓関数幅をプロット上部に記載
fig.text(0.10, 0.95, f't_wndw = {t_wndw} s')
# プロット枠の設定
ax01 = fig.add_axes([0.125, 0.79, 0.70, 0.08])
ax02 = fig.add_axes([0.125, 0.59, 0.70, 0.08])
ax_sp01 = fig.add_axes([0.125, 0.68, 0.70, 0.10])
cb_sp01 = fig.add_axes([0.85, 0.68, 0.02, 0.10])
ax_sp02 = fig.add_axes([0.125, 0.48, 0.70, 0.10])
cb_sp02 = fig.add_axes([0.85, 0.48, 0.02, 0.10])
ax_xsp = fig.add_axes([0.125, 0.33, 0.70, 0.10])
cb_xsp = fig.add_axes([0.85, 0.33, 0.02, 0.10])
ax_coh = fig.add_axes([0.125, 0.22, 0.70, 0.10])
cb_coh = fig.add_axes([0.85, 0.22, 0.02, 0.10])
ax_phs = fig.add_axes([0.125, 0.10, 0.70, 0.10])
cb_phs = fig.add_axes([0.85, 0.10, 0.02, 0.10])
# ---------------------------
# テスト信号 sig01 のプロット
ax01.set_xlim(tms, tme)
ax01.set_xlabel('')
ax01.tick_params(labelbottom=False)
ax01.set_ylabel('x (sig01)')
ax01.plot(tm01, sig01, c='black')
# ---------------------------
# テスト信号 sig02 のプロット
ax02.set_xlim(tms, tme)
ax02.set_xlabel('')
ax02.tick_params(labelbottom=False)
ax02.set_ylabel('y (sig02)')
ax02.plot(tm02, sig02, c='black')
# ---------------------------
# テスト信号 sig01 のスペクトログラムのプロット
ax_sp01.set_xlim(tms, tme)
ax_sp01.set_xlabel('')
ax_sp01.tick_params(labelbottom=False)
ax_sp01.set_ylim(0, freq_upper)
ax_sp01.set_ylabel('frequency\n(Hz)')
norm = mpl.colors.Normalize(vmin=np.log10(np.abs(sp01[freq_sp01 < freq_upper, :])**2).min(),
vmax=np.log10(np.abs(sp01[freq_sp01 < freq_upper, :])**2).max())
cmap = mpl.cm.jet
ax_sp01.contourf(tm_sp01, freq_sp01, np.log10(np.abs(sp01)**2),
norm=norm, levels=256, cmap=cmap)
ax_sp01.text(0.99, 0.97, "spectrogram", color='white', ha='right', va='top',
path_effects=[path_effects.Stroke(linewidth=2, foreground='black'),
path_effects.Normal()],
transform=ax_sp01.transAxes)
mpl.colorbar.ColorbarBase(cb_sp01, cmap=cmap, norm=norm,
orientation="vertical",
label='$\log_{10}|X/N|^2$')
# ---------------------------
# テスト信号 sig02 のスペクトログラムのプロット
ax_sp02.set_xlim(tms, tme)
ax_sp02.set_xlabel('')
ax_sp02.tick_params(labelbottom=True)
ax_sp02.set_ylim(0, freq_upper)
ax_sp02.set_ylabel('frequency\n(Hz)')
norm = mpl.colors.Normalize(vmin=np.log10(np.abs(sp02[freq_sp02 < freq_upper, :])**2).min(),
vmax=np.log10(np.abs(sp02[freq_sp02 < freq_upper, :])**2).max())
ax_sp02.contourf(tm_sp02, freq_sp02, np.log10(np.abs(sp02)**2),
norm=norm, levels=256, cmap=cmap)
ax_sp02.text(0.99, 0.97, "spectrogram", color='white', ha='right', va='top',
path_effects=[path_effects.Stroke(linewidth=2, foreground='black'),
path_effects.Normal()],
transform=ax_sp02.transAxes)
mpl.colorbar.ColorbarBase(cb_sp02, cmap=cmap, norm=norm,
orientation="vertical",
label='$\log_{10}|Y/N|^2$')
# ---------------------------
# テスト信号 sig01 と sig02 のクロススペクトルのプロット
ax_xsp.set_xlim(tms, tme)
ax_xsp.set_xlabel('')
ax_xsp.tick_params(labelbottom=False)
ax_xsp.set_ylim(0, freq_upper)
ax_xsp.set_ylabel('frequency\n(Hz)')
norm = mpl.colors.Normalize(vmin=np.log10(np.abs(xsp[freq_sp02 < freq_upper, :])).min(),
vmax=np.log10(np.abs(xsp[freq_sp02 < freq_upper, :])).max())
ax_xsp.contourf(tm_sp01, freq_sp01, np.log10(np.abs(xsp)),
norm=norm, levels=256, cmap=cmap)
ax_xsp.text(0.99, 0.97, "cross-spectrum", color='white', ha='right', va='top',
path_effects=[path_effects.Stroke(linewidth=2, foreground='black'),
path_effects.Normal()],
transform=ax_xsp.transAxes)
mpl.colorbar.ColorbarBase(cb_xsp, cmap=cmap, norm=norm,
orientation="vertical",
label='$\log_{10}|XY^*/N^2|$')
# ---------------------------
# テスト信号 sig01 と sig02 のコヒーレンスのプロット
ax_coh.set_xlim(tms, tme)
ax_coh.set_xlabel('')
ax_coh.tick_params(labelbottom=False)
ax_coh.set_ylim(0, freq_upper)
ax_coh.set_ylabel('frequency\n(Hz)')
norm = mpl.colors.Normalize(vmin=0.0, vmax=1.0)
ax_coh.contourf(tm_sp01, freq_sp01, coh,
norm=norm, levels=10, cmap=cmap)
ax_coh.text(0.99, 0.97, "coherence", color='white', ha='right', va='top',
path_effects=[path_effects.Stroke(linewidth=2, foreground='black'),
path_effects.Normal()],
transform=ax_coh.transAxes)
mpl.colorbar.ColorbarBase(cb_coh, cmap=cmap, norm=norm,
boundaries=np.linspace(0, 1, 11),
orientation="vertical",
label='coherence')
# ---------------------------
# テスト信号 sig01 と sig02 のフェイズのプロット
ax_phs.set_xlim(tms, tme)
ax_phs.set_xlabel('time (s)')
ax_phs.tick_params(labelbottom=True)
ax_phs.set_ylim(0, freq_upper)
ax_phs.set_ylabel('frequency\n(Hz)')
norm = mpl.colors.Normalize(vmin=-180.0, vmax=180.0)
cmap = mpl.cm.hsv
ax_phs.contourf(tm_sp01, freq_sp01, np.where(coh >= 0.75, phs, None),
norm=norm, levels=16, cmap=cmap)
ax_phs.text(0.99, 0.97, "phase", color='white', ha='right', va='top',
path_effects=[path_effects.Stroke(linewidth=2, foreground='black'),
path_effects.Normal()],
transform=ax_phs.transAxes)
mpl.colorbar.ColorbarBase(cb_phs, cmap=cmap,
norm=norm,
boundaries=np.linspace(-180.0, 180.0, 17),
orientation="vertical",
label='phase (deg)')
#-----------------------------------------------------------------------------
# 図の出力
plt.savefig(out_fig_path, transparent=False)解析の結果をプロットします。前半の4つのプロット部分は前回の記事で詳しく説明したものと同じです。
後半3つ(クロススペクトル,コヒーレンス,フェイズ)に関してもほとんど同じですが,contourfのlevelsオプションでlevels=10やlevels=17として,わざと離散的に表現しています。
また,フェイズのカラーマップはhsvとし,–180度と180度が滑らかにつながるようにしています。フェイズはコヒーレンスが1に近い周波数でのみ意味を持ちますので,コヒーレンスが0.75以上の場合にのみ表示するようにしています。
最後に
今回は2つの信号の間の周波数空間での相関を解析するコヒーレンスとフェイズについて紹介しました。この手法を使うと,2つの信号に共通に含まれる周波数成分を見つけることができ,また,それらの周波数成分の位相のズレを定量的に評価することができます。




