【PySCF】構造最適化・振動数計算のやり方【Pythonで始める量子化学計算】

この記事では、Pythonで利用可能な量子化学計算ライブラリ「Pyscf」を用いた構造最適化と振動数計算について詳しく解説しています。無料で利用できるPyscfを使用して、ここではDFT計算による構造最適化を中心に、分子の最適化から可視化、そして虚振動の確認に至るまでのプロセスを一貫して説明しています。Pyscfを用いて安定した分子構造を得る方法をマスターすることができ、機械学習による科学研究や開発に役立てることが可能になります。

Gaussianを使った量子化学計算の初心者向け技術書を販売中

¥2,000 → ¥1,000 今なら50%OFF!!

しばしば出くわすエラーへの対処法をはじめ
Gaussianと無料ソフトウェア Avogadro を組み合わせた物性解析手法が学べます！

技術書ページへ

今回使用するPyscf, Avogadro, py3Dmolは以下の目的で利用しています。

• Pyscf : 構造最適化計算・振動数計算の実行
• Avogadro : 分子構造座標作成
• py3Dmol：Google colab上で分子の可視化

量子化学計算用のソフトウェア: PySCFとは

PySCF（Python Simulations of Chemistry Framework）は、Pythonで書かれた無料・商用利用が可能なオープンソースの量子化学計算Pythonライブラリです。PySCFは特に電子構造計算に対応しており、密度汎関数理論（DFT）、ハートリー・フォック法、ポストハートリー・フォック法など多様な計算手法をサポートしています。利用者はPythonを用いて容易に計算セットアップを行うことができ、拡張性とカスタマイズの自由度が高いため、研究開発に適しています。[1]。

参考文献[1]から引用

構造最適化計算とは？

構造最適化計算は、与えられた分子の原子の配置を変化させ、分子の全エネルギーが最小になる立体構造を見つけるための計算手法です。このプロセスでは、分子の構造がエネルギー的に最も安定した形へと収束するように原子間距離や角度を調整します。

PySCFを使用した構造最適化では、分子の初期構造から出発して、以下のステップに従って計算が進行します：

1. エネルギーの計算： 分子の初期構造に基づいて、全エネルギーを計算します。このエネルギーは、電子構造計算により得られます。
2. 勾配の計算： 分子の各原子に対するエネルギーの勾配（エネルギーの微分値）を計算します。勾配は、分子のどの原子がどの方向に動けばエネルギーが低下するかを示します。
3. 原子の移動： 計算された勾配に基づいて原子を動かし、エネルギーがさらに低くなる新しい配置を求めます。
4. 収束の判断： 新しい構造のエネルギーと勾配を再計算し、これを収束基準（例えば、エネルギーの変化が一定値以下になるなど）が満たされるまで繰り返します。
5. 最終構造の決定： 収束基準を満たすと、計算は終了し、得られた構造がその分子の安定な構造として採用されます。

構造最適化を行うことで、実験的に観測される分子構造の予測や、未知の分子の安定構造の探索などが可能になります。PySCFを利用することで、これらの計算を効率的かつ正確に行うことができ、分子設計や材料科学の分野での応用が期待されます。

分子構造作成

分子モデリングの基本

分子モデリングは、水分子のような単純な分子から複雑で大きな分子まで、分子の初期構造を設計する上で不可欠です。この初期構造が後の計算の基盤となります。Avogadroをはじめとする多くの分子モデリングツールが利用可能で、以下にいくつかの主要なツールを紹介します：

• Avogadro: 分子の3D構造を直感的に作成・編集できるフリーソフトウェアです。[2]
• GaussView、Facio、GabEdit、MacMolPlt、Molby、MASK、Winmostar: これらも広く使用されるフリー及び有償のソフトウェアで、分子設計と可視化に役立ちます。
• MolView: ウェブベースのツールで、アクセスが容易です。

ケモインフォマティクスを利用した構造生成

RDKitなどのケモインフォマティクスライブラリを用いて、SMILESやSDFファイルから3次元構造を自動生成する方法もあります。この技術は、大量の分子データを効率的に扱う際に特に有効です。

実践例：1,2-ジフルオロエタンのモデリング

具体的な例として、1,2-ジフルオロエタンの分子モデリングをAvogadroで行います。細かな分子設計の詳細はこちらの記事で取り上げており、そちらにはAogadroのインストール方法も記載されています。初めて構造最適化を試す方は、提供されたサンプル座標を使用してみてください。

Avogadroから座標を抽出

今回はAvogadroで1,2-ジフルオロエタンを作成し、力場による簡易的な構造最適化が終了していることを想定して始めます。

1. AvogadroのメニューバーからBuildを選択し、Cartesian Editer を選択してください。

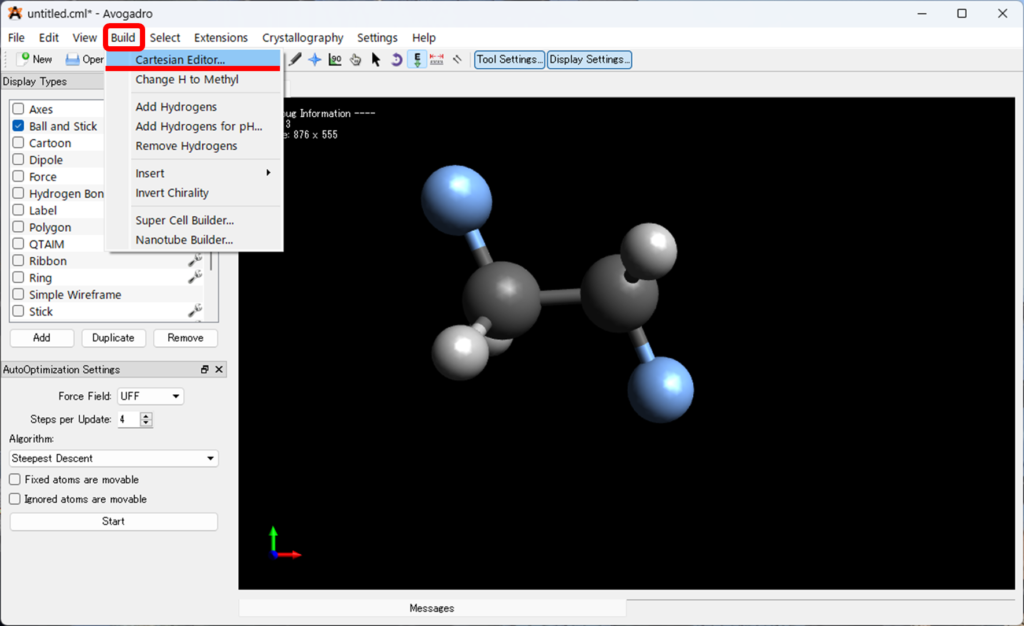
2. 画像と同じように上・左下のプルダウンがElement、Angstroms、XYZになっている事を確認してください。

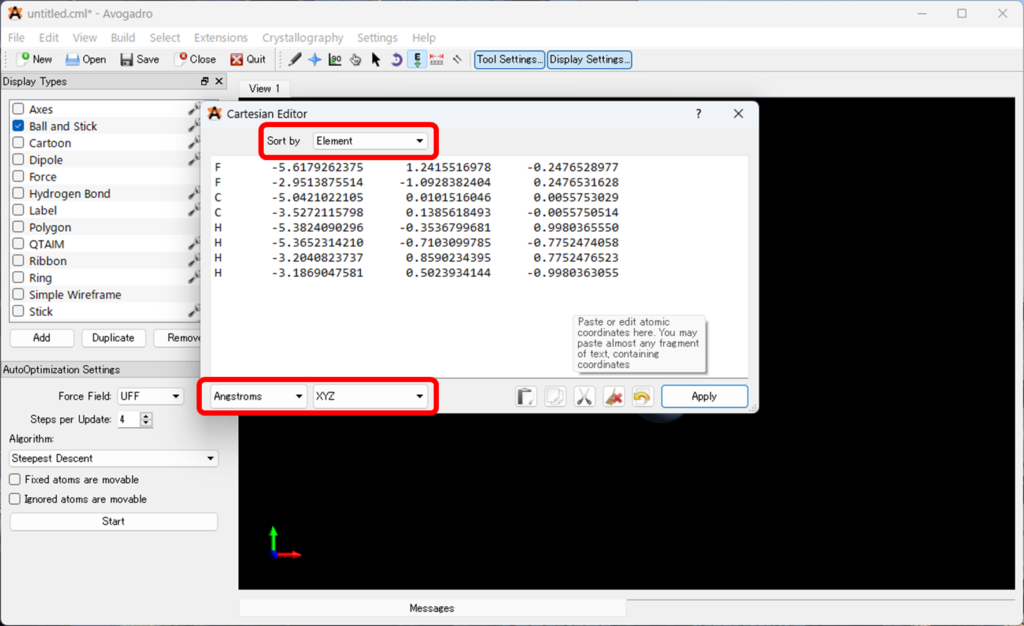
3. 座標を全てコピーしてください。以下のような座標が得られると思います。

F       -5.6179262375      1.2415516978     -0.2476528977                 
F       -2.9513875514     -1.0928382404      0.2476531628                 
C       -5.0421022105      0.0101516046      0.0055753029                 
C       -3.5272115798      0.1385618493     -0.0055750514                 
H       -5.3824090296     -0.3536799681      0.9980365550                 
H       -5.3652314210     -0.7103099785     -0.7752474058                 
H       -3.2040823737      0.8590234395      0.7752476523                 
H       -3.1869047581      0.5023934144     -0.9980363055                 

PySCFを使った構造最適化の準備

概要

では構造最適化の準備を行っていきます。今回はGoogle Colabを使って実行します。

Google Colabは、ブラウザベースのPythonプログラミング環境であり、PySCFを使用するのに適したプラットフォームの一つです。Google Colabを使用することで、ローカル環境のセットアップなしにPySCFの計算をすぐに開始することができます。

Google colabのリンク：https://colab.research.google.com/?hl=ja

PySCFは、密度汎関数理論（DFT）とハートリー・フォック（HF）理論を用いた構造最適化をサポートしています。DFTの構造最適化にはgeometric、HFにはpybernyという外部ツールが必要です。この記事では、DFTを用いた構造最適化の準備として、geometricのインストール手順を説明します。

インストール手順

ColabノートブックでPySCFを使用するには、まず以下のコマンドをセルに入力して実行し、PySCF、および構造最適化行う為に必要なライブラリをインストールします。ローカル環境でインストールする際は！を取って実行してください。

!pip install pyscf
!pip install numpy
!pip install geometric

文献の記載

構造最適化の結果を研究に使用する際は、PySCF[3-6]と使用したツール（本例ではgeometric）の文献[6]を参照する必要があることに注意してください。

構造最適化の設定

今回は、密度汎関数理論（DFT）を用いて構造最適化を行います。計算にはB3LYP汎関数と6-31+G(d)基底関数を使用し、分子の安定構造を探索します。他の汎関数（例えば、TPSS, M06-2X, CAM-B3LYP）やDunning系のaug-cc-pVXZなどの基底関数も選択可能です。

パスの設定とフォルダの作成

まずは計算結果を保存するためのフォルダとファイル名を設定するために、Google ColabでGoogle Driveをマウントし、必要に応じて新しいフォルダを作成する手順を含めます。これにより、計算結果を整理しやすく、アクセスも簡単になります。

Google Driveのマウント

Google Colabを使用する際は、まずGoogle Driveをマウントして、データの保存と読み込みが行えるようにします。

from google.colab import drive
drive.mount('/content/drive')

フォルダの作成とパスの設定

計算結果を保存するフォルダがまだ存在しない場合は、Pythonを使用して新しくフォルダを作成することができます。以下のコードでは、指定したパスにフォルダが存在しない場合に限り、新しいフォルダを作成します。

import os

# 計算結果を保存するパスを設定
folder_path = "/content/drive/MyDrive/pyscf"
base_filename = "cfcf"

# フルパスの設定
path = os.path.join(folder_path, base_filename)

# フォルダが存在しない場合は作成
if not os.path.exists(folder_path):
    os.makedirs(folder_path)
    print(f"Created folder: {folder_path}")

# 例としてチェックポイントファイル名の設定
checkpoint_file = path + ".chk"
print(f"Checkpoint file will be saved as: {checkpoint_file}")



この設定により、/content/drive/MyDrive/pyscf ディレクトリ下に cfcf.chk というチェックポイントファイルを保存することができます。この方法を用いることで、計算が終了した後もファイルが整然と保存され、必要な時にすぐに見つけることができます。

この手順を適切に行うことで、万が一の計算途中の停止にも迅速に対応できるようになります。

分子の定義

分子の定義は、PySCFのgto.Mメソッドを使用して行います。このメソッドでは、原子の座標、基底関数、分子の電荷、スピン多重度、対称性の有無などの重要な情報を指定します。

from pyscf import gto

mol = gto.M(
    atom='''
    F       -2.9513875514     -1.0928382404      0.2476531628
    F       -5.6179262375      1.2415516978     -0.2476528977
    C       -3.5272115798      0.1385618493     -0.0055750514
    C       -5.0421022105      0.0101516046      0.0055753029
    H       -3.1869047581      0.5023934144     -0.9980363055
    H       -3.2040823737      0.8590234395      0.7752476523
    H       -5.3652314210     -0.7103099785     -0.7752474058
    H       -5.3824090296     -0.3536799681      0.9980365550
    ''',
    basis='6-31G(d)',
    charge=0,  # 分子の全体の電荷
    spin=0,    # スピン多重度 (2S), S=0 でシングレット状態
    symmetry=True,  # 分子の対称性を利用するかどうか
    verbose=4  # 詳細な計算ログの出力レベル
)



詳細説明:

• atom: 分子を構成する各原子の種類と3次元空間での座標をリストします。
• basis: 使用する基底関数セットを指定します。ここでは、6-31G(d)基底を使用しています。
• charge: 分子の全体の電荷を指定します。中性分子では0となります。
• spin: 分子のスピン多重度を指定します。注意点として、PySCFではスピンの指定にspin属性を使用しますが、これは分子の未対電子の総数（2S）であり、伝統的な量子化学の2S+1とは異なります。したがって、ダブレット状態の分子（1つの未対電子）ではspin=1、トリプレット状態（2つの未対電子）ではspin=2を使用します。
• symmetry: 分子の対称性を考慮して計算を行うかどうかを指定します。対称性を考慮すると計算効率が向上することがあります。Gaussianのnonsymオプションと同じです。
• verbose: 計算中に出力される情報の量を制御します。verbose=4は非常に詳細な情報を出力します。

この設定を使用することで、計算前に分子の3D構造が正確に設定され、計算中の進行状況を詳しく追跡することが可能になります。

DFT計算の設定

DFT計算を設定する際は、PySCFの dft.RKS クラスを活用します。このクラスは、制限付きKohn-Sham DFT計算を行うためのメソッドを提供しており、計算中に生成されるデータをチェックポイントファイルに保存する機能もあります。以下のコードは、基本的な設定を示しています。

from pyscf import dft

mf = dft.RKS(mol)  # 分子オブジェクトをRKSクラスに渡す
mf.chkfile = path + '.chk'  # 計算のチェックポイントファイルの保存先
mf.xc = 'B3LYP'  # 交換相関汎関数としてB3LYPを使用
mf.max_cycle = 150  # SCF計算の最大反復回数



詳細説明:

• mf = dft.RKS(mol): このコマンドは、mol で指定された分子に対して、制限付きKohn-Sham DFT計算を行う準備をします。
• mf.chkfile: 計算過程で得られるデータを保存するファイルのパスを指定します。これにより、計算が中断された場合でも、途中から再開することが可能になります。
• mf.xc: 交換相関汎関数を指定します。B3LYP は広く使用されるハイブリッド汎関数の一つで、良好な精度と計算コストのバランスを提供します。
• mf.max_cycle: 自己無撞着場（SCF）計算の最大反復回数を指定します。150回という設定は、多くの場合において収束に十分な反復回数を提供しますが、計算の難易度や分子の大きさによっては調整が必要な場合もあります。

この設定により、DFT計算の基本的なフレームワークが構築され、エネルギー最小化や他の電子構造計算に移行する準備が整います。

エネルギーと構造の収集

計算中のエネルギーと構造を記録するために、リストを初期化します。これにより、最適化の各ステップでの分子のエネルギーと構造データを追跡できます。

energies = []  # 各ステップのエネルギーを保存するリスト
geometries = []  # 各ステップの分子構造を保存するリスト

コールバック関数の定義

最適化プロセス中に特定の計算情報をキャプチャするためのコールバック関数cbを定義します。この関数は各ステップのエネルギーと構造をリストに追加し、さらに詳細な分析情報を提供します。

def cb(envs):
    mf = envs['g_scanner'].base  # 現在の計算オブジェクトを取得
    energies.append(mf.e_tot)  # エネルギーをリストに追加
    geometries.append(mol.atom_coords(unit="ANG"))  # ジオメトリーをリストに追加



収束条件の設定

最適化の収束条件を定義します。これにより、エネルギーと構造の変化が指定された閾値以下になるまで計算が続行されます。この収束設定はGaussianのデフォルトに近い設定値にしています。

conv_params = {
    'convergence_energy': 1e-6,  # エネルギーの収束閾値 (Eh)
    'convergence_grms': 3e-4,    # 勾配のRMS収束閾値 (Eh/Bohr)
    'convergence_gmax': 4.5e-4,  # 最大勾配の収束閾値 (Eh/Bohr)
    'convergence_drms': 1.2e-3,  # 変位のRMS収束閾値 (Angstrom)
    'convergence_dmax': 1.8e-3   # 最大変位の収束閾値 (Angstrom)
}


構造最適化の実行

このセクションでは、PySCFを用いて分子の構造最適化を行い、その過程で得られたエネルギーとジオメトリーのデータをプロットおよび保存する手順を説明します。以下のコードでは、geometric_solver を使用して構造最適化を行い、その結果を可視化およびファイルに出力しています。

from pyscf.geomopt import geometric_solver
import matplotlib.pyplot as plt
import sys

# 構造最適化を実行
geometric_solver.optimize(mf, callback=cb, **conv_params)

# エネルギー収束のプロット
plt.figure(figsize=(10, 5))
plt.plot(energies, marker='o')
plt.title('Energy Convergence During Geometry Optimization')
plt.xlabel('Optimization Step')
plt.ylabel('Total Energy (Hartree)')
plt.grid(True)
plt.show()

# ジオメトリーの保存
for i, coords in enumerate(geometries):
    filename = f"{path}_geometry_step_{i+1}.xyz"
    with open(filename, 'w') as f:
        f.write(f"{mol.natm}\\\\n")
        f.write(f"Step {i+1} Energy: {energies[i]}\\\\n")
        for j in range(mol.natm):
            symbol = mol.atom_pure_symbol(j)
            x, y, z = coords[j]
            f.write(f"{symbol} {x:.6f} {y:.6f} {z:.6f}\\\\n")

print("All geometries have been saved.")



説明

• 構造最適化: geometric_solver.optimize メソッドを使用して、分子の構造をエネルギーが最小となる形に最適化します。ここで、callback 関数が各最適化ステップで呼び出され、エネルギーとジオメトリーが収集されます。
• エネルギー収束のプロット: 最適化過程でのエネルギー変化をプロットします。これにより、最適化の進行と収束を視覚的に確認することができます。
• ジオメトリーの保存: 各最適化ステップのジオメトリーをXYZフォーマットでファイルに保存します。ファイル名はステップ数と結合して生成され、各ステップでのエネルギーも記載されます。

このコードにより、分子の構造最適化が実行され、その結果が詳細に記録されます。このプロセスは、Google ColabのCPUを使用する場合、約2分で完了する見込みです。

実行結果の確認

以下のようにエネルギーが収束しているグラフが得られます。また、設定したパスに構造情報がXYZファイルとして保存されていることを確認してください。

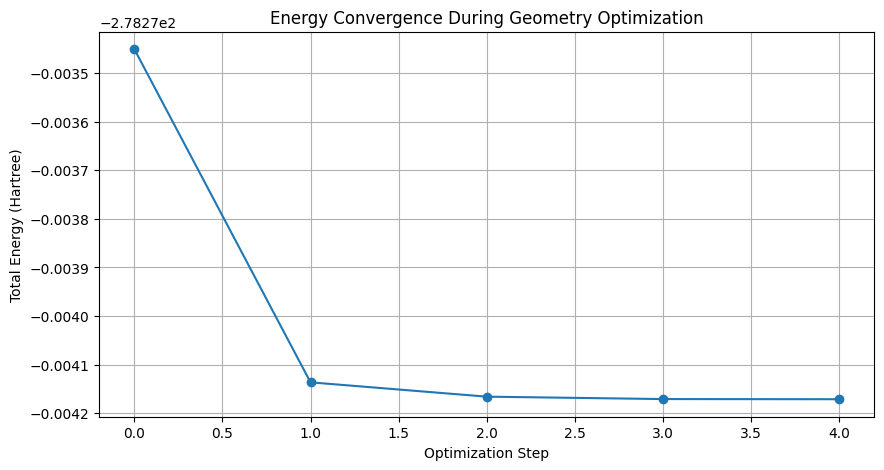
エネルギーの収束プロセスをグラフで確認することは、構造最適化が適切に行われたかを理解する上で重要です。XYZファイルに保存されたジオメトリー情報を通じて、各最適化ステップでの分子の形状変化も詳細に追跡することができます。

計算が途中で停止した場合の対処法

Google Colabの無料版を使用している場合、特に操作を行わない状態が続くと、ランタイムが約90分後に自動的に切断されてしまいます。計算がこのように途中で終了してしまった場合は、保存されたチェックポイントファイルを利用して計算を再開することができます。

チェックポイントファイルからの計算再開: チェックポイントファイルから分子構造を読み込み、その構造を使用して構造最適化計算を再開します。このステップでは、lib.chkfile.load_mol 関数を使用して保存された分子構造をロードし、構造最適化を続行します。分子の定義を以下のコードに置き換えて下さい。

from pyscf import lib, gto

mol = lib.chkfile.load_mol(path + '.chk')


実行する前に必ず、これまで解説した構造最適化計算を行う手順と同様に、必要なライブラリのインストール、Googleドライブのマウント、パスの設定などを行ってください。すべての設定が完了したら、PySCFの計算を再度実行して構造最適化を完了させます。

これらの手順により、途中で停止した計算をスムーズに再開し、計画していた構造最適化を完了させることが可能です。この方法は計算途中のデータを失わないため、時間とリソースの節約にもつながります。

分子構造の可視化

分子構造の可視化には、Pythonの py3Dmol ライブラリが特に便利です。このライブラリを活用することで、Google Colab上で3Dでインタラクティブな分子モデルを簡単に表示できます。

py3Dmolとは？

py3Dmol は、分子の3D可視化をサポートするPythonライブラリで、Webベースの3Dmol.jsの機能をPython環境内で利用できるようにします。このツールは科学研究や教育で広く使われており、XYZファイルやPDBファイルなど、様々な形式の分子データを読み込んで可視化することが可能です。

可視化の実装

以下のコードを用いて、構造最適化で得られた各ステップの分子構造を可視化します。特に最後のステップのXYZファイルを読み込み、それを py3Dmol で表示します。

import ipywidgets
from ipywidgets import interact
import py3Dmol

# モデルのXYZ座標をファイルから読み込む
def read_xyz(file_path):
    with open(file_path, 'r') as file:
        return file.read()

# py3Dmolでのビューアを設定する関数
def show_structure(xyz_content, style):
    view = py3Dmol.view(width=800, height=400)
    view.addModel(xyz_content, 'xyz')
    if style == 'ball and stick':
        view.setStyle({'stick':{}, 'sphere':{'radius': 0.5}})
    elif style == 'stick':
        view.setStyle({'stick': {}})
    elif style == 'line':
        view.setStyle({'line': {'linewidth': 5}})
    elif style == 'sphere':
        view.setStyle({'sphere': {}})
    view.setBackgroundColor('white')
    view.zoomTo()
    return view.show()

# ファイルパスを設定
filename_template = f"{path}_geometry_step_"

# 最適化ステップの数に応じたインタラクション
def style_selector(idx, s):
    filename = f"{filename_template}{idx}.xyz"
    xyz_content = read_xyz(filename)
    show_structure(xyz_content, s)

# インタラクションウィジェットの設定
max_steps = i + 1  # 最適化ステップの総数
interact(style_selector, 
         idx=ipywidgets.IntSlider(min=1, max=max_steps, step=1, value=max_steps, description='Step'),
         s=ipywidgets.Dropdown(
             options=['ball and stick', 'stick','line', 'sphere'],
             value='ball and stick',
             description='Style:'))



ビューアーのスタイル設定

setStyle メソッドを用いて分子の表示スタイルをカスタマイズできます。画像左上のStyleのプルダウンではスティックモデル、スフィアモデル、ラインモデルを選択することができます。その上のStepを変えることで、構造最適化が進行する様子を視覚的に追跡することができます。

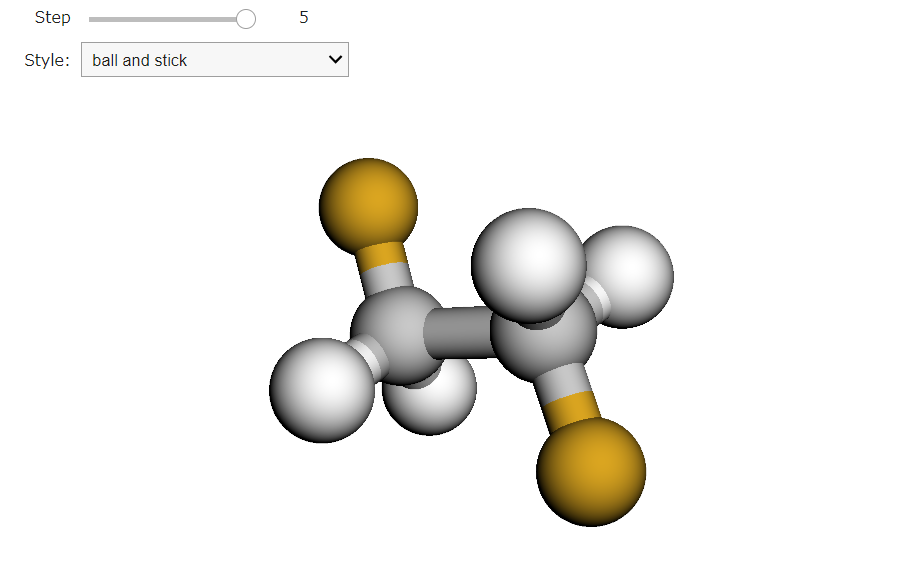
振動数計算と構造最適化計算を組み合わせて行う理由

構造最適化計算によって分子のエネルギーを最小化し、原子の配置を調整することは、分子の安定構造を見つける基本的なアプローチです。**しかし、構造最適化計算だけでは、得られた構造が真に安定（基底状態）かどうかを確認することはできません。**これは、構造がエネルギーの局所的な最小値（局所ミニマムまたは鞍点）に落ち着く可能性があるためです。

分子の振動数計算は、構造最適化後の構造が真のエネルギー最小値にあるかどうかを判定するために非常に重要です。振動数計算を通じて、分子の振動モードが全て正の値を持つ場合、その構造は安定な最小エネルギー状態（真の最小値）にあると判断されます。もし一つでも負の振動数が見つかる場合（虚振動が存在する場合）、それは構造が鞍点にあることを意味し、分子が不安定である可能性があります。

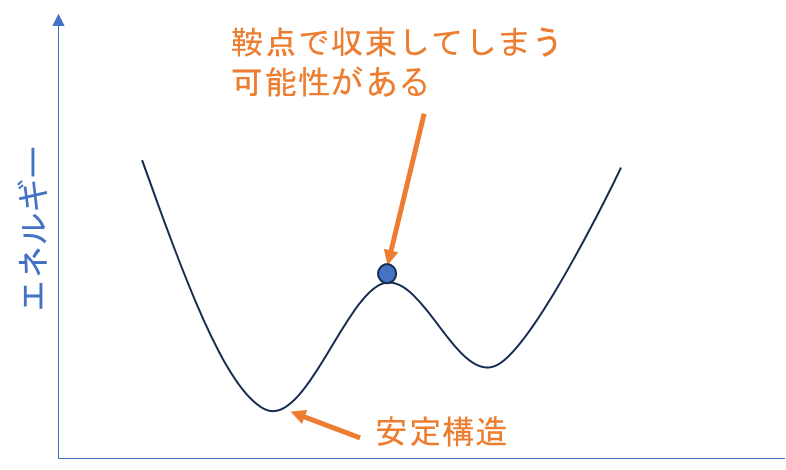
分子のポテンシャル局面 ※参考文献[9]

振動数計算の実行

今回は、構造最適化で得られたデータを使用して振動数計算を行います。計算の所要時間は約2分です。

from pyscf import dft, lib
from pyscf.hessian import rks, thermo

# チェックポイントファイルから分子構造を読み込み
mol = lib.chkfile.load_mol(path + '.chk')

# DFT計算の設定
mf = dft.RKS(mol)
mf.chkfile = path + '.chk'
mf.xc = 'B3LYP'

# DFT計算を実行
mf.kernel()

# 振動数計算のためのHessianオブジェクトを生成
hessian = rks.Hessian(mf)

# 振動数計算を実行
freqs = hessian.kernel()
freq_info = thermo.harmonic_analysis(mf.mol, freqs)

# 振動数計算の結果を表示する関数
def display_vibrational_frequencies(freq_info):
    """
    振動数計算の結果を確認し、表示します。
    """
    if freq_info['freq_error'] == 0:
        print("振動数計算は正常に完了しました。")
    else:
        print("振動数計算結果に虚振動がありました。")

    print("振動数の結果:")
    print("{:>10} {:>10} {:>15}".format("Index", "Freq (cm^-1)", "Type"))
    for i, (freq, wavenumber) in enumerate(zip(freq_info['freq_au'], freq_info['freq_wavenumber'])):
        freq_type = "Real" if freq > 0 else "Imaginary"
        print("{:>10} {:>10.2f} {:>15}".format(i + 1, wavenumber, freq_type))

# 結果を表示
display_vibrational_frequencies(freq_info)



実行結果の説明

このコードを実行すると、以下のような振動数の計算結果が出力されます。すべての振動数が実数（”Real”）であれば、振動数計算は正常に完了しました。と表示され、分子はエネルギー的に安定な最小エネルギー状態にあります。もし虚数の振動数（”Imaginary”）があれば、その構造が鞍点であることを示唆しています。

振動数計算は正常に完了しました。
振動数の結果:
Index Freq (cm^-1)            Type
1     129.68            Real
2     274.37            Real
3     458.21            Real
4     824.03            Real
5    1084.74            Real
6    1087.49            Real
7    1098.10            Real
8    1191.03            Real
9    1240.03            Real
10    1312.05            Real
11    1381.72            Real
12    1479.16            Real
13    1549.20            Real
14    1560.65            Real
15    3061.07            Real
16    3066.80            Real
17    3101.49            Real
18    3127.23            Real


この振動数計算により、構造最適化が正しく行われたかを確認し、分子の安定構造についての重要な洞察を得ることができます。

終わりに

いかがでしたでしょうか。PySCFはGoogle colab上で構造最適化が出来るため、非常に手軽に計算することが出来ます。さらに、有料版などを使うと自宅PCではできないような大きな分子も計算可能です。是非気軽に試してみてください！

参考文献

Gaussianを使った量子化学計算の初心者向け技術書を販売中

¥2,000 → ¥1,000 今なら50%OFF!!

しばしば出くわすエラーへの対処法をはじめ
Gaussianと無料ソフトウェア Avogadro を組み合わせた物性解析手法が学べます！

技術書ページへ