この記事では、タンパク質-ペプチド複合体(ColabFold等で予測した構造)を用いて、GROMACSでMDシミュレーションを行う方法を解説します。コピペでできるようにしているので、ぜひチャレンジしてみてください!
【この記事のまとめ】
In silico創薬に取り組む研究者や学生が、ColabFold等で予測したタンパク質-ペプチド複合体を用いて、GROMACSで分子動力学(MD)シミュレーションを実行する全工程を習得できます。
- 予測構造の欠損修復: PDBFixerを用いて予測構造にありがちな側鎖の欠損原子を自動補完し、AMBER99SB-ILDN力場とTIP3P水モデルを適用する前処理手順を詳説。
- システムの構築と中性化: シミュレーションボックス内への水分子の充填(溶媒和)と、0.15 M NaClによる系の電気的中性化を行う具体的なフローを提示。
- 安定化から本番実行まで: エネルギー最小化(EM)、温度(NVT)・圧力(NPT)の平衡化を経て、10 nsの本番MDを実行するための設定ファイル(mdp)とコマンドを網羅。
読者が得られるメリット:予測された静止構造の不完全さを解消し、信頼性の高いシミュレーション環境でペプチドとタンパク質の相互作用を動的に解析する実践的な技術が身につきます。
Windows 11 Home, 13th Gen Intel(R) Core(TM) i7-13700,
64 ビット オペレーティング システム、x64 ベース プロセッサ, メモリ:32GB
WSL2 (Ubuntu) GPU:NVIDIA GeForce RTX 4070
自宅でできるin silico創薬の技術書を販売中
新薬探索を試したい方必読!
ITエンジニアである著者の視点から、wetな研究者からもdryの創薬研究をわかりやすく身近に感じられるように解説しています
自宅でできるin silico創薬の技術書を販売中
タンパク質デザイン・モデリングに焦点を当て、初めてこの分野に参入する方向けに、それぞれの手法の説明から、環境構築、実際の使い方まで網羅!
環境構築
環境構築はこちらを参考にしてください。
初めての方はこちらの第15章 MD simulationを用いたタンパク質の安定化でMDにいったん慣れた方がスムーズになるかと思います。
MDの実行
1.コードの流れ
このコードは、タンパク質-ペプチド複合体の分子動力学(MD)シミュレーションを行うための一連の準備と実行の手順です。ColabFoldなどで予測した構造はしばしば側鎖が不完全なため、PDBFixerでの修復が重要です。
全体は大きく4つのフェーズに分けられます。
- 初期構造の準備: PDBFixerでPDBファイルの欠損原子を補完し、GROMACS形式に変換し、シミュレーション空間(ボックス)を準備します。
- システム構築: ボックス内に水を充填して溶媒和を行い、イオンを追加して系を電気的に中性にします。
- システムの安定化(平衡化): システムの構造的な不安定性を解消する**エネルギー最小化(EM)**を行い、さらに温度(NVT)と圧力(NPT)を安定化させます。
- 本番MDの実行: 安定化されたシステムで、実際に分子の動きを追跡するメインのシミュレーションを実行します。
今回は以下の記事で生成した環状ペプチドのMDを行ってみます。
【環状ペプチド】Bolzgenを使ったDe novo環状ペプチドの生成【In silico創薬】 – LabCode
以下のfinal_2_designの中にあるPDBファイルをProtein_Peptide.pdb とした後にコードを実行してください。
2.コードの全体
mdpファイルが適宜必要なので、先に4.mdpファイルを作成してみてください。
# === 0. 環境のアクティベート ===
eval "$(micromamba shell hook --shell bash)"
micromamba activate gromacs_env
# === 1. 初期構造の準備 (PDBFixer と GROMACSでの前処理) ===
# PDBFixerを実行し、欠損アトム(特に側鎖)を補完
pdbfixer Protein_Peptide.pdb --add-atoms=all --add-residues --output=fixed_complex.pdb
# 修正済みのPDBをGROMACS形式に変換(力場と水モデルを指定)
gmx_mpi pdb2gmx -f fixed_complex.pdb -o complex.gro -p topol.top -ignh -ff amber99sb-ildn -water tip3p
# 構造をシミュレーションボックスの中心に配置(1.0 nm余裕)
gmx_mpi editconf -f complex.gro -o boxed.gro -c -d 1.0 -bt cubic
# === 2. システム構築 (水・イオンの追加) ===
# 水分子を充填
gmx_mpi solvate -cp boxed.gro -cs spc216.gro -o solvated.gro -p topol.top
# イオン追加のための実行ファイルを生成
gmx_mpi grompp -f ions.mdp -c solvated.gro -p topol.top -o ions.tpr
# イオンを追加して系を中和(0.15 M NaCl)
echo "13" | gmx_mpi genion -s ions.tpr -o ionized.gro -p topol.top -pname NA -nname CL -neutral -conc 0.15
# === 3. システムの安定化(エネルギー最小化と平衡化) ===
# [エネルギー最小化 (EM)]
gmx_mpi grompp -f em.mdp -c ionized.gro -p topol.top -o em.tpr
gmx_mpi mdrun -v -deffnm em
# インデックスファイルの作成(温度カップリンググループ用)
# ここでは選んだ1|2で1(タンパク質)と同じものが作られます。一見意味なさそうですが、index.ndxファイルがあると楽なので、いったんここで作成しています。
echo -e "1 | 2\nq" | gmx_mpi make_ndx -f em.gro -o index.ndx
# [NVT平衡化(温度一定)]
gmx_mpi grompp -f nvt.mdp -c em.gro -r em.gro -p topol.top -n index.ndx -o nvt.tpr
gmx_mpi mdrun -v -deffnm nvt
# [NPT平衡化(圧力一定)]
gmx_mpi grompp -f npt.mdp -c nvt.gro -r nvt.gro -t nvt.cpt -p topol.top -n index.ndx -o npt.tpr
gmx_mpi mdrun -v -deffnm npt
# === 4. 本番MDの実行 ===
# 本番MDのための実行ファイルを生成
gmx_mpi grompp -f md.mdp -c npt.gro -t npt.cpt -p topol.top -n index.ndx -o md.tpr
# 本番の分子動力学シミュレーションを実行(バックグラウンド実行推奨)
nohup gmx_mpi mdrun -deffnm md > md.log 2>&1 &3.コードの詳細説明
1. 初期構造の準備(PDBFixerとGROMACSでの前処理)
ColabFoldなどで予測された構造は、側鎖の一部が欠損していることがあります(例:LYSのCD, CE, NZ原子など)。この段階でこれらを修復します。
pdbfixer Protein_Peptide.pdb --add-atoms=all --add-residues --output=fixed_complex.pdb◦pdbfixerはOpenMMに付属するツールで、欠損している原子や残基を自動で補完します。-add-atoms=allオプションで全ての欠損原子を追加します。gmx_mpi pdb2gmx -f fixed_complex.pdb -o complex.gro -p topol.top -ignh -ff amber99sb-ildn -water tip3p◦ GROMACSの**pdb2gmxコマンドで、PDBファイルをGROMACS形式(.gro)に変換します。 ◦ff amber99sb-ildnでAMBER99SB-ILDN力場を指定し、water tip3pでTIP3P水モデル**を使用します。 ◦ignhオプションで既存の水素原子を無視し、力場に従って再構築します。 ◦ マルチチェーン(タンパク質+ペプチド)の場合、各チェーンごとにトポロジーファイル(topol_Protein_chain_A.itp,topol_Protein_chain_B.itp)が生成されます。gmx_mpi editconf -f complex.gro -o boxed.gro -c -d 1.0 -bt cubic◦ シミュレーションボックスを設定します。d 1.0で分子端からボックス境界まで1.0 nmの余裕を持たせます。
2. システム構築(水・イオンの追加)
gmx_mpi solvate -cp boxed.gro -cs spc216.gro -o solvated.gro -p topol.top◦ ボックス内を水分子で充填します(溶媒和)。topol.topに水分子数が自動追記されます。gmx_mpi grompp -f ions.mdp -c solvated.gro -p topol.top -o ions.tpr◦ イオン追加のための実行ファイルを生成します。echo "13" | gmx_mpi genion -s ions.tpr -o ionized.gro -p topol.top -pname NA -nname CL -neutral -conc 0.15◦ **gmx genion**で系を電気的に中和し、生理的塩濃度(0.15 M NaCl)になるようイオンを追加します。 ◦echo "13"は水分子グループ(SOL)を選択するための入力です。
3. システムの安定化(エネルギー最小化と平衡化)
- エネルギー最小化(EM)◦ 原子間の不自然な近接や角度を解消し、安定した出発構造を得ます。 ◦ 収束条件:最大力 < 1000 kJ/mol/nm
- NVT平衡化(100 ps)◦ 温度を300 Kに安定化させます。
◦ タンパク質に位置拘束(
DPOSRES)を適用して構造を維持します。 - NPT平衡化(100 ps)◦ 圧力を1 barに安定化させ、系の密度を調整します。 ◦ C-rescale圧力カップリングを使用します(位置拘束との組み合わせで安定)。
4. 本番MDの実行
- 10 nsのシミュレーションを実行します。
•
nohup ... &でバックグラウンド実行すれば、ターミナルを閉じても継続します。
4.mdpファイル
以下のmdpファイルを作成してください。
ions.mdp
; ions.mdp - used for adding ions
integrator = steep
emtol = 1000.0
emstep = 0.01
nsteps = 50000
nstlist = 1
cutoff-scheme = Verlet
ns_type = grid
coulombtype = cutoff
rcoulomb = 1.0
rvdw = 1.0
pbc = xyzem.mdp
; em.mdp - Energy Minimization
integrator = steep
emtol = 1000.0
emstep = 0.01
nsteps = 50000
nstlist = 1
cutoff-scheme = Verlet
ns_type = grid
coulombtype = PME
rcoulomb = 1.0
rvdw = 1.0
pbc = xyznvt.mdp
; nvt.mdp - NVT equilibration
define = -DPOSRES
integrator = md
nsteps = 50000 ; 100 ps
dt = 0.002
nstxout = 500
nstvout = 500
nstenergy = 500
nstlog = 500
continuation = no
constraint_algorithm = lincs
constraints = h-bonds
lincs_iter = 1
lincs_order = 4
cutoff-scheme = Verlet
ns_type = grid
nstlist = 10
rcoulomb = 1.0
rvdw = 1.0
coulombtype = PME
pme_order = 4
fourierspacing = 0.16
tcoupl = V-rescale
tc-grps = Protein Non-Protein
tau_t = 0.1 0.1
ref_t = 300 300
pcoupl = no
pbc = xyz
gen_vel = yes
gen_temp = 300
gen_seed = -1npt.mdp
; npt.mdp - NPT equilibration
define = -DPOSRES
integrator = md
nsteps = 50000 ; 100 ps
dt = 0.002
nstxout = 500
nstvout = 500
nstenergy = 500
nstlog = 500
continuation = yes
constraint_algorithm = lincs
constraints = h-bonds
lincs_iter = 1
lincs_order = 4
cutoff-scheme = Verlet
ns_type = grid
nstlist = 10
rcoulomb = 1.0
rvdw = 1.0
coulombtype = PME
pme_order = 4
fourierspacing = 0.16
tcoupl = V-rescale
tc-grps = Protein Non-Protein
tau_t = 0.1 0.1
ref_t = 300 300
pcoupl = C-rescale
pcoupltype = isotropic
tau_p = 2.0
ref_p = 1.0
compressibility = 4.5e-5
refcoord_scaling = com
pbc = xyz
gen_vel = nomd.mdp
長さを変更したい場合は、nsteps = 5000000 ; 10 nsの部分を変更してみてください。
; md.mdp - Production MD (10 ns)
integrator = md
nsteps = 5000000 ; 10 ns
dt = 0.002
nstxout = 0
nstvout = 0
nstfout = 0
nstenergy = 5000
nstlog = 5000
nstxout-compressed = 5000
compressed-x-grps = System
continuation = yes
constraint_algorithm = lincs
constraints = h-bonds
lincs_iter = 1
lincs_order = 4
cutoff-scheme = Verlet
ns_type = grid
nstlist = 10
rcoulomb = 1.0
rvdw = 1.0
coulombtype = PME
pme_order = 4
fourierspacing = 0.16
tcoupl = V-rescale
tc-grps = Protein Non-Protein
tau_t = 0.1 0.1
ref_t = 300 300
pcoupl = Parrinello-Rahman
pcoupltype = isotropic
tau_p = 2.0
ref_p = 1.0
compressibility = 4.5e-5
pbc = xyz
DispCorr = EnerPres
gen_vel = no5.生成されるファイル一覧
| ステップ | 出力ファイル | 説明 |
|---|---|---|
| PDB修復 | fixed_complex.pdb | 欠損原子を補完したPDB |
| pdb2gmx | complex.gro, topol.top, topol_Protein_chain_*.itp, posre_Protein_chain_*.itp | 構造・トポロジー・位置拘束 |
| editconf | boxed.gro | ボックス設定済み構造 |
| solvate | solvated.gro | 水分子追加済み |
| genion | ionized.gro | イオン追加済み |
| EM | em.gro, em.edr, em.log | エネルギー最小化後の構造 |
| make_ndx | index.ndx | インデックスファイル |
| NVT | nvt.gro, nvt.cpt, nvt.edr | NVT平衡化後 |
| NPT | npt.gro, npt.cpt, npt.edr | NPT平衡化後 |
| MD | md.xtc, md.edr, md.log | 本番トラジェクトリ |
後処理
MDシミュレーション後、解析・可視化のためにトラジェクトリのPBC(周期的境界条件)補正を行います。シミュレーション中にタンパク質がボックス境界を越えて「ジャンプ」したり、分子が分断されて見えるアーティファクトを除去します。
1. 後処理の流れ
後処理は以下の3段階で行います。1回のtrjconv呼び出しで全てを処理することはできないため、段階的に処理します。
- 分子のwhole化: PBC境界で分断された分子を修復する
- センタリング: タンパク質をボックスの中心に配置し、PBCアーティファクトを除去する
- フィッティング: タンパク質の回転・並進を除去し、初期構造に重ね合わせる
2. 後処理コマンド
# === 0. 環境のアクティベート ===
eval "$(micromamba shell hook --shell bash)"
micromamba activate gromacs_env
# === 1. 分子をwhole(完全な形)にする ===
# PBC境界で分断された分子を修復する
# 入力: 0 (System) を出力グループとして選択
printf "0\n" > /tmp/gmx_input.txt
gmx_mpi trjconv -s md.tpr -f md.xtc -o md_whole.xtc -pbc whole -n index.ndx < /tmp/gmx_input.txt
# === 2. タンパク質をボックス中央に配置 ===
# 入力: 1 (Protein) でセンタリング、0 (System) を出力
printf "1\n0\n" > /tmp/gmx_input.txt
gmx_mpi trjconv -s md.tpr -f md_whole.xtc -o md_center.xtc -center -pbc mol -ur compact -n index.ndx < /tmp/gmx_input.txt
# === 3. 回転・並進のフィッティング ===
# 入力: 1 (Protein) でフィッティング、0 (System) を出力
printf "1\n0\n" > /tmp/gmx_input.txt
gmx_mpi trjconv -s md.tpr -f md_center.xtc -o md_fit.xtc -fit rot+trans -n index.ndx < /tmp/gmx_input.txt
# === 4. 中間ファイルの削除 ===
rm -f md_whole.xtc md_center.xtc
# === 5. 最終構造(GRO)のPBC補正(可視化用) ===
printf "1\n0\n" > /tmp/gmx_input.txt
gmx_mpi trjconv -s md.tpr -f md.gro -o md_final.gro -center -pbc mol -ur compact -n index.ndx < /tmp/gmx_input.txt3. 各コマンドの詳細説明
Step 1: -pbc whole
シミュレーション中に分子がPBC境界をまたいで分断されることがあります。-pbc wholeは、分子の結合情報(トポロジー)を基に、分断された分子を1つのまとまりとして復元します。
Step 2: -center -pbc mol -ur compact
center:指定したグループ(Protein)をボックスの中心に再配置します。pbc mol:各分子をユニットセル内に「ラップ」し、分子がボックス境界を越えて見えるのを防ぎます。ur compact:出力されるユニットセルの表現をコンパクト(菱形十二面体に近い形)にします。
Step 3: -fit rot+trans
タンパク質の回転と並進を除去し、リファレンス構造(tprファイルの初期構造)に最小二乗フィッティングします。これにより、RMSD解析やトラジェクトリの可視化が容易になります。
Step 5: 最終構造の補正
md.gro(最終フレームの構造)に対しても同様のセンタリング処理を行い、PyMOLやVMDでの可視化に適したクリーンな構造ファイルmd_final.groを生成します。
Note: MPI版GROMACS(
gmx_mpi)はパイプ入力(echo "0" | gmx_mpi ...)が動作しないことがあります。printfでファイルに書き出し、リダイレクト(< /tmp/gmx_input.txt)で入力してください。
4. 生成されるファイル一覧
| ステップ | 出力ファイル | 説明 |
|---|---|---|
| whole化 | md_whole.xtc | 分子修復済み(中間ファイル、削除可) |
| センタリング | md_center.xtc | 中心配置済み(中間ファイル、削除可) |
| フィッティング | md_fit.xtc | 最終解析用トラジェクトリ |
| 最終構造補正 | md_final.gro | 可視化用の最終構造 |
参考
解析
タンパク質-ペプチド複合体のMDシミュレーション解析では、以下の5つの主要な解析を行います。全て後処理済みのmd_fit.xtcを使用します。
0. 解析用インデックスグループの作成
Chain A(タンパク質)とChain B(ペプチド)を分離したインデックスグループを作成します。
# === 環境のアクティベート ===
eval "$(micromamba shell hook --shell bash)"
micromamba activate gromacs_env
# チェーンごとのグループを作成
printf "splitch 1\nname 18 Protein_A\nname 19 Peptide_B\n18 & 4\nname 20 Protein_A_Backbone\n19 & 4\nname 21 Peptide_B_Backbone\n18 & 3\nname 22 Protein_A_Calpha\n19 & 3\nname 23 Peptide_B_Calpha\nq\n" > /tmp/gmx_input.txt
gmx_mpi make_ndx -f md.tpr -n index.ndx -o index.ndx < /tmp/gmx_input.txt| 入力コマンド | 意味 |
|---|---|
splitch 1 | グループ1(Protein)を チェーンごとに分割。Chain AとChain Bが別々のグループ(例: 18, 19)として追加される |
name 18 Protein_A | グループ18に Protein_A という名前をつける |
name 19 Peptide_B | グループ19に Peptide_B という名前をつける |
18 & 4 | グループ18(Protein_A)とグループ4(Backbone)の AND演算(共通部分) → Protein AのBackbone原子のみ抽出 |
name 20 Protein_A_Backbone | 上記で作成されたグループ20に名前をつける |
19 & 4 | グループ19(Peptide_B)とグループ4(Backbone)のAND演算 → Peptide BのBackbone原子のみ抽出 |
name 21 Peptide_B_Backbone | グループ21に名前をつける |
18 & 3 | グループ18(Protein_A)とグループ3(C-alpha)のAND演算 → Protein AのCα原子のみ抽出 |
name 22 Protein_A_Calpha | グループ22に名前をつける |
19 & 3 | グループ19(Peptide_B)とグループ3(C-alpha)のAND演算 → Peptide BのCα原子のみ抽出 |
name 23 Peptide_B_Calpha | グループ23に名前をつける |
q | 保存して終了 |
作成されるグループ:
| グループ番号 | 名前 | 内容 |
|---|---|---|
| 18 | Protein_A | タンパク質(Chain A)全原子 |
| 19 | Peptide_B | ペプチド(Chain B)全原子 |
| 20 | Protein_A_Backbone | タンパク質のバックボーン |
| 21 | Peptide_B_Backbone | ペプチドのバックボーン |
| 22 | Protein_A_Calpha | タンパク質のCα |
| 23 | Peptide_B_Calpha | ペプチドのCα |
1. RMSD解析
RMSD(Root Mean Square Deviation)は、初期構造からの構造変化を定量化します。複合体全体、タンパク質単体、ペプチド単体の3つを算出します。このRMSD値はBackboneを使用していますが、Cαの原子を使うことの方が多い印象です。
# 複合体全体(Backbone)
# fit: 4 (Backbone), RMSD: 4 (Backbone)
printf "4\n4\n" > /tmp/gmx_input.txt
gmx_mpi rms -s md.tpr -f md_fit.xtc -o rmsd_complex.xvg -n index.ndx -tu ns < /tmp/gmx_input.txt
# タンパク質(Chain A Backbone)
# fit: 20 (Protein_A_Backbone), RMSD: 20 (Protein_A_Backbone)
printf "20\n20\n" > /tmp/gmx_input.txt
gmx_mpi rms -s md.tpr -f md_fit.xtc -o rmsd_protein.xvg -n index.ndx -tu ns < /tmp/gmx_input.txt
# ペプチド(Chain B Backbone)
# fit: 21 (Peptide_B_Backbone), RMSD: 21 (Peptide_B_Backbone)
printf "21\n21\n" > /tmp/gmx_input.txt
gmx_mpi rms -s md.tpr -f md_fit.xtc -o rmsd_peptide.xvg -n index.ndx -tu ns < /tmp/gmx_input.txt- RMSDが収束(プラトー到達) → システムが平衡に達したことを示す
- ペプチドのRMSDがタンパク質より大きい → ペプチドがより大きく動いている(結合部位で柔軟に揺らいでいる可能性)
後述のプロットのスクリプトをrunさせると以下のようなグラフがでます。
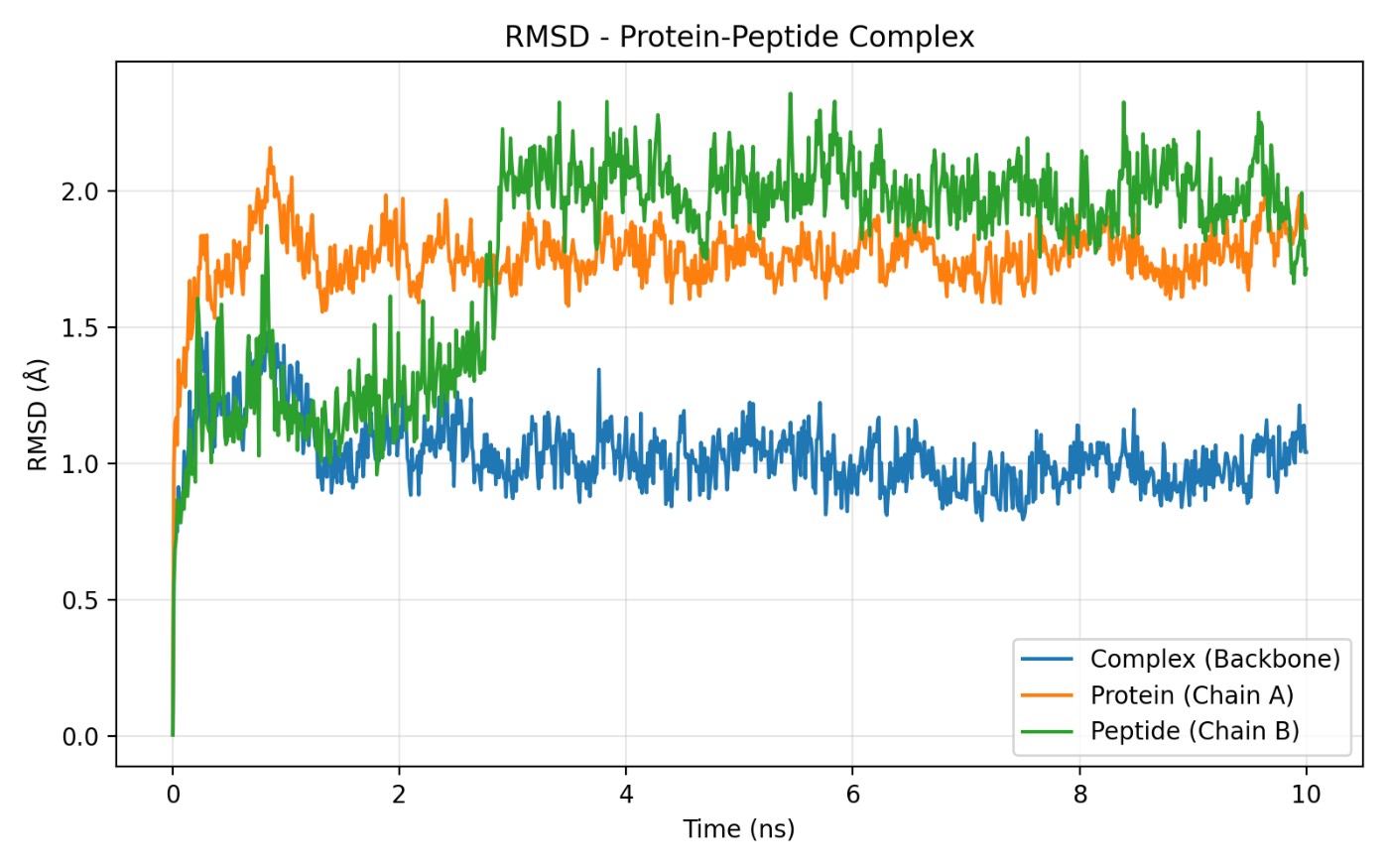
このグラフの見方: 初期構造からどれだけ構造が変化したかを時間で追跡しています。値が小さいほど初期構造に近く、安定しています。
読み取り結果:
- タンパク質(Chain A, オレンジ): 約 0.8〜1.0 Å で安定。最も変動が小さい
- 複合体全体(Backbone, 青): 約 1.0〜1.5 Å で推移
- ペプチド(Chain B, 緑): 約 1.5〜2.2 Å と最も大きく揺らいでいる
解釈: タンパク質は構造が安定している一方、ペプチドはより大きく動いています。これはペプチドがタンパク質表面で柔軟に揺ら いでいることを示します。3つとも開始直後(〜1 ns)に急上昇した後、大きなトレンド変化なく推移しているため、系は概ね平衡に達していると判断できます。
2. RMSF解析
RMSF(Root Mean Square Fluctuation)は、各残基の揺らぎ(柔軟性)を定量化します。
# Cα原子の残基ごとのRMSF
# 3 (C-alpha) を選択
printf "3\n" > /tmp/gmx_input.txt
gmx_mpi rmsf -s md.tpr -f md_fit.xtc -o rmsf_calpha.xvg -n index.ndx -res < /tmp/gmx_input.txt- RMSFが高い残基 → 柔軟性が高い(ループ領域や末端に多い)
- RMSFが低い残基 → 構造が安定(二次構造のコア部分)
- ペプチド結合界面の残基のRMSF → 結合の安定性に関する示唆
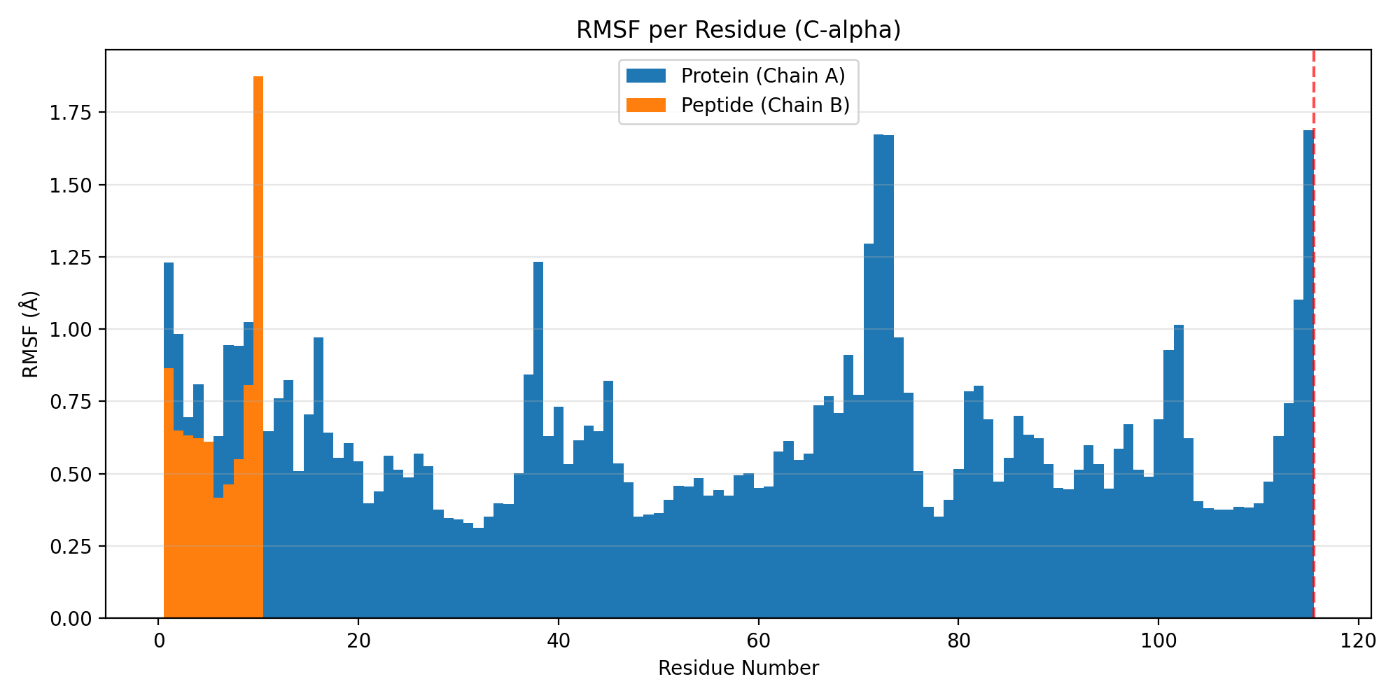
このグラフの見方: 各残基が平均構造からどれだけ揺れたかを棒グラフで示しています。値が高いほどその残基は柔軟に動いています。赤い点線がタンパク質とペプチドの境界です。
読み取り結果:
- タンパク質(青): 大部分が 0.3〜0.8 Å と安定。ただし、残基 70〜75 付近(約 1.3〜1.7 Å)とC末端付近の残基 110〜115(約 1.7 Å)に高いピークがある
- ペプチド(オレンジ): 残基 10 付近で最大約 1.85 Å と非常に高い揺らぎを示す
解釈: タンパク質のコア部分(残基 20、60 付近)は RMSFが低く構造的に安定しています。一方、高ピークの箇所はループ領域や末端で、構造的に自由度が高い部分です。ペプチドは特にC末端側(このペプチドでは相互作用していないアミノ酸)で大きく揺れており、結合部位から離れた末端が溶媒中で自由に動いていると考えられます。
3. 水素結合解析
タンパク質-ペプチド間の水素結合数の時間変化を解析します。
# タンパク質(18)-ペプチド(19)間の水素結合
printf "18\n19\n" > /tmp/gmx_input.txt
gmx_mpi hbond -s md.tpr -f md_fit.xtc -num hbond_protein_peptide.xvg -n index.ndx -tu ns < /tmp/gmx_input.txt水素結合数が安定 → ペプチドがしっかり結合している
水素結合数が減少 → ペプチドが解離傾向にある
水素結合数の揺らぎが大きい → 結合が動的に変化している
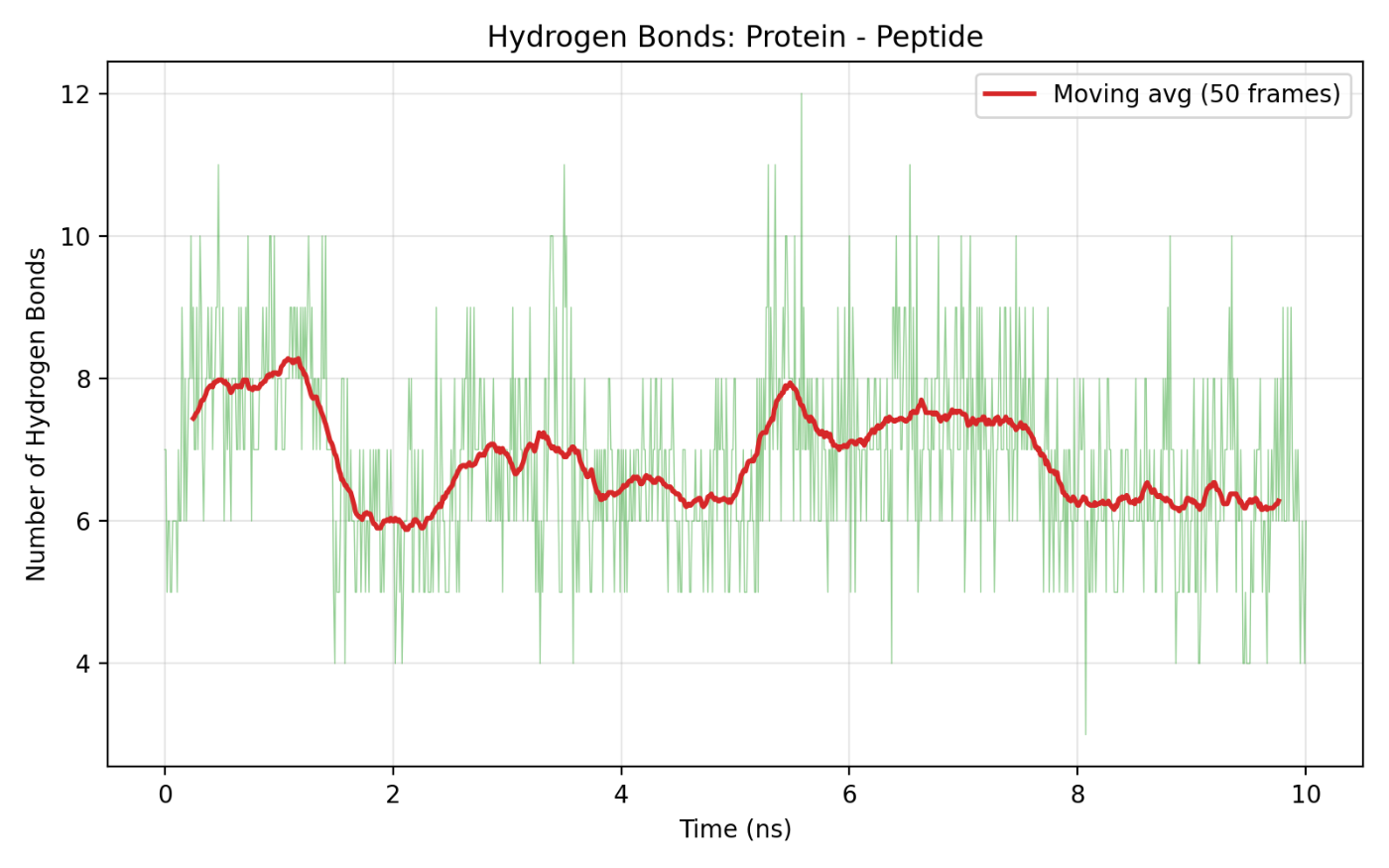
このグラフの見方: タンパク質とペプチドの間に形成されている水素結合の数を時間で追跡しています。赤線は50フレームの移動平均です。
読み取り結果:
- 瞬間値(緑)は約 4〜12 本の間で変動
- 移動平均(赤)は序盤 7〜8 本、後半にかけてやや減少し 6〜7 本程度で推移
解釈: 常に 6〜8 本程度の水素結合が維持されており、ペプチドはタンパク質にしっかり結合した状態を保っていると言えます。水素結合数がゼロに近づいたり急激に減少する様子はないため、シミュレーション中にペプチドが解離する兆候は見られません。ただし後半にかけてわずかに減少傾向があるため、より長い時間スケールでの変化には注意が必要です。
4. 最小距離・コンタクト数解析
タンパク質-ペプチド間の最小原子間距離と、閾値距離(0.4 nm)以内のコンタクト数を解析します。
# 最小距離 (-od) とコンタクト数 (-on)
# 18 (Protein_A), 19 (Peptide_B)
printf "18\n19\n" > /tmp/gmx_input.txt
gmx_mpi mindist -s md.tpr -f md_fit.xtc \ -od mindist_protein_peptide.xvg \ -on numcont_protein_peptide.xvg \ -n index.ndx -tu ns -d 0.4 < /tmp/gmx_input.txt最小距離が常に小さい → ペプチドがタンパク質に密着している
コンタクト数が安定 → 結合界面の接触が維持されている
最小距離が増大 / コンタクト数が減少 → ペプチドの解離を示唆
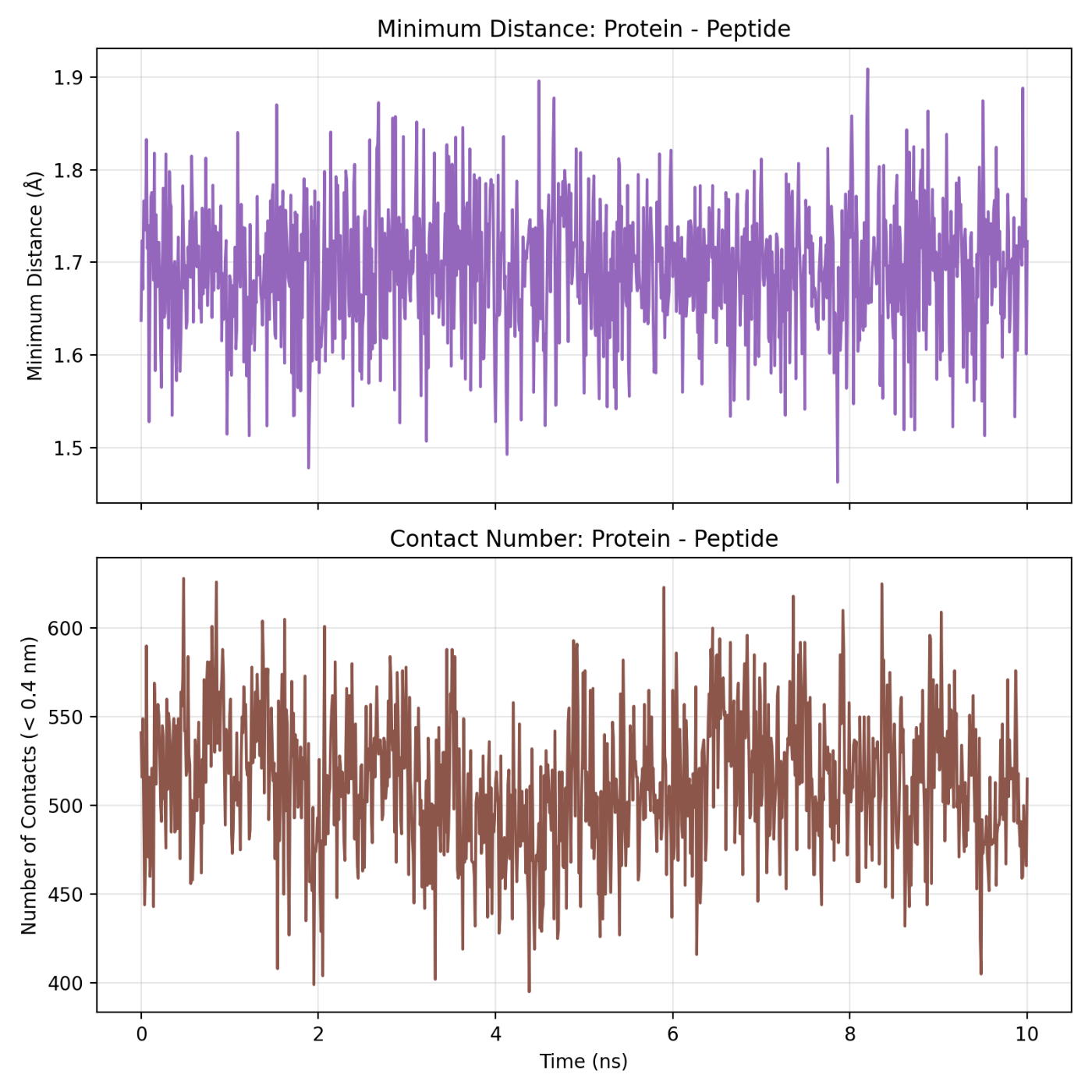
このグラフの見方: 上段はタンパク質-ペプチド間の最も近い原子対の距離、下段は 0.4 nm 以内にある原子対の数(接触数)を示しています。
読み取り結果:
- 最小距離(上段): 約 1.5〜1.9 Å の範囲で安定。大きな離脱なし
- コンタクト数(下段): 約 450〜600 個で変動。中心は約 500 個付近
解釈: 最小距離が常に約 1.7 Å 付近と非常に近く、タンパク質とペプチドが密着した状態が10 ns を通じて維持されていることを示しています。コンタクト数も大きな減少がないため、結合界面は安定です。もし解離が起こっていれば、最小距離が急増しコンタクト数が急減するはずですが、そのような変化は見られません。
5. 回転半径(Rg)解析
回転半径は、複合体全体のコンパクトさを評価します。
# Protein全体 (1) の回転半径
printf "1\n" > /tmp/gmx_input.txt
gmx_mpi gyrate -s md.tpr -f md_fit.xtc -o gyrate.xvg -n index.ndx < /tmp/gmx_input.txtRgが安定 → 複合体の全体構造が維持されている
Rgが増大 → 複合体が広がっている(アンフォールディングや解離の可能性)
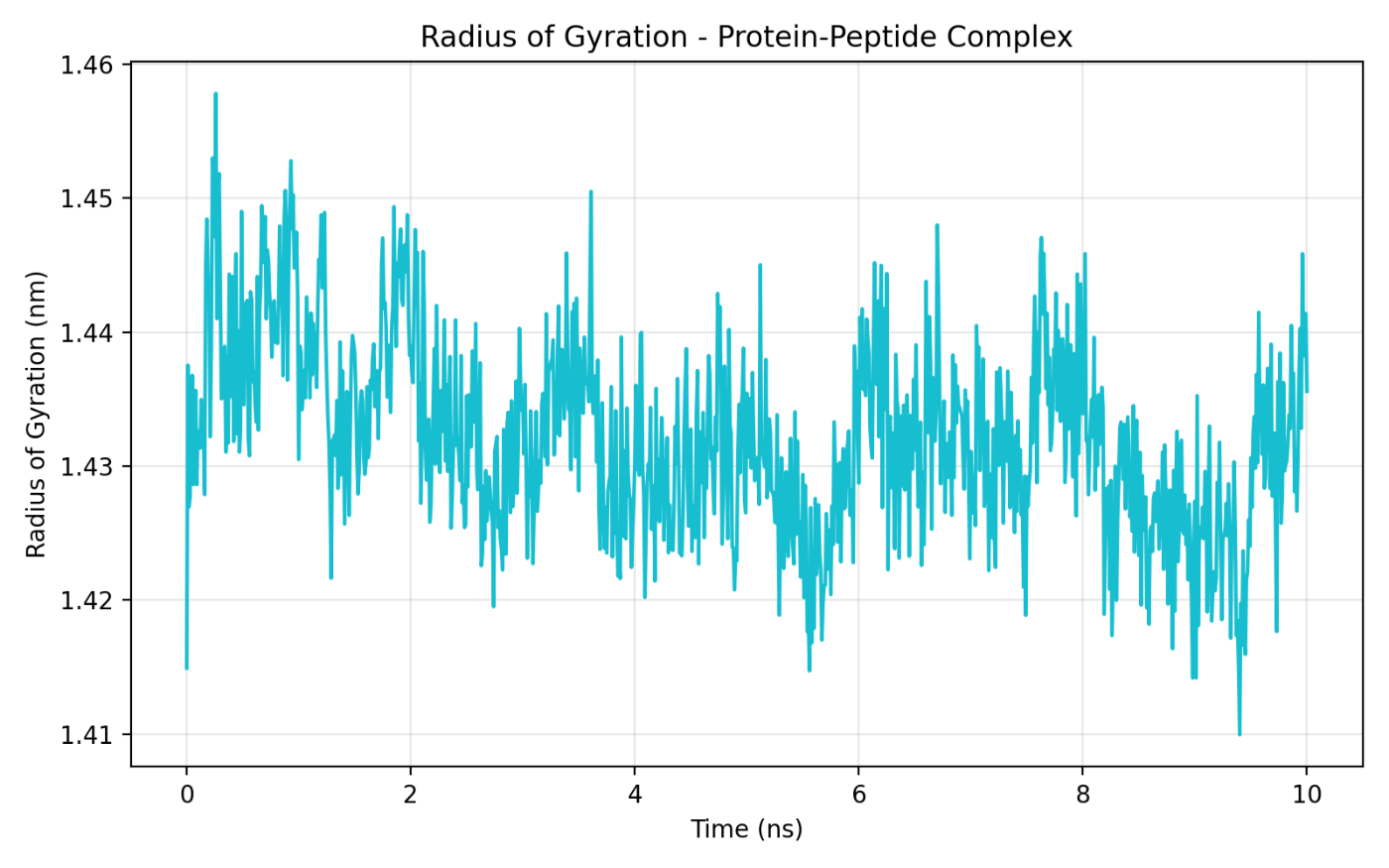
このグラフの見方: 複合体全体のコンパクトさを示す指標です。値が小さいほど構造がコンパクトにまとまっています。
読み取り結果:
- 約 1.41〜1.46 nm の範囲で変動
- 中心値は約 1.43 nm で、大きなトレンド変化なし
解釈: Rg が 10 ns を通じてほぼ一定であり、複合体全体の形状が維持されていることを示します。Rgが時間とともに増大する場合はアンフォールディング(構造のほどけ)や複合体の解離を示唆しますが、今回のシミュレーションではそのような兆候はありません。
6. プロットスクリプト
以下のplot_analysis.pyで全解析結果をプロットします。
#!/usr/bin/env python3
"""
タンパク質-ペプチド複合体 MD解析プロットスクリプト
RMSD, RMSF, 水素結合, 最小距離/コンタクト数, 回転半径 を一括プロット
"""
import re
import numpy as np
import matplotlib.pyplot as plt
def parse_xvg(path): """GROMACS .xvg ファイルを読み込み、データ・メタ情報を返す""" meta = {"title": None, "xlabel": None, "ylabel": None, "legends": []} rows = [] with open(path, "r", encoding="utf-8", errors="ignore") as f: for line in f: s = line.strip() if not s: continue if s.startswith(("@", "#")): m = re.search(r'@.*title\s+"([^"]+)"', s) if m: meta["title"] = m.group(1) m = re.search(r'@.*xaxis\s+label\s+"([^"]+)"', s) if m: meta["xlabel"] = m.group(1) m = re.search(r'@.*yaxis\s+label\s+"([^"]+)"', s) if m: meta["ylabel"] = m.group(1) m = re.search(r'legend\s+"([^"]+)"', s) if m: meta["legends"].append(m.group(1)) continue parts = s.split() if len(parts) >= 2: try: row = [float(p) for p in parts] rows.append(row) except ValueError: pass return np.array(rows), meta
def ps_to_ns(t): """ps を ns に変換(1000以上ならpsと判定)""" if len(t) > 1 and t[-1] > 100: return t / 1000.0 return t
# === 1. RMSD ===
fig, ax = plt.subplots(figsize=(8, 5))
for fname, label in [ ("rmsd_complex.xvg", "Complex (Backbone)"), ("rmsd_protein.xvg", "Protein (Chain A)"), ("rmsd_peptide.xvg", "Peptide (Chain B)"),
]: data, meta = parse_xvg(fname) t = data[:, 0] rmsd_nm = data[:, 1] ax.plot(t, rmsd_nm * 10, label=label) # nm -> Å
ax.set_xlabel("Time (ns)")
ax.set_ylabel("RMSD (Å)")
ax.set_title("RMSD - Protein-Peptide Complex")
ax.legend()
ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.savefig("rmsd_analysis.png", dpi=200)
print("Saved: rmsd_analysis.png")
# === 2. RMSF ===
fig, ax = plt.subplots(figsize=(10, 5))
data, meta = parse_xvg("rmsf_calpha.xvg")
residues = data[:, 0]
rmsf_nm = data[:, 1]
# チェーン境界を特定(残基番号からProteinとPeptideを判別)
# ※ n_protein はシステムに応じて変更してください
n_protein = 115
colors = ["#1f77b4"] * n_protein + ["#ff7f0e"] * (len(residues) - n_protein)
ax.bar(residues, rmsf_nm * 10, color=colors, width=1.0, edgecolor="none") # nm -> Å
ax.axvline(x=residues[n_protein - 1] + 0.5, color="red", linestyle="--", alpha=0.7)
ax.set_xlabel("Residue Number")
ax.set_ylabel("RMSF (Å)")
ax.set_title("RMSF per Residue (C-alpha)")
from matplotlib.patches import Patch
legend_elements = [ Patch(facecolor="#1f77b4", label="Protein (Chain A)"), Patch(facecolor="#ff7f0e", label="Peptide (Chain B)"),
]
ax.legend(handles=legend_elements)
ax.grid(True, alpha=0.3, axis="y")
plt.tight_layout()
plt.savefig("rmsf_analysis.png", dpi=200)
print("Saved: rmsf_analysis.png")
# === 3. 水素結合 ===
fig, ax = plt.subplots(figsize=(8, 5))
data, meta = parse_xvg("hbond_protein_peptide.xvg")
t = data[:, 0]
hbonds = data[:, 1]
ax.plot(t, hbonds, color="#2ca02c", alpha=0.5, linewidth=0.5)
window = 50
if len(hbonds) > window: hb_smooth = np.convolve(hbonds, np.ones(window) / window, mode="valid") t_smooth = t[window // 2 : window // 2 + len(hb_smooth)] ax.plot(t_smooth, hb_smooth, color="#d62728", linewidth=2, label=f"Moving avg ({window} frames)")
ax.set_xlabel("Time (ns)")
ax.set_ylabel("Number of Hydrogen Bonds")
ax.set_title("Hydrogen Bonds: Protein - Peptide")
ax.legend()
ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.savefig("hbond_analysis.png", dpi=200)
print("Saved: hbond_analysis.png")
# === 4. 最小距離 & コンタクト数 ===
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(8, 8), sharex=True)
data_md, _ = parse_xvg("mindist_protein_peptide.xvg")
t_md = data_md[:, 0]
mindist = data_md[:, 1]
ax1.plot(t_md, mindist * 10, color="#9467bd") # nm -> Å
ax1.set_ylabel("Minimum Distance (Å)")
ax1.set_title("Minimum Distance: Protein - Peptide")
ax1.grid(True, alpha=0.3)
data_nc, _ = parse_xvg("numcont_protein_peptide.xvg")
t_nc = data_nc[:, 0]
ncont = data_nc[:, 1]
ax2.plot(t_nc, ncont, color="#8c564b")
ax2.set_xlabel("Time (ns)")
ax2.set_ylabel("Number of Contacts (< 0.4 nm)")
ax2.set_title("Contact Number: Protein - Peptide")
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.savefig("mindist_analysis.png", dpi=200)
print("Saved: mindist_analysis.png")
# === 5. 回転半径 ===
fig, ax = plt.subplots(figsize=(8, 5))
data, meta = parse_xvg("gyrate.xvg")
t = ps_to_ns(data[:, 0])
rg = data[:, 1]
ax.plot(t, rg, color="#17becf")
ax.set_xlabel("Time (ns)")
ax.set_ylabel("Radius of Gyration (nm)")
ax.set_title("Radius of Gyration - Protein-Peptide Complex")
ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.savefig("gyrate_analysis.png", dpi=200)
print("Saved: gyrate_analysis.png")
plt.close("all")
print("\nAll analysis plots generated successfully.")実行:
python plot_analysis.py7. 生成されるファイル一覧
| 解析 | xvgファイル | プロット |
|---|---|---|
| RMSD(複合体) | rmsd_complex.xvg | rmsd_analysis.png |
| RMSD(タンパク質) | rmsd_protein.xvg | |
| RMSD(ペプチド) | rmsd_peptide.xvg | |
| RMSF | rmsf_calpha.xvg | rmsf_analysis.png |
| 水素結合 | hbond_protein_peptide.xvg | hbond_analysis.png |
| 最小距離 | mindist_protein_peptide.xvg | mindist_analysis.png |
| コンタクト数 | numcont_protein_peptide.xvg | |
| 回転半径 | gyrate.xvg | gyrate_analysis.png |
最後に
5つの解析すべてが一貫して、10 ns のシミュレーションを通じてタンパク質-ペプチド複合体は安定に結合を維持していることを示しています。ペプチドはタンパク質より柔軟に動いていますが、水素結合・コンタクト数・最小距離のいずれも解離を示唆する変化はなく、安定した複合体として振る舞っています。
以上タンパク質とペプチドリガンドとのMDでした。今回はMDの長さは10nsですが、状況に応じて変えてみてください。基本的には複合体といえど、タンパク質のみのMDとあまり設定上は大差がなかったので、慣れている人は簡単にできた思います。ぜひいろいろな複合体にMDをやってみてください!
参考
自宅でできるin silico創薬の技術書を販売中
新薬探索を試したい方必読!
ITエンジニアである著者の視点から、wetな研究者からもdryの創薬研究をわかりやすく身近に感じられるように解説しています
自宅でできるin silico創薬の技術書を販売中
タンパク質デザイン・モデリングに焦点を当て、初めてこの分野に参入する方向けに、それぞれの手法の説明から、環境構築、実際の使い方まで網羅!










