振動成分の振幅と周波数が時間とともに変化するデータの解析手法として,短時間フーリエ変換(STFT)を紹介しました。
STFT以外にも,周波数や振幅の時間変化を解析する手法があります。
この記事ではその一つである,ヒルベルト変換を用いた包絡線と瞬時周波数の抽出方法について紹介します。
Pythonのソースコードもすべて掲載しています。
macOS Big Sur, python3.7.9

ヒルベルト変換
ヒルベルト変換
まず,包絡線と瞬時周波数の抽出に必要になるヒルベルト変換 (Hilbert transform) について説明します。
ヒルベルト変換とは,ある関数 $x(t)$ に対して
$$
\mathcal{H}[x](t) = x(t) *\frac{1}{\pi t}= \mathrm{P.V.}\int_{-\infty}^{\infty} x(\tau)\frac{1}{\pi(t-\tau)}\mathrm{d}\tau \tag{1}
$$
と言う式で表される変換のことです。
$*$ は畳み込み積分 (convolution) (掛け算ではない)を表していて,関数 $f(t)$ と $g(t)$ に対して
$$
f(t)*g(t) = \int_{-\infty}^{\infty} f(\tau)g(t-\tau)\mathrm{d}\tau
$$
と定義されます。
$f(t)*g(t)$ は $(f*g)(t)$ と書かれることが多いです。
いずれにせよ,$t$ の関数であることを示します。式(1)の最右辺のP.V. はコーシーの主値積分であることを表しています。
被積分関数が特異点をもち,広義積分となる場合があるため,(しっかりとした)参考書ではこのような書き方を目にする場合がありますが,実用上はさして重要ではありません。
さて,畳み込み積分は,フーリエ空間では掛け算(畳み込み定理)として計算できます。したがって,式(1)の定義に従って計算するのではなく,
- まず,解析対象の信号 $x(t)$ をフーリエ変換し $X(f)$ を計算し,
- $1/\pi t$ のフーリエ変換である $-\sqrt{-1}\mathrm{sgn}(f)$ との積を取り,
- 逆変換する
という操作をすればヒルベルト変換が得られます。以上をまとめると,
$$
\mathcal{H}[x](t) = \mathcal{F}^{-1}[-\sqrt{-1}\mathrm{sgn}(f)X(f)](t)
$$
ということになります。
包絡線(エンベロープ)
信号 $x(t)$ の包絡線 (エンベロープ(envelope)) は以上のヒルベルト変換によって得られた信号を用いて,
$$
\mathrm{env}_x(t) = \sqrt{x(t)^2 + (\mathcal{H}[x](t))^2}
$$
として得ることができます。
瞬時周波数
瞬時位相 (instantaneous phase) を
$$
\theta_\mathrm{inst}(t) = \arctan\frac{\mathcal{H}[x](t)}{x(t)}
$$
と定義します。信号 $x(t)$ の瞬時周波数 (instantaneous frequency) は,瞬時位相の時間微分として
$$
f_\mathrm{inst}(t) = \frac{1}{2\pi}\frac{\mathrm{d}\theta_\mathrm{inst}(t)}{\mathrm{d}t}
$$
で得られます。$1/2\pi$ のファクタは角周波数から周波数に変換するためのものです。
ヒルベルト変換の実行方法
ヒルベルト変換とそれを用いたエンベロープ,瞬時位相の抽出プログラムの実装は,pythonを使用すると簡単にかけます。
具体的には,以下のようなプログラムを作成します。
import numpy as np
import matplotlib.pyplot as plt
# from scipy import signal # scipyを使用することもできます
# テスト信号の生成
dt = 1.0e-4 #時間刻み
tms = 0.0 # 初期時間
tme = 2.0 # 終了時間
tm = np.arange(tms, tme, dt) # 時間のnumpy配列
amp = abs(np.sin(2.0*np.pi*2.0*tm)) + np.tanh(tm) # 振幅 (これが包絡線に相当する)
freq = 10.0 + 10.0*tm*tm + np.cos(2.0*np.pi*3.0*tm) # 周波数 (注意!これは瞬時周波数とは一致しません)
sig = amp*np.sin(2.0*np.pi*freq*tm) # テスト信号
# ヒルベルト変換し,包絡線と瞬時周波数を得る
jsgn = np.sign(np.fft.fftfreq(len(sig), dt))*1.0j # 1/(pi*t)のフーリエ変換のマイナス
hsig = np.fft.ifft(-jsgn*np.fft.fft(sig)) # フーリエ空間で積を取りフーリ逆変換 (畳み込み積分の計算)
env = np.sqrt(sig**2 + hsig**2) # 包絡線(エンベロープ)
phase_inst = np.arctan2(np.real(hsig), sig) # 瞬時位相
freq_inst = np.gradient(np.unwrap(phase_inst))/dt/(2.0*np.pi) # 瞬時周波数
# # scipy を使用するとき
# z = signal.hilbert(sig)
# phase_inst = np.unwrap(np.angle(z))
# freq_inst = np.gradient(phase_inst)/dt/(2.0*np.pi)
# #
# プロット
fig, (ax01, ax02) = plt.subplots(nrows=2, figsize=(6, 8))
plt.subplots_adjust(wspace=0.0, hspace=0.6)
# 入力信号と包絡線のプロット
ax01.set_xlim(tms, tme)
ax01.set_xlabel('time (s)')
ax01.set_ylabel('x')
ax01.plot(tm, sig, color='blue') # 入力信号
ax01.plot(tm, env, color='red', linestyle='dashed')
# スペクトログラムと瞬時周波数
ax02.set_xlim(tms, tme)
ax02.set_ylim(0.0, 300.0)
ax02.set_xlabel('time (s)')
ax02.plot(tm, freq_inst, color='red', linestyle='dashed')
plt.show()実際にコードを実行してみよう
上で記述したコードは hilbert-demo.pyという名前のファイルとして,好きなディレクトリ(ここでは~/Desktop/LabCode/python/hilbertとします)に保存します。
ターミナルを開き,
$ cd ~/Desktop/LabCode/python/hilbertと入力し,ディレクトリを移動します。あとは以下のコマンドで hilbert-demo.pyを実行するだけです。( $マークは無視してください)。
$ python3 hilbert-demo.py実行結果
次のようなウィンドウが立ち上がったら成功です。
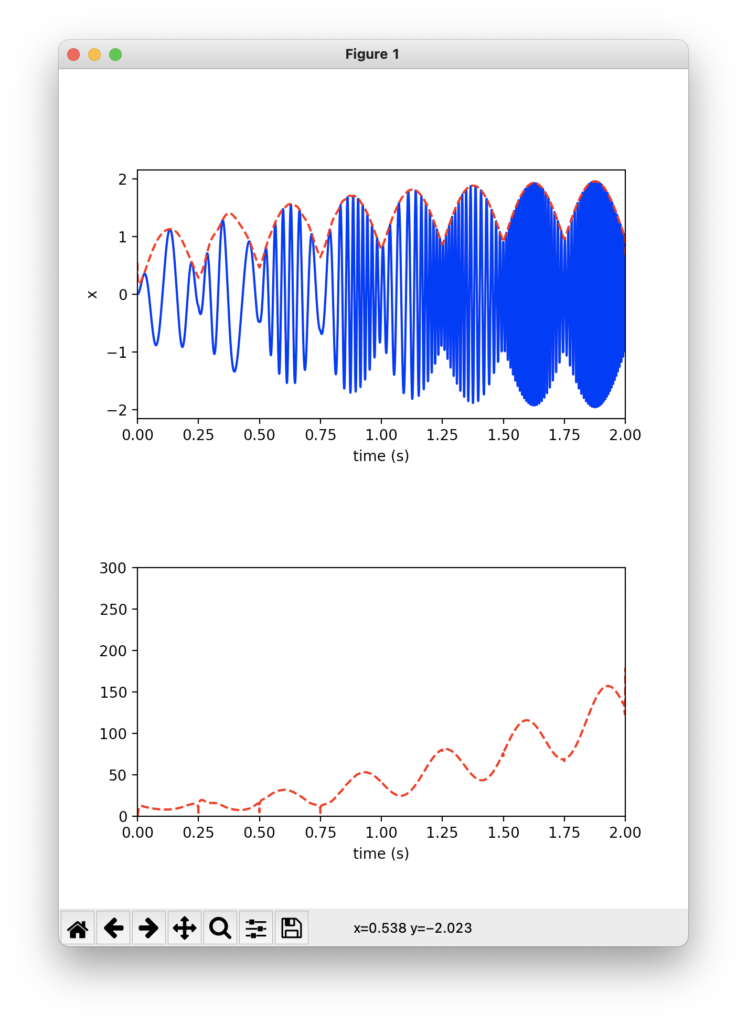
一段目の青の入力信号に対して,赤の点線で表される包絡線が抽出されていることがわかります。
下の段の瞬時周波数はわかりにくいので,STFTで解析した周波数と比較してみましょう。
STFTは前回の記事で作成したもの(の入力を今回作成したものに置き換えたもの)を使用しています。
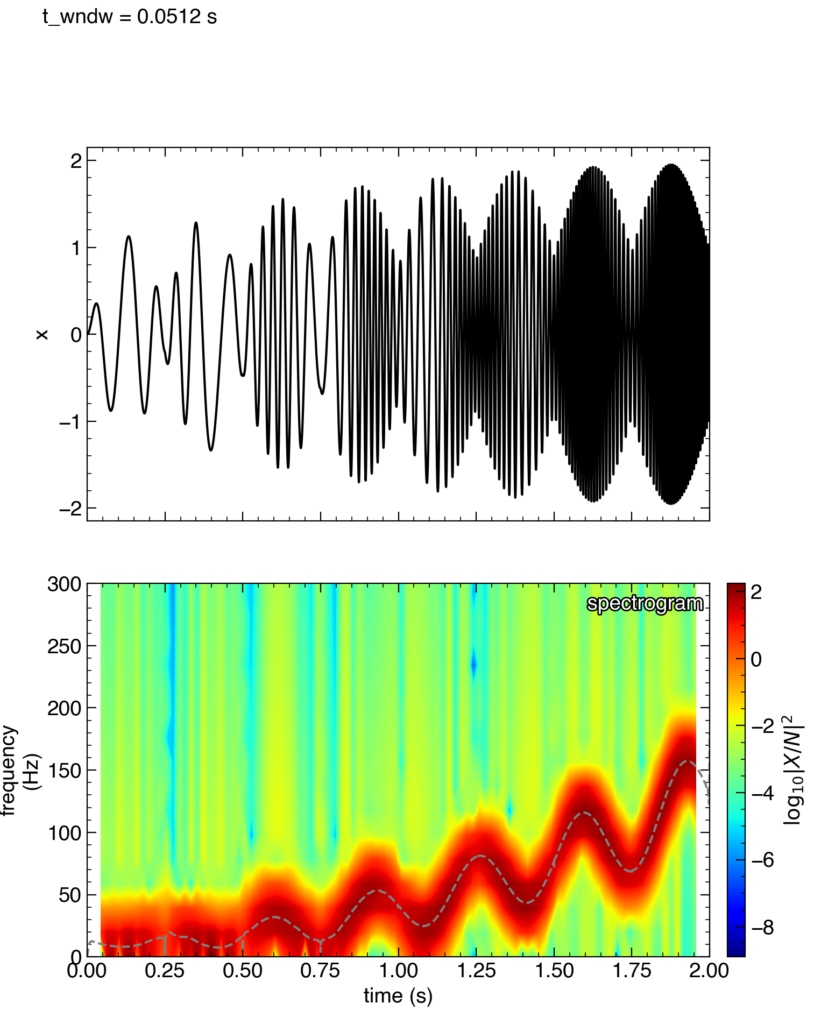
STFTで求めたスペクトログラムの赤い部分(振幅の大きい周波数成分)と,灰色の点線で表されるヒルベルト変換により求めた瞬時周波数がよく一致していることがわかります!
コードの解説
作成したコードの解説をしていきます。
import numpy as np
import matplotlib.pyplot as plt
# from scipy import signal # scipyを使用することもできます必要なモジュールをインポートします。コメントアウトしていますが,ヒルベルト変換はscipyを使用することもできます。
# テスト信号の生成
dt = 1.0e-4 #時間刻み
tms = 0.0 # 初期時間
tme = 2.0 # 終了時間
tm = np.arange(tms, tme, dt) # 時間のnumpy配列
amp = abs(np.sin(2.0*np.pi*2.0*tm)) + np.tanh(tm) # 振幅 (これが包絡線に相当する)
freq = 10.0 + 10.0*tm*tm + np.cos(2.0*np.pi*3.0*tm) # 周波数 (注意!これは瞬時周波数とは一致しません)
sig = amp*np.sin(2.0*np.pi*freq*tm) # テスト信号テスト信号を生成している部分です。今回は,振幅も周波数も時間とともに複雑に変化する波形を作って試してみました。
# ヒルベルト変換し,包絡線と瞬時周波数を得る
jsgn = np.sign(np.fft.fftfreq(len(sig), dt))*1.0j # 1/(pi*t)のフーリエ変換のマイナス
hsig = np.fft.ifft(-jsgn*np.fft.fft(sig)) # フーリエ空間で積を取りフーリ逆変換 (畳み込み積分の計算)
env = np.sqrt(sig**2 + hsig**2) # 包絡線(エンベロープ)
phase_inst = np.arctan2(np.real(hsig), sig) # 瞬時位相
freq_inst = np.gradient(np.unwrap(phase_inst))/dt/(2.0*np.pi) # 瞬時周波数
# # scipy を使用するとき
# z = signal.hilbert(sig)
# phase_inst = np.unwrap(np.angle(z))
# freq_inst = np.gradient(phase_inst)/dt/(2.0*np.pi)
# #ヒルベルト変換により,包絡線と瞬時周波数を取得します。 np.unwrap は $-\pi$ から $\pi$ にラップ(wrap) された瞬時位相をアンラップするものです。これは,たとえば,瞬時位相が $\pi$ から $\pi + \delta$ に変化した時に,$-\pi + \delta$ にジャンプさせるのではなく,本来の $\pi + \delta$ にするためのものです。これを行わないと,微分した際に $\theta_\mathrm{inst}=\pm\pi$ 付近でジャンプが現れます。
scipyを使っても解析できると述べましたが,その場合は下の部分のコメントアウトを外してください。
# プロット
fig, (ax01, ax02) = plt.subplots(nrows=2, figsize=(6, 8))
plt.subplots_adjust(wspace=0.0, hspace=0.6)
# 入力信号と包絡線のプロット
ax01.set_xlim(tms, tme)
ax01.set_xlabel('time (s)')
ax01.set_ylabel('x')
ax01.plot(tm, sig, color='blue') # 入力信号
ax01.plot(tm, env, color='red', linestyle='dashed')
# スペクトログラムと瞬時周波数
ax02.set_xlim(tms, tme)
ax02.set_ylim(0.0, 300.0)
ax02.set_xlabel('time (s)')
ax02.plot(tm, freq_inst, color='red', linestyle='dashed')
plt.show()結果をプロットします。
最後に
今回は,ヒルベルト変換を用いた包絡線と瞬時周波数の抽出方法について紹介しました。STFTも今回述べた方法も一長一短あります。解析目的や注目したい部分に合わせて,使い分けることが大切だと思います。




